
3.三角恒等式的证明要求:利用已知三角公式通过恒等变形,论证所给等式左、右相等.
2.三角函数式的化简要求:
通过对三角函数式的恒等变形使最后所得到的结果中:
①所含函数和角的名类或种类最少;②各项的次数尽可能地低;③出现的项数最少;
④一般应使分母和根号不含三角函数式;⑤对能求出具体数值的,要求出值.
1.三角函数求值问题一般有三种基本类型:
 给角求值,即在不查表的前提下,求三角函数式的值;
给角求值,即在不查表的前提下,求三角函数式的值;
 给值求值,即给出一些三角函数,而求与这些三角函数式有某种联系的三角式的值;
给值求值,即给出一些三角函数,而求与这些三角函数式有某种联系的三角式的值;
 给值求角,即给出三角函数值,求符合条件的角.
给值求角,即给出三角函数值,求符合条件的角.
 (
(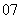 陕西)已知
陕西)已知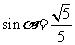 ,则
,则 的值为
的值为 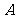
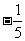
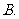
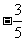
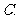
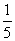
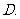
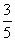
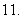 (
( 江苏)若
江苏)若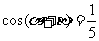 ,
,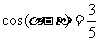 ,则
,则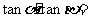
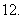 (
(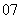 浙江)已知
浙江)已知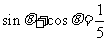 ,且
,且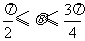 ,则
,则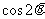 的值是
的值是
 (
(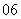 福建)已知
福建)已知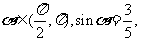 则
则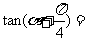
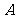
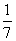
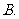
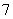
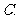
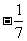
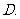

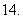 (
( 湖北)已知
湖北)已知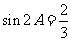 ,
,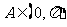 ,则
,则
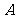
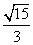
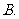
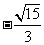
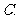
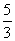
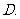
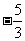
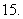 (
(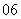 重庆文)若
重庆文)若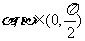 ,
,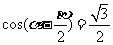 ,
,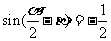 ,则
,则
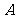
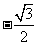
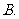
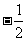
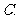
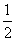
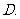
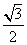
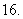 (
(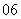 陕西)
陕西)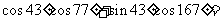
 在
在 中,
中,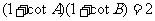 ,则
,则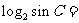
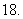 已知
已知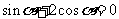 ,则
,则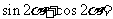
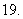 (
(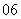 安徽文)已知
安徽文)已知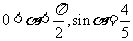 求值:
求值: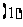
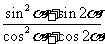 ;
;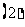
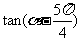
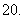 (
(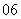 天津文)已知
天津文)已知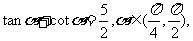 求
求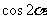 和
和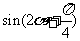 的值
的值
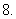 (
(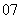 届西安地区高三八校联考)设
届西安地区高三八校联考)设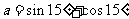 ,
, ,
,
则下列各式正确的是
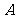
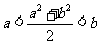
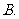
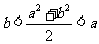
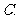
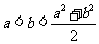
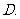
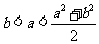
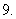 计算:
计算: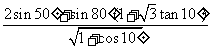
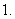 (
(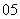 重庆文)
重庆文)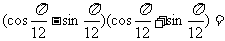
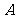
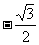
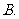
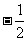
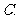
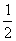
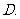
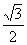
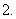 (
(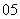 江西文)已知
江西文)已知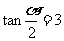 ,则
,则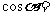
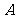
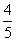
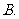
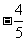
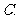
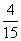
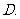

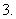 已知
已知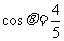 ,
,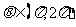 ,则
,则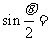
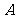
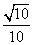
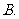
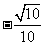
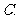
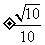
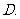
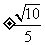
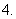 若
若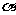 为锐角,且
为锐角,且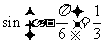 ,则
,则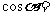
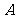
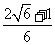
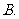
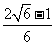
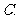
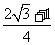
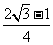
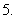 (
( 江苏)
江苏)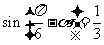 ,则
,则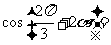
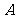
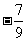
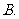
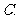
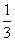
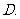
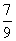
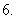 (
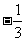
(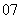 南通九校联考)已知
南通九校联考)已知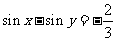 ,
, ,且
,且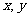 为锐角,则
为锐角,则
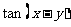 的值是
的值是 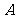
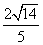
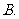
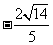
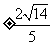
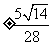
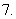 计算:
计算: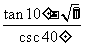
问题1.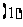 (
(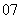 江西文)若
江西文)若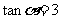 ,
,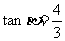 ,则
,则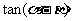 等于
等于
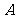

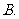

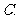
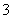
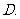
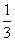
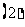 (
(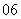 重庆)
重庆)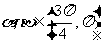 ,
,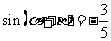 ,
,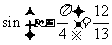 ,则
,则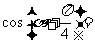
问题2.(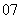 四川)已知
四川)已知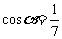 ,
,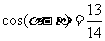 ,
,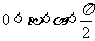 ,
,
(Ⅰ)求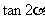 的值.(Ⅱ)求
的值.(Ⅱ)求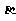 .
.
问题3.求值: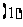
 ;
;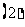
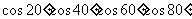
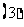 (
(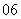 江苏)
江苏)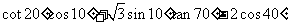
问题4.已知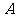 为三角形的内角,求
为三角形的内角,求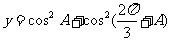 的取值范围.
的取值范围.
问题5.已知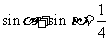 ,
, ,求值:
,求值:
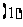
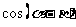 ;
;
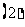
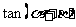
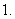 寻求所求结论中的角与已知条件中的角的关系,把握式子的变形方向,准确运用公式;
寻求所求结论中的角与已知条件中的角的关系,把握式子的变形方向,准确运用公式;
 三角变换主要体现在:函数名称的变换、角的变换、
三角变换主要体现在:函数名称的变换、角的变换、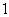 的变换、和积的变换、幂的变换等方面;
的变换、和积的变换、幂的变换等方面;
 掌握基本技巧:切割化弦,异名化同名,异角化同角等;
掌握基本技巧:切割化弦,异名化同名,异角化同角等;
 应注意的几点:
应注意的几点:
 熟悉公式的正用、逆用,还要熟练掌握公式的变形应用.
熟悉公式的正用、逆用,还要熟练掌握公式的变形应用.
 注意拆角、凑角技巧,如
注意拆角、凑角技巧,如 ,
,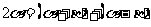 等.
等.
 注意倍角的相对性,如
注意倍角的相对性,如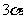 是
是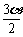 的倍角.
的倍角.
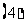 要时时注意角的范围的讨论.
要时时注意角的范围的讨论.
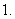 两角和与差的三角函数公式;二倍角公式;
两角和与差的三角函数公式;二倍角公式;
 降次公式:
降次公式: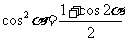 ,
,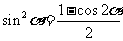 .
.
 (
(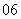 湖北文)已知
湖北文)已知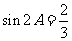 ,
,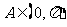 ,则
,则
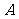
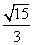
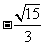
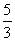
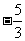
 (
(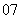 海南)若
海南)若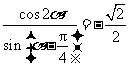 ,则
,则 的值为
的值为
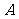
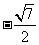
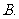
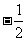
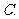
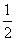
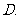
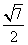
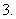 (
( 湖北文)
湖北文)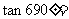
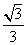
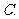
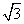
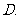
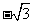
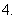 (
( 全国Ⅰ)
全国Ⅰ)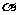 是第四象限角,
是第四象限角, ,则
,则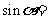
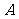
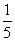
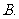
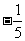
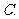
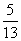
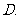
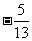
 (
( 湖南文)已知
湖南文)已知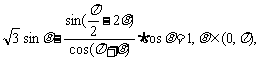 求θ的值.
求θ的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com