
2.设集合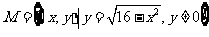 ,
,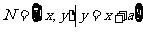 ,若
,若 ,
,
则实数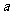 的取值范围是
的取值范围是
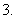 (
(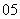 湖南十所示范性高中高三第一次联考)若
湖南十所示范性高中高三第一次联考)若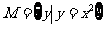 ,
,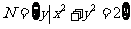
则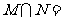 ( )
( )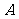

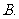
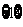
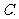
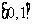
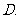

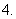 已知集合
已知集合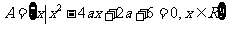 ,集合
,集合 ,若
,若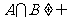 ,
,
求实数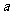 的取值范围.
的取值范围.
1.设全集为 ,在下列条件中,是
,在下列条件中,是 的充要条件的有( )
的充要条件的有( )
①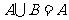 ,②
,② ,③
,③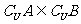 ,④
,④ ,
,
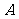
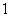 个
个 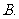
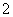 个
个 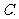
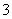 个
个 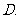
 个
个
问题1.①设全集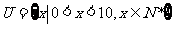 ,若
,若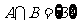 ,
, ,
,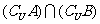
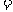
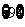 ,求
,求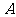 、
、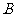
②已知集合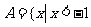 或
或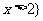 ,
,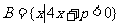 ,当
,当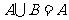 时,求
时,求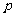 范围
范围
问题2.已知集合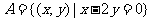 ,
,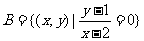 ,则
,则
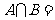 ,
,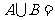
问题3.已知集合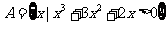 ,
,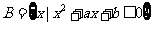 ,
,
若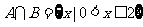 ,
, ,求实数
,求实数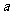 、
、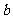 的值.
的值.
问题4.已知集合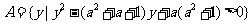 ,
,
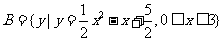 ,若
,若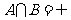 ,求实数
,求实数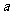 的范围.
的范围.
问题5.已知集合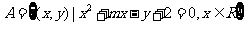 ,
,
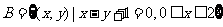 ,若
,若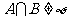 ,求实数
,求实数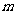 的取值范围.
的取值范围.
分析:本题的几何背景是:抛物线 与线段
与线段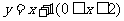 有公共点,
有公共点,
求实数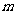 的取值范围.
的取值范围.
 求交集、并集、补集,要充分发挥数轴或文氏图的作用;
求交集、并集、补集,要充分发挥数轴或文氏图的作用;
 含参数的问题,要有分类讨论的意识,分类讨论时要防止在空集上出问题;
含参数的问题,要有分类讨论的意识,分类讨论时要防止在空集上出问题;
 集合的化简是实施运算的前提,等价转化常是顺利解题的关键.
集合的化简是实施运算的前提,等价转化常是顺利解题的关键.
 交集:
交集: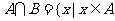 且
且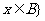 ;并集:
;并集: 或
或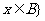 ;
;
补集:若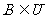 ,则
,则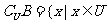 且
且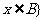 ;
;
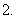
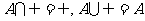 ,
,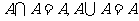 ;
;
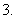
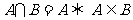 .
. ;
;
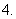
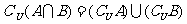 ,
,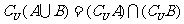 (德·摩根律)
(德·摩根律)
 (
( 安徽)已知
安徽)已知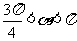 ,
,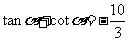
(Ⅰ)求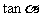 的值;
的值;
(Ⅱ)求 的值
的值
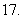 (
( 福建文)已知
福建文)已知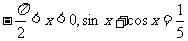 .
.
(Ⅰ)求 的值;(Ⅱ)求
的值;(Ⅱ)求 的值.
的值.
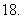 (
( 全国Ⅱ文)已知
全国Ⅱ文)已知 为第二象限的角,
为第二象限的角,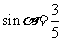 ,
,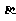 为第一象限的角,
为第一象限的角, .
.
求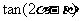 的值.
的值.
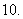
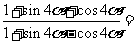
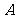
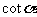 ;
;
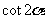 ;
;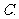
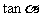 ;
;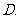
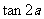
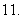 (
( 全国Ⅲ文)
全国Ⅲ文) 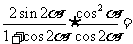
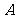
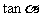 ;
;
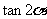 ;
;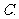
 ;
;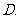
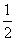
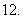
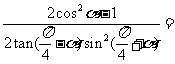
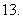 若
若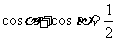 ,
,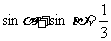 ,则
,则 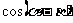 =
=
 已知
已知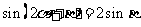 ,求证:
,求证: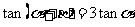
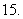 (
( 全国) 已知
全国) 已知 为锐角,且
为锐角,且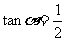 ,求
,求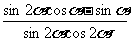 的值
的值
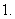 化简
化简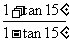 等于
等于 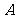
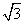

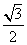
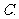
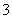
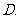

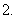

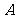
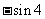

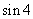
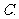
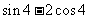
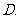

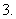 (
(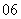 萍乡模拟)
萍乡模拟)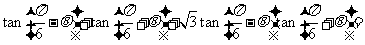
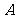
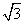


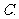
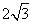
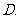
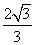
 已知
已知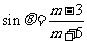 ,
,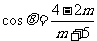 (
( ),则
),则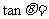
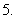

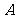


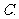

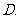
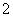

 已知
已知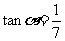 ,
,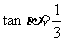 ,已知
,已知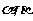 均为锐角,则
均为锐角,则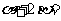
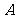
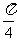

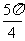
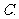
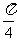 或
或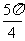
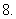 已知
已知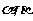 均为锐角,且满足
均为锐角,且满足 ,
,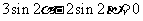 .
.
求证: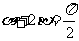
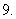 已知:
已知: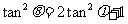 ,求证:
,求证: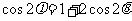
问题1.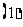 已知
已知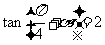 ,求
,求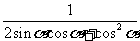 的值;
的值;
 已知
已知 ,求
,求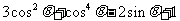 的值.
的值.
问题2.
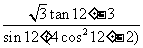 ;
;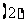
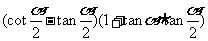 ;
;
问题3. 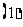 求证:
求证: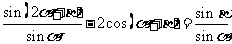 ;
;

问题4.已知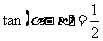 ,
,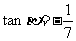 ,且
,且 ,求
,求 的值
的值
 寻求角与角之间的关系,化非特殊角为特殊角;
寻求角与角之间的关系,化非特殊角为特殊角;
 正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值;
正确灵活地运用公式,通过三角变换消去或约去一些非特殊角的三角函数值;
 一些常规技巧:“
一些常规技巧:“ ”的代换、切割化弦、和积互化、异角化同角等.
”的代换、切割化弦、和积互化、异角化同角等.
 三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角的三角函数互化.
三角函数式的化简常用方法是:异名函数化为同名三角函数,异角化为同角,异次化为同次,切割化弦,特殊值与特殊角的三角函数互化.
 三角恒等式的证明:
三角恒等式的证明:
三角恒等式包括有条件的恒等式和无条件的恒等式.
①无条件的等式证明的基本方法是化繁为简、左右归一、变更命题等,使等式两端的“异”化为“同”;②有条件的等式常用方法有:代入法、消去法、综合法、分析法等.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com