
4、(2009珠海)经过抛物线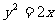 的焦点且平行于直线
的焦点且平行于直线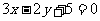 的直线
的直线 的方程是( A
)
的方程是( A
)
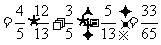
A.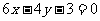 B.
B. 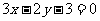
C.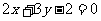 D.
D.

3、(2009广东四校)设F1、F2为曲线C1: + =1的焦点,P是曲线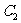 :
: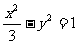 与C1的一个交点,则△PF1F2的面积为( )C
与C1的一个交点,则△PF1F2的面积为( )C
(A) (B) 1 (C) (D) 2
2、(2009吴川)若圆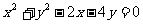 的圆心到直线
的圆心到直线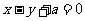 的距离为
的距离为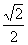 ,则a的值为(
)C
,则a的值为(
)C
A.-2或2 B.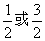 C.2或0 D.-2或0
C.2或0 D.-2或0
1、(2009揭阳)若点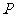 到直线
到直线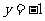 的距离比它到点
的距离比它到点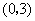 的距离小2,则点
的距离小2,则点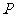 的轨迹方程为( )A
的轨迹方程为( )A
A. 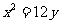 B.
B.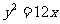 C.
C.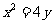 D.
D.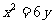
9、(2009广州)已知:A、B、C是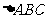 的内角,
的内角,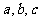 分别是其对边长,向量
分别是其对边长,向量 ,
,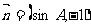 ,
,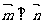 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若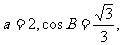 求
求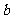 的长.
的长.
解:(Ⅰ)
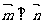
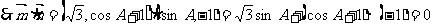
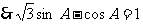 ……4分
……4分
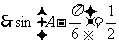 ……6分
……6分
∵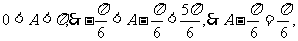 ……7分
……7分
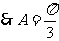 .……8分
.……8分
(Ⅱ)在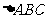 中,
中,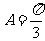 ,
,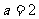 ,
,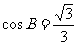
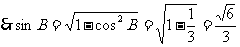 ……9分
……9分
由正弦定理知: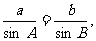 ……10分
……10分
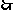
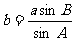 =
=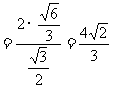 .
.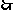
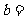
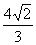 ……12分
……12分
8、(2009广东六校)设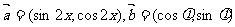
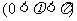 ,函数
,函数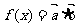 且
且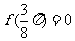 .
.
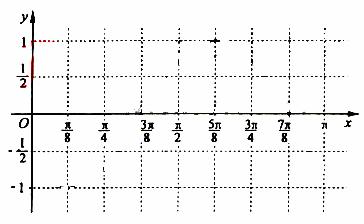
(Ⅰ)求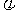 ;(Ⅱ)在给出的直角坐标系中画出函数
;(Ⅱ)在给出的直角坐标系中画出函数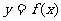 在区间
在区间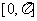 上的图像;
上的图像;
(Ⅲ)根据画出的图象写出函数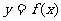 在
在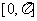 上的单调区间和最值.
上的单调区间和最值.
解: 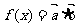 =
=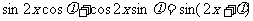 2分
2分
由题可知: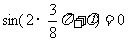 ,
3分
,
3分
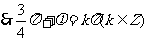 ,
4分
,
4分
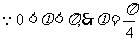 5分
5分
(2)
9分
(3)单调增区间: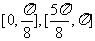 10分
10分
单调减区间: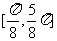 11分
11分
函数的最大值是:1
函数的最小值是: 12分
12分
7、(2009饶平)已知向量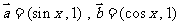 。
。
(1) 当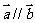 时,求
时,求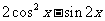 的值;
的值;
(2) 求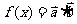 的最小正周期。
的最小正周期。
解:(1)
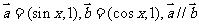 ,∴
,∴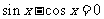 …..3分
…..3分
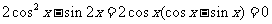 。…………………6分
。…………………6分
(2)由已知可得: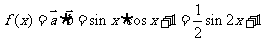 ………..11分
………..11分
∴ f(x)的最小正周期为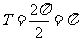 …………12分
…………12分
6、(2009中山)已知向量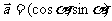 ,
, 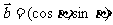 ,
, 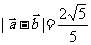 .
.
(Ⅰ)求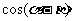 的值;
的值;
(Ⅱ)若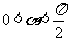 ,
, 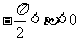 , 且
, 且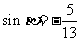 , 求
, 求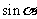 .
.
解:(Ⅰ)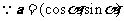 ,
, 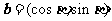 ,
,
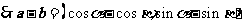 . ……………2分
. ……………2分
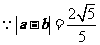 ,
, 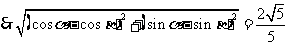 , ………3分
, ………3分
即 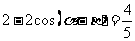 , ………5分
, ………5分 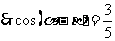 . ……………6分
. ……………6分
(Ⅱ)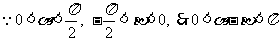 , ……………7分
, ……………7分
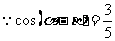 ,
, 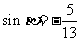
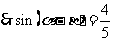 ,
, 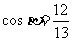 ……………9分
……………9分 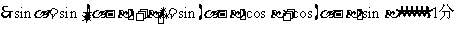
 . ……………12分
. ……………12分
5、(2009潮州)函数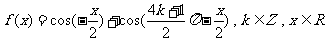 。
。
(1)求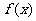 的周期;(2)解析式及
的周期;(2)解析式及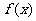 在
在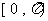 上的减区间;
上的减区间;
(3)若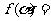
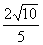 ,
,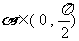 ,求
,求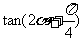 的值。
的值。
解:(1)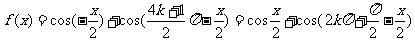
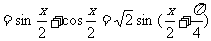 ,(
,(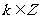 )
)
所以,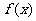 的周期
的周期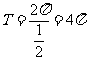 。 …… 4分
。 …… 4分
(2)由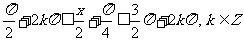 ,得
,得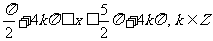 。
。
又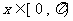 ,
,
令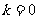 ,得
,得
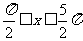 ;令
;令 ,得
,得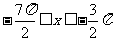 (舍去)
(舍去)
∴
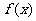 在
在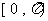 上的减区间是
上的减区间是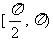 。 …… 8分
。 …… 8分
(3)由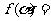
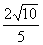 ,得
,得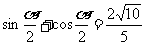 ,
,
∴ 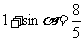 , ∴
, ∴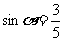
又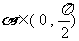 ,∴
,∴
∴ 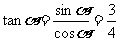 ,∴
,∴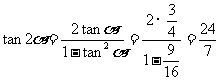
∴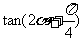
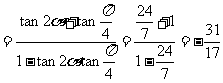 。
……12分
。
……12分
4、(2009珠海)已知函数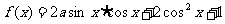 ,
,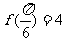 ,
,
(1)求实数a的值;
(2)求函数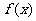 在
在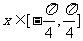 的值域。
的值域。
解: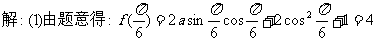 ,
,
即: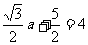 ,………………………..2分
,………………………..2分
解得: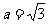 ;
;
 。……………………………..3分
。……………………………..3分
(2)由(1)得: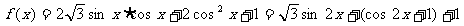
……………….…..5分
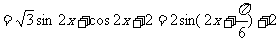 ………….…………7分
………….…………7分
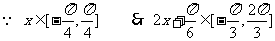 ,…………………………………………..8分
,…………………………………………..8分
令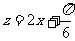 ,则
,则 ,…10分
,…10分
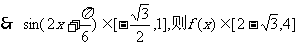 ,
,
即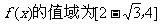 …………………………….12分
…………………………….12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com