
4、解:(1)由已知得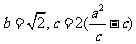 ,解得:
,解得: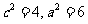 ……………………2分
……………………2分
所求椭圆方程为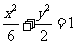 ………………………………………………4分
………………………………………………4分
(2)因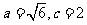 ,得
,得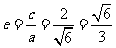 ……………………………………7分
……………………………………7分
(3)因点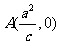 即A(3,0),设直线PQ方程为
即A(3,0),设直线PQ方程为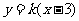 ………………8分
………………8分
则由方程组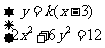 ,消去y得:
,消去y得: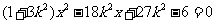
设点 则
则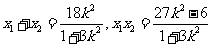 ……………………10分
……………………10分
因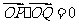 ,得
,得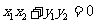 ,
,
又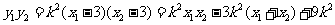 ,代入上式得
,代入上式得
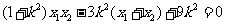 ,故
,故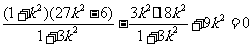
解得: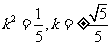 ,所求直线PQ方程为
,所求直线PQ方程为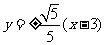 ……………………14分
……………………14分
3、解:(1)由已知,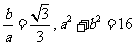 ,…………………2分
,…………………2分
解得: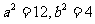 ,
…………………4分
,
…………………4分
 所以椭圆
所以椭圆 的方程是:
的方程是: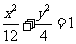 .
…………………5分
.
…………………5分
(2)解法1:设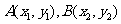
由题意得: 直线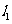 的方程为:
的方程为: 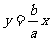 ,直线
,直线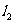 的方程为:
的方程为: 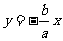 ,………………7分
,………………7分
则直线 的方程为:
的方程为: 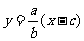 ,其中点
,其中点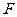 的坐标为
的坐标为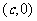 ; ………………………8分
; ………………………8分
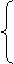
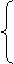 由
由 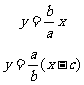 得:
得: 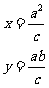 ,则点
,则点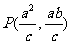 ; ………9分
; ………9分
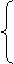 由
由 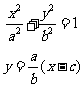 消y得:
消y得: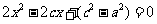 ,则
,则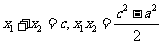 ; 10分
; 10分
由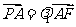 得:
得: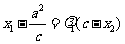 ,则:
,则: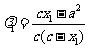 ,
,
同理由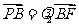 得:
得: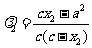 , …………………………………………………12分
, …………………………………………………12分
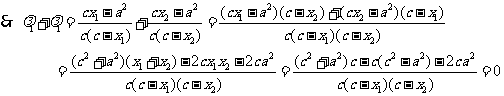
故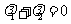 为常数. ……………………………………………………………………14分
为常数. ……………………………………………………………………14分
解法2:过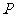 作
作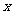 轴的垂线
轴的垂线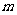 ,过
,过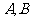 分别作
分别作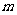 的垂线,垂足分别为
的垂线,垂足分别为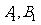 ,…6分
,…6分
由题意得: 直线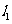 的方程为:
的方程为: 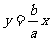 ,直线
,直线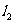 的方程为:
的方程为: 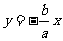 ,………………8分
,………………8分
则直线 的方程为:
的方程为: 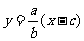 ,其中点
,其中点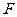 的坐标为
的坐标为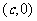 ; ………………………9分
; ………………………9分
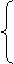
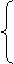 由
由 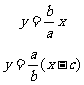 得:
得: 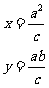 ,则直线m为椭圆E的右准线; ………10分
,则直线m为椭圆E的右准线; ………10分
则: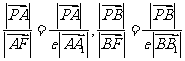 ,其中e的离心率; …………………………12分
,其中e的离心率; …………………………12分
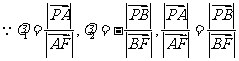 ,
,
故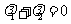 为常数. ………………………………………………………………14分
为常数. ………………………………………………………………14分
2、解:(1)依题意,设椭圆方程为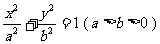 ,则其右焦点坐标为
,则其右焦点坐标为
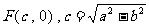 ,
………… 2分
,
………… 2分
由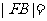
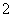 ,得
,得 ,
,
即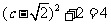 ,解得
,解得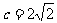 。
………… 4分
。
………… 4分
又
∵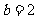 ,∴
,∴  ,即椭圆方程为
,即椭圆方程为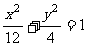 。 ……5分
。 ……5分
(2)由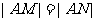 知点
知点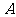 在线段
在线段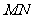 的垂直平分线上,
的垂直平分线上,
由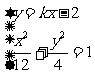 消去
消去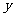 得
得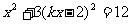
即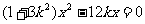 (*) ………… 7分
(*) ………… 7分
由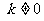 ,得方程(*)的
,得方程(*)的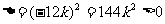 ,即方程(*)有两个不相等的实数根。
,即方程(*)有两个不相等的实数根。
…………8分
设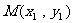 、
、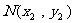 ,线段
,线段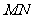 的中点
的中点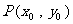 ,
,
则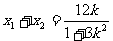 ,
,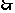
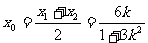 ,
,
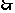
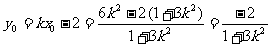 ,即
,即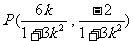 ……… 10分
……… 10分
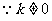 ,∴直线
,∴直线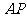 的斜率为
的斜率为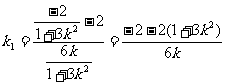 ,……11分
,……11分
由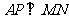 ,得
,得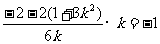 , …… 12分
, …… 12分
∴
 ,解得:
,解得: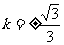 ,即
,即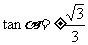 , …… 13分
, …… 13分
又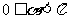 ,故
,故 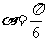 ,或
,或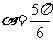 ,
,
∴ 存在直线 满足题意,其倾斜角
满足题意,其倾斜角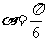 ,或
,或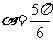 。…… 14分
。…… 14分
1、解:(1)当
 时,∵
时,∵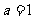 ,∴
,∴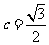 ,
,
∴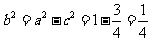 ,
,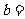
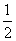 ,点
,点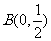 ,
,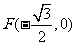 ,
,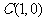 ---------2分
---------2分
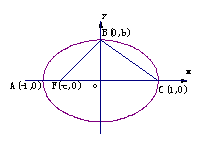 设
设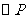 的方程为
的方程为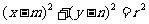
由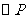 过点F,B,C得
过点F,B,C得
∴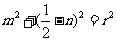 -----------------①
-----------------①
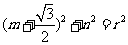 -----------------②
-----------------②
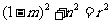 -------------------③----------------------------5分
-------------------③----------------------------5分
由①②③联立解得
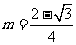 ,
,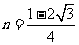 ,
,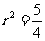 -----------------------7分
-----------------------7分
∴所求的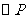 的方程为
的方程为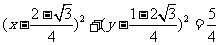 -------------8分
-------------8分
(2)∵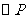 过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为
过点F,B,C三点,∴圆心P既在FC的垂直平分线上,也在BC的垂直平分线上,FC的垂直平分线方程为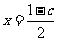 --------④----------------------9分
--------④----------------------9分
∵BC的中点为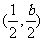 ,
,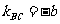
∴BC的垂直平分线方程为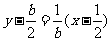 -----⑤---------------------10分
-----⑤---------------------10分
由④⑤得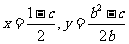 ,即
,即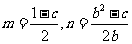 ----------------11分
----------------11分
∵P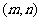 在直线
在直线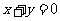 上,∴
上,∴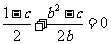

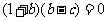
∵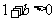 ∴
∴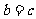 由
由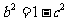 得
得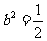
∴椭圆的方程为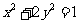 --------------------------------------------------------------14分
--------------------------------------------------------------14分
12、(2009广东五校)设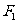 、
、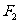 分别是椭圆
分别是椭圆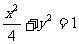 的左、右焦点.
的左、右焦点.
(Ⅰ)若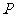 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求
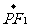 ·
·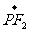 的最大值和最小值;
的最大值和最小值;
(Ⅱ)设过定点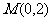 的直线
的直线 与椭圆交于不同的两点
与椭圆交于不同的两点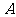 、
、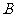 ,求直线
,求直线 的斜率
的斜率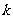 的取值范围.
的取值范围.
祥细答案
11、(2009中山一中)已知动圆过定点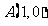 ,且与直线
,且与直线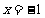 相切.
相切.
(1) 求动圆的圆心轨迹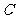 的方程;
的方程;
(2) 是否存在直线 ,使
,使 过点
过点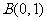 ,并与轨迹
,并与轨迹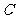 交于
交于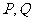 两点,
两点,
且满足 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
10、(2009朝阳一中)设椭圆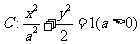 的左右焦点分别为
的左右焦点分别为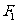 、
、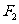 ,
,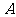 是椭圆
是椭圆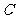 上的一点,且
上的一点,且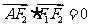 ,坐标原点
,坐标原点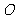 到直线
到直线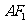 的距离为
的距离为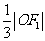 .
.
(Ⅰ)求椭圆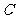 的方程;
的方程;
(Ⅱ)设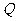 是椭圆
是椭圆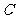 上的一点,过点
上的一点,过点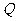 的直线
的直线 交
交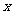 轴于点
轴于点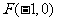 ,交
,交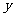 轴于点
轴于点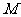 ,若
,若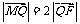 ,求直线
,求直线 的斜率.
的斜率.
9、(2009广东六校一)已知点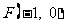 和直线
和直线 :
: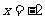 ,动点
,动点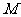 到点
到点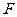 的距离与到直线
的距离与到直线 的距离之比为
的距离之比为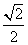 .
.
(I)求动点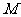 的轨迹方程;
的轨迹方程;
 (II)设过点F的直线交动点
(II)设过点F的直线交动点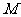 的轨迹于A、B两点,并且线段AB的中点在直线
的轨迹于A、B两点,并且线段AB的中点在直线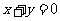 上,求直线AB的方程.
上,求直线AB的方程.
8、(2009金山)已知曲线C:xy=1,过C上一点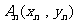 作一斜率为
作一斜率为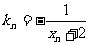 的直线交曲线C于另一点
的直线交曲线C于另一点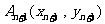 ,点列
,点列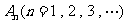 的横坐标构成数列{
的横坐标构成数列{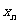 },其中
},其中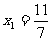 .
.
(1)求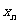 与
与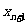 的关系式;(2)求证:{
的关系式;(2)求证:{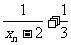 }是等比数列;
}是等比数列;
(3)求证: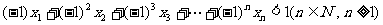 。
。
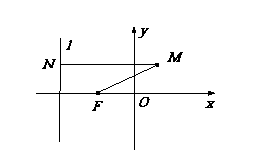
7、(2009金山)已知A、B分别是椭圆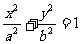 的左右两个焦点,O为坐标原点,点P
的左右两个焦点,O为坐标原点,点P )在椭圆上,线段PB与y轴的交点M为线段PB的中点。
)在椭圆上,线段PB与y轴的交点M为线段PB的中点。
(1)求椭圆的标准方程;
(2)点C是椭圆上异于长轴端点的任意一点,对于△ABC,求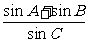 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com