
3、(2009广东五校)通过研究学生的学习行为,专家发现,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的兴趣激增;中间有一段时间,学生的兴趣保持较理想的状态,随后学生的注意力开始分散,设f (t)表示学生注意力随时间t(分钟)的变化规律(f(t)越大,表明学生注意力越集中),经过实验分析得知:
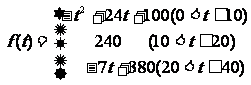
(1)讲课开始后多少分钟,学生的注意力最集中?能持续多少分钟?
(2)讲课开始后5分钟与讲课开始后25分钟比较,何时学生的注意力更集中?
(3)一道数学难题,需要讲解24分钟,并且要求学生的注意力至少达到180,那么经过适当安排,老师能否在学生达到所需的状态下讲授完这道题目?
解:(1)当 ,
,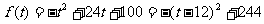 是增函数…1分,
是增函数…1分,
且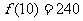 …………2分;
…………2分;
 ,
,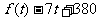 是减函数,且
是减函数,且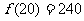 …………4分.
…………4分.
所以,讲课开始10分钟,学生的注意力最集中,能持续10分钟…………5分.
(2)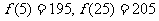 …………7分,
…………7分,
故讲课开始25分钟时,学生的注意力比讲课开始后5分钟更集中…………9分.
(3)当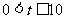 时,
时,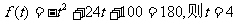 …………11分;
…………11分;
当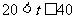 ,令
,令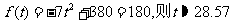 …………12分,
…………12分,
则学生注意力在180以上所持续的时间28.57-4=24.57>24…………13分,
所以,经过适当安排,老师可以在学生达到所需要的状态下讲授完这道题…………14分.
2、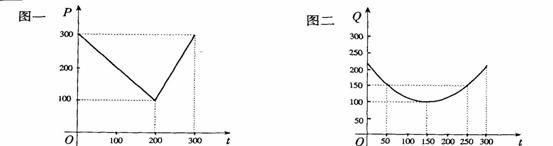 (2009执信)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(2009执信)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图一的一条折线表示;西红柿的种植成本与上市时间的关系用图二的抛物线段表示.
(Ⅰ) 写出图一表示的市场售价与时间的函数关系式P=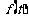 ;
;
写出图二表示的种植成本与时间的函数关系式Q=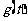 ;
;
(Ⅱ) 认定市场售价减去种植成本为纯收益,问何时上市的西红柿收益最大?
(注:市场售价和种植成本的单位:元/ kg,时间单位:天)
kg,时间单位:天)
解:(Ⅰ)由图一可得市场售价与时间的函数关系为
f(t)=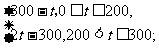
由图二可得种植成本与时间的函数关系为g(t)=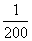 (t-150)2+100,0≤t≤300.
(t-150)2+100,0≤t≤300.
(Ⅱ)设t时刻的纯收益为h(t),则由题意得h(t)=f(t)-g(t)
即h(t)=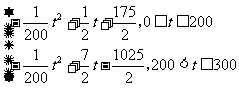
当0≤t≤200时,配方整理得h(t)=-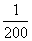 (t-50)2+100,
(t-50)2+100,
所以,当t=50时,h(t)取得区间[0,200]上的最大值100;
当200<t≤300时,配方整理得h(t)=-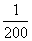 (t-350)2+100
(t-350)2+100
所以,当t=300时,h(t)取得区间[200,300]上的最大值87.5.
综上,由100>87.5可知,h(t)在区间[0,300]上可以取得最大值100,此时t=50,即从二月一日开始的第50天时,上市的西红柿纯收益最大.
1、(2009广州六中)已知二次函数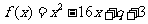 :
:
⑴若函数在区间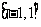 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围;
⑵问:是否存在常数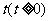 ,当
,当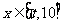 时,
时,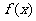 的值域为区间
的值域为区间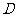 ,且
,且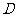 的长度为
的长度为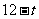 。
。
解:⑴ ∵二次函数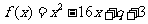 的对称轴是
的对称轴是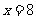
∴函数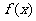 在区间
在区间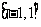 上单调递减
上单调递减
∴要函数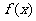 在区间
在区间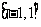 上存在零点须满足
上存在零点须满足
即 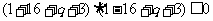 解得
解得
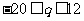
⑵ 当 时,即
时,即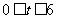 时,
时,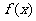 的值域为:
的值域为: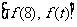 ,
,
即
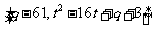
∴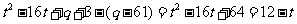
∴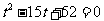 ∴
∴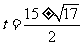 ,经检验
,经检验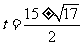 不合题意,舍去。
不合题意,舍去。
当 时,即
时,即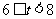 时,
时,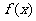 的值域为:
的值域为: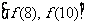 ,即
,即 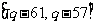
∴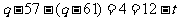 ∴
∴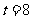
经检验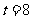 不合题意,舍去。
不合题意,舍去。
当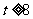 时,
时,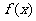 的值域为:
的值域为: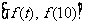 ,即
,即 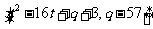
∴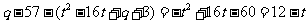
∴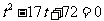 ∴
∴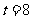 或
或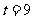
经检验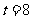 或
或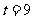 满足题意,所以存在常数
满足题意,所以存在常数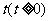 ,当
,当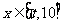 时,
时,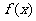 的值域为区间
的值域为区间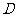 ,且
,且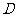 的长度为
的长度为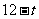 。
。
8、(2009潮州)为了保证信息安全传输必须使用加密方式,有一种方式其加密、解密原理如下:
|
|
|


 明文
密文
密文
明文
明文
密文
密文
明文
已知加密为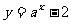
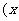 为明文、
为明文、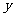 为密文
为密文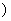 ,如果明文“
,如果明文“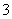 ”通过加密后得到密文为“
”通过加密后得到密文为“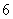 ”,
”,
再发送,接受方通过解密得到明文“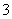 ”,若接受方接到密文为“
”,若接受方接到密文为“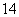 ”,则原发的明文
”,则原发的明文
是 。
解:依题意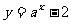 中,当
中,当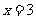 时,
时,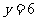 ,故
,故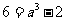 ,解得
,解得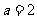 ,所以加密为
,所以加密为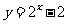 ,因此,当
,因此,当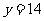 时,由
时,由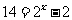 ,解得
,解得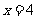 。
。
7、(广东五校第一次)函数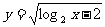 的定义域为_____________。
的定义域为_____________。
6、(2009高州中学)函数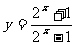 的值域是
;
的值域是
;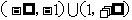
5、(2009高州中学)经化简后,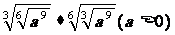 的结果是
,
的结果是
,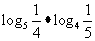 的结果是
;
的结果是
;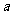 ;1
;1
4、(2009深圳外国语学校)函数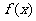 对于任意实数
对于任意实数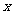 满足条件
满足条件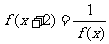 ,若
,若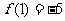 ,则
,则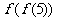 =
。
=
。
由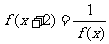 得
得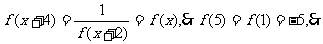
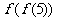
=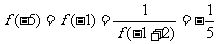 。
。
3、(2009金山中学)已知函数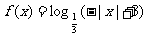 定义域是
定义域是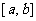
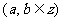 ,值域是
,值域是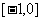 ,则满足条件的整数对
,则满足条件的整数对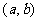 有 对。5
有 对。5
2、(2009执信)函数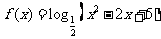 的值域是__________ .
的值域是__________ . 
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com