
7.(2009湖南卷文)如图2,两块斜边长相等的直角三角板拼在一起,若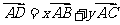 ,则
,则 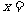
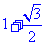 ,
,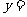
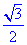 .
.
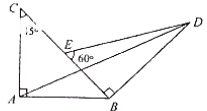
图2
解:作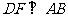 ,设
,设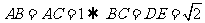 ,
,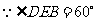 ,
,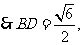
由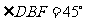 解得
解得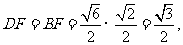 故
故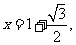
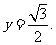
6.(2009江西卷理)已知向量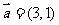 ,
,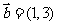 ,
,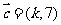 ,若
,若 ∥
∥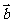 ,则
,则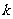 =
.
=
.
答案: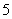
[解析]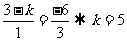
5.(2009江西卷文)已知向量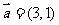 ,
,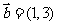 ,
, 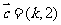 ,若
,若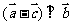 则
则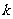 =
.
=
.
答案: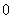
[解析]因为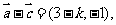 所以
所以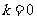 .
.
4.(2009安徽卷文)在平行四边形ABCD中,E和F分别是边CD和BC的中点,或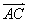 =
=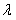
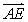 +
+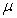
 ,其中
,其中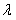 ,
,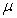
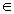 R ,则
R ,则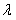 +
+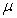 = _________。21世纪教育网
= _________。21世纪教育网 

[解析]设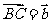 、
、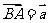 则
则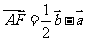 ,
,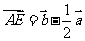 ,
,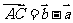
代入条件得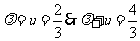
[答案]4/3
3.(2009安徽卷理)给定两个长度为1的平面向量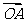 和
和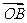 ,它们的夹角为
,它们的夹角为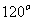 .
.
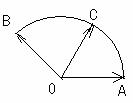 如图所示,点C在以O为圆心的圆弧
如图所示,点C在以O为圆心的圆弧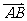 上变动.
上变动.
若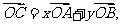 其中
其中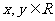 ,则
,则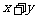
的最大值是________.
[解析]设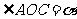
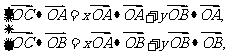 ,即
,即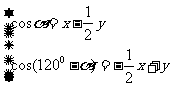
∴
2.(2009江苏卷)已知向量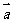 和向量
和向量 的夹角为
的夹角为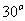 ,
,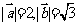 ,则向量
,则向量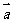 和向量
和向量 的数量积
的数量积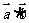 = 。
= 。
[解析] 考查数量积的运算。 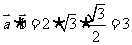
1.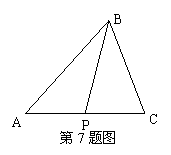 (2009广东卷理)若平面向量
(2009广东卷理)若平面向量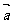 ,
,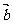 满足
满足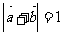 ,
,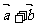 平行于
平行于 轴,
轴,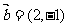 ,则
,则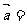 .
. 

[解析]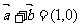 或
或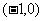 ,则
,则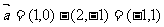
或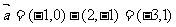 .
.
24.(2009重庆卷文)已知向量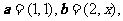 若
若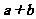 与
与 平行,则实数
平行,则实数 的值是( )
的值是( )
A.-2 B.0 C.1 D.2
[答案]D
解法1因为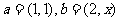 ,所以
,所以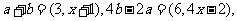 由于
由于 与
与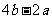 平行,得
平行,得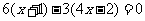 ,解得
,解得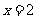 。
。
解法2因为 与
与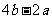 平行,则存在常数
平行,则存在常数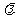 ,使
,使 ,即
,即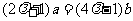 ,根据向量共线的条件知,向量
,根据向量共线的条件知,向量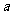 与
与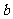 共线,故
共线,故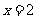 。
。
23.(2009重庆卷理)已知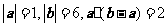 ,则向量
,则向量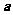 与向量
与向量 的夹角是( )
的夹角是( )
A.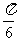 B.
B.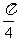 C.
C.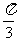 D.
D.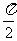


[答案]C
[解析]因为由条件得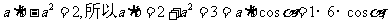
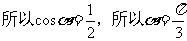
22.(2009福建卷文)设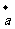 ,
,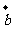 ,
, 为同一平面内具有相同起点的任意三个非零向量,且满足
为同一平面内具有相同起点的任意三个非零向量,且满足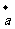 与
与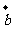 不共线,
不共线,
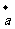
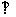
 ∣
∣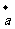 ∣=∣
∣=∣ ∣,则∣
∣,则∣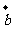 •
• ∣的值一定等于
∣的值一定等于 

A.以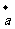 ,
,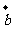 为邻边的平行四边形的面积
B. 以
为邻边的平行四边形的面积
B. 以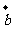 ,
, 为两边的三角形面积
为两边的三角形面积
C.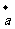 ,
,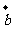 为两边的三角形面积
D. 以
为两边的三角形面积
D. 以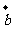 ,
, 为邻边的平行四边形的面积
为邻边的平行四边形的面积
解析 假设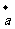 与
与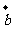 的夹角为
的夹角为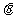 ,∣
,∣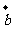 •
• ∣=︱
∣=︱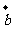 ︱·︱
︱·︱ ︱·∣cos<
︱·∣cos<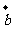 ,
, >∣=︱
>∣=︱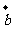 ︱·︱
︱·︱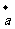 ︱•∣cos(90
︱•∣cos(90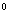

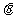 )∣=︱
)∣=︱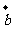 ︱·︱
︱·︱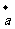 ︱•sin
︱•sin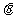 ,即为以
,即为以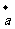 ,
,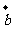 为邻边的平行四边形的面积,故选A。
为邻边的平行四边形的面积,故选A。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com