
7.从编号为1,2,3,4,5,6,7,8,9,10的十个球中,任取5个球,则这5个球编号之和为奇数的概率是__ ______.
______.
6.有3人,每人都以相同的概率被分配到4个房间中的一间,则至少有2人分配到同一房间的概率是__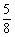 ______.
______.
5.一批产品共10件,其中有两件次品,现随机地抽取5件,则所取5件中至多有一件次品的概率为B
A.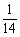 B.
B.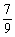 C.
C. D.
D.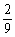
4.从装有2个红球和2个白球的口袋内任取2个球,那么互斥而不对立的两个事件是C
A.至少有1个白球,都是红球 B.至少有1个白球,至多有1个红球
C.恰有1个白球,恰有2个白球 D.至多有1个白球,都是红球
3.甲、乙两人下棋,甲获胜的概率是40%,甲不输的概率为90%,则甲、乙二人下成和棋的概率为D
A.60% B.30% C.10% D.50%
2.从一批羽毛球产品中任取一个,质量小于4.8 g的概率是0.3,质量不小于4.85 g的概率是0.32,那么质量在[4.8,4.85)g范围内的概率是B
A.0.62 B.0.38 C.0.7 D.0.68
1.两个事件互斥是这两个事件对立的B
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
[例1]
今有标号为1,2,3,4,5的五封信,另有同样标号的五个信封.现将五封信任意地装入五个信封,每个信封装入一封信,试求至少有两封信配对的概率. 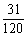
思考讨论
若求(1)至少有1封信配对. 答案: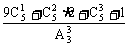 .
.
(2)没有一封信配对. 答案:1-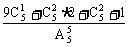 .
.
[例2] (2004年合肥模拟题)在袋中装20个小球,其中彩球有n个红色、5个蓝色、10个黄色,其余为白球.
求:(1)如果从袋中取出3个都是相同颜色彩球(无白色)的概率是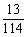 ,且n≥2,那么,袋中的红球共有几个? n=2.
,且n≥2,那么,袋中的红球共有几个? n=2.
(2)根据(1)的结论,计算从袋中任取3个小球至少有一个是红球的概率. 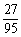
[例3] 9个国家乒乓球队中有3个亚洲国家队,抽签分成甲、乙、丙三组(每组3队)进行预赛,试求:
(1)三个组各有一个亚洲队的概率;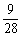
(2)至少有两个亚洲队分在同一组的概率. 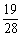
[例4](福建卷)甲、乙两人在罚球线投球命中的概率分别为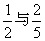 .
.
(Ⅰ)甲、乙两人在罚球线各投球一次,求恰好命中一次的概率;
(Ⅱ)甲、乙两人在罚球线各投球二次,求这四次投球中至少一次命中的概率.
[例5](北京卷)甲、乙两人各进行3次射击,甲每次击中目标的概率为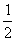 ,乙每次击中目标的概率
,乙每次击中目标的概率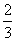 ,
,
(I)甲恰好击中目标的2次的概率;
(II)乙至少击中目标2次的概率;
(III)求乙恰好比甲多击中目标2次的概率.
[例6] 某单位一辆交通车载有8个职工从单位出发送他们下班回家,途中共有甲、乙、丙3个停车点,如果某停车点无人下车,那么该车在这个点就不停车.假设每个职工在每个停车点下车的可能性都是相等的,求下列事件的概率:
(1)该车在某停车点停车;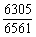
(2)停车的次数不少于2次;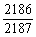
(3)恰好停车2次. 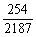
〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓〓
2.有10张人民币,其中伍元的有2张,贰元的有3张,壹元的有5张,从中任取3张,则3张中至少有2张的币值相同的概率为_____ ___.
___.
1.(2004年东北三校模拟题)一个口袋中装有大小相同的2个白球和3个黑球,从中摸出一个球,放回后再摸出一个球,则两次摸出的球恰好颜色不同的概率为__ ______.
______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com