
6、一棱锥被平行于底面的平面所截,若截面面积与底面面积之比为1:3,则此截面把一条侧棱分成的两线段之比为( )
A、1:3
B、1:2
C、1: D、1:
D、1: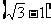
5、若一个三棱锥中,有一条棱长为a,其余棱长均为1,则其体积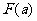 取得最大值时
取得最大值时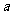 的值为( )
的值为( )
A、1
B、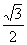 C、
C、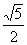 D、
D、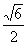
4、若P是正四面体内一点,P到各面距离之和是一个定值,这个定值等于( )
A、正四面体的棱长 B、正四面体的斜高
C、正四面体相对棱间的距离 D、正四面体的高
2.如果三棱锥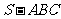 的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点
的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点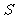 在底面的射影
在底面的射影 在
在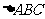 内,那么
内,那么 是
是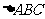 的( )
的( )
 垂心
垂心  重心
重心  外心
外心  内心
内心
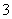 .已知三棱锥
.已知三棱锥 的三个侧面与底面全等,且
的三个侧面与底面全等,且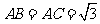 ,
,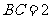 ,则以
,则以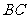 为棱,以面
为棱,以面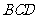 与面
与面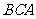 为面的二面角的大小是( )
为面的二面角的大小是( )
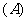
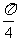
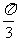
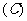
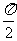
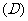
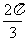
1.给出下列命题:
①底面是正多边形的棱锥是正棱锥;
②侧棱都相等的棱锥是正棱锥;
③侧棱和底面成等角的棱锥是正棱锥;
④侧面和底面所成二面角都相等的棱锥是正棱锥,其中正确命题的个数是( )

例1.正四棱锥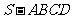 中,高
中,高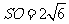 ,两相邻侧面所成角为
,两相邻侧面所成角为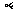 ,
,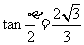 ,
,
(1)求侧棱与底面所成的角。(2)求侧棱 长、底面边长和斜高(见图)。
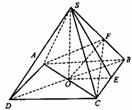
解:(1)
作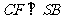 于
于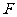 ,连结
,连结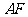 ,则
,则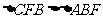 且
且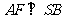 ,故
,故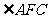 是相邻侧面所成二面角的平面角,连结
是相邻侧面所成二面角的平面角,连结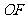 ,则
,则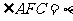 ,
, 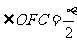 ,在
,在 与
与 中,
中, 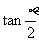 =
=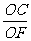 =
=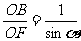 (其中
(其中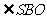 为
为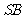 与底面所成的角,设为
与底面所成的角,设为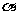 ) 故
) 故 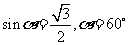 。
。
(2)在
 中,侧棱
中,侧棱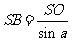 =
= ,
,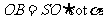
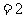
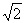 ,
,
∴边长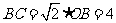 ;取
;取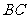 的中点
的中点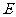 ,连结
,连结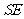 ,则
,则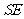 是正四棱锥的斜高,
是正四棱锥的斜高,
在 中,斜高
中,斜高
 ;
;
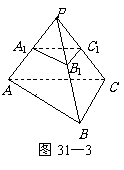
 例2.如图正三棱锥
例2.如图正三棱锥 中,底面边长为
中,底面边长为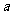 ,侧棱长为
,侧棱长为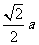 ,若经过对角线
,若经过对角线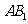 且与对角线
且与对角线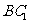 平行的平面交上底面于
平行的平面交上底面于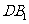 。(1)试确定
。(1)试确定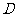 点的位置,并证明你的结论;(2)求平面
点的位置,并证明你的结论;(2)求平面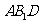 与侧面
与侧面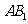 所成的角及平面
所成的角及平面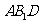 与底面所成的角;(3)求
与底面所成的角;(3)求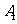 到平面
到平面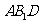 的距离。
的距离。
解:(1)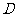 为
为 的中点。连结
的中点。连结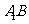 与
与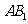 交于
交于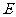 ,则
,则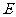 为
为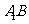 的中点,
的中点,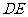 为平面
为平面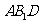
与平面 的交线,∵
的交线,∵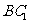 //平面
//平面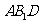
∴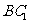 //
//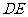 ,∴
,∴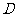 为
为 的中点。
的中点。
(2)过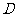 作
作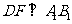 于
于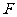 ,由正三棱锥的性质,
,由正三棱锥的性质,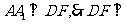 平面
平面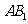 ,连结
,连结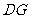 ,则
,则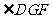 为平面
为平面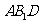 与侧面
与侧面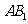 所成的角的平面角,可求得
所成的角的平面角,可求得 ,
,
由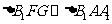 ,得
,得 ,∴
,∴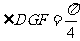
∵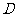 为
为 的中点,∴
的中点,∴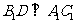 ,由正三棱锥的性质,
,由正三棱锥的性质,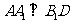 ,∴
,∴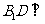 平面
平面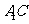
∴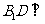
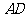 ,∴
,∴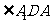 是平面
是平面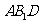 与上底面所成的角的平面角,可求得
与上底面所成的角的平面角,可求得
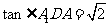 ,∴
,∴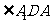
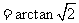
(3)过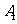 作
作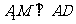 ,∵
,∵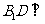 平面
平面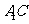 ,∴
,∴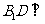
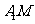 ,∴
,∴ 平面
平面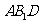
即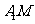 是
是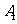 到平面
到平面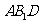 的距离,
的距离,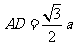 ,∴
,∴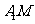
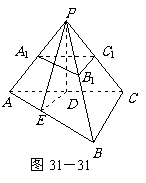
 例3.如图,已知三棱锥
例3.如图,已知三棱锥 的侧面
的侧面 是底角为
是底角为 的等腰三角形,
的等腰三角形, ,且该侧面垂直于底面,
,且该侧面垂直于底面, ,
, ,
, ,
,
(1)求证:二面角 是直二面角;
是直二面角;
(2)求二面角 的正切值;
的正切值;
 (3)若该三棱锥被平行于底面的平面所截,得到一个几何体
(3)若该三棱锥被平行于底面的平面所截,得到一个几何体 ,求几何体
,求几何体 的侧面积.
的侧面积.
证 (1) 如图,在三棱锥 中,取
中,取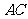 的中点
的中点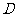 .
.
由题设知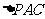 是等腰直角三角形,且
是等腰直角三角形,且 .∴
.∴ 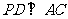 .
.
∵ 平面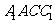
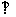 平面
平面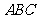 ,∴
,∴ 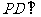 平面
平面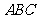 ,
,
∵  ∴
∴ 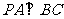 ,∴
,∴ 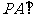 平面
平面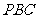 ,
,
∵ 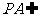 平面
平面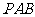 , ∴平面
, ∴平面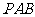
 平面
平面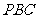 ,
,
即二面角 是直二面角.
是直二面角.
解 (2)作 ,
,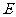 为垂足,则
为垂足,则
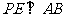 .∴
.∴ 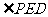 是二面角
是二面角 的平面角.在
的平面角.在 中,
中, ,则
,则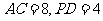
由
 ,得
,得
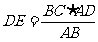 =
= =
= ,
,
∴ 所求正切为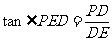 =
=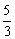 .
.
(3) ∵ 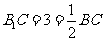 ∴
∴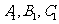 分别是
分别是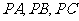 的中点.
的中点.
∴  ,
, 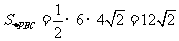 .
.
∵ 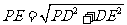 =
=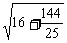 =
=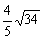 ,
,

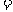
 .
.
∴ 
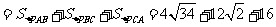 ,∴ 几何体
,∴ 几何体 的侧面积
的侧面积 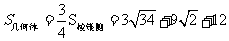
4、若一个三棱锥中,有一条棱长为a,其余棱长均为1,则其体积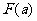 取得最大值时
取得最大值时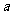 的值为(
)
的值为(
)
A、1
B、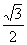 C、
C、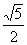 D、
D、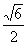
2.如果三棱锥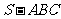 的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点
的底面是不等边三角形,侧面与底面所成的二面角都相等,且顶点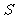 在底面的射影
在底面的射影 在
在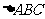 内,那么
内,那么 是
是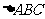 的(
的( 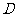 )
)
 垂心
垂心
 重心
重心
 外心
外心  内心
内心
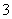 .已知三棱锥
.已知三棱锥 的三个侧面与底面全等,且
的三个侧面与底面全等,且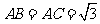 ,
,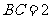 ,则以
,则以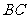 为棱,以面
为棱,以面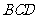 与面
与面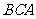 为面的二面角的大小是(
为面的二面角的大小是( 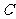 )
)
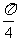
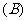
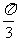
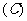
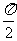
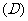
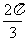
1.给出下列命题:
①底面是正多边形的棱锥是正棱锥;
②侧棱都相等的棱锥是正棱锥;
③侧棱和底面成等角的棱锥是正棱锥;
④侧面和底面所成二面角都相等的棱锥是正棱锥,其中正确命题的个数是(  )
)
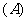

棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形.
[注]:①一个棱锥可以四各面都为直角三角形.
②一个棱柱可以分成等体积的三个三棱锥;所以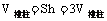 .
.
⑴①正棱锥定义:底面是正多边形;顶点在底面的射影为底面的中心.
[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)
ii. 正四面体是各棱相等,而正三棱锥是底面为正△侧棱与底棱不一定相等
iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形.
②正棱锥的侧面积: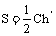 (底面周长为
(底面周长为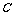 ,斜高为
,斜高为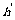 )
)
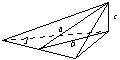 ③棱锥的侧面积与底面积的射影公式:
③棱锥的侧面积与底面积的射影公式: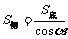 (侧面与底面成的二面角为
(侧面与底面成的二面角为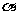 )
)
附: 以知 ⊥
⊥ ,
,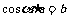 ,
,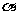 为二面角
为二面角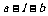 .
.
则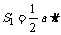 ①,
①,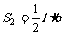 ②,
②, ③
③  ①②③得
①②③得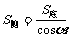 .
.
注:S为任意多边形的面积(可分别多个三角形的方法).
⑵棱锥具有的性质:
①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).
②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.
⑶特殊棱锥的顶点在底面的射影位置:
①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心.
②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心.
③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面多边形内心.
④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.
⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.
⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.
⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;
⑧每个四面体都有内切球,球心 是四面体各个二面角的平分面的交点,到各面的距离等于半径.
是四面体各个二面角的平分面的交点,到各面的距离等于半径.
 [注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)
[注]:i. 各个侧面都是等腰三角形,且底面是正方形的棱锥是正四棱锥.(×)(各个侧面的等腰三角形不知是否全等)
ii. 若一个三角锥,两条对角线互相垂直,则第三对角线必然垂直.
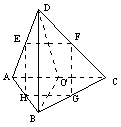 简证:AB⊥CD,AC⊥BD
简证:AB⊥CD,AC⊥BD BC⊥AD. 令
BC⊥AD. 令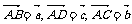
得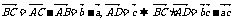 ,已知
,已知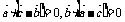
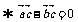 则
则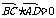 .
.
iii. 空间四边形OABC且四边长相等,则顺次连结各边的中点的四边形一定是矩形.
iv. 若是四边长与对角线分别相等,则顺次连结各边的中点的四边是一定是正方形.
简证:取AC中点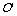 ,则
,则 平面
平面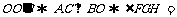 90°易知EFGH为平行四边形
90°易知EFGH为平行四边形 EFGH为长方形.若对角线等,则
EFGH为长方形.若对角线等,则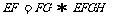 为正方形.
为正方形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com