
1. 若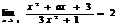 ,则a等于( D )A.1 B.2 C.3 D.4
,则a等于( D )A.1 B.2 C.3 D.4
22.解 (1)f2(x)= 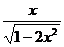 ,f3(x)=
,f3(x)=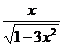
(2)fn(x)=
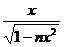
21.[解] (1)∵an=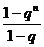
∴An=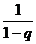 [Cn1(1-q)+Cn2(1-q2)+…+Cnn(1-qn)]
[Cn1(1-q)+Cn2(1-q2)+…+Cnn(1-qn)]
=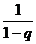 [ Cn1+ Cn2+…+ Cnn-( Cn1q+
Cn2q+…+ Cn1qn)]
[ Cn1+ Cn2+…+ Cnn-( Cn1q+
Cn2q+…+ Cn1qn)]
=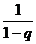 [(2n-1)-(1+q)n+1]=
[(2n-1)-(1+q)n+1]= 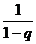 [2n-(1+q)n]
[2n-(1+q)n]
(2)
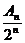 =
=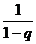 [1-
[1- (
(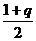 )n]
)n]
∵-3<q<1,∴|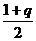 |<1
|<1
∴
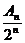 =
=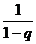
20.解(1)(理)依题意:此试验为独立重复试验问题,所以随机变量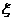 、
、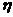 符合二项分布.
符合二项分布.
由二项分布的期望公式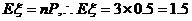
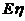 =2×0.5=1.
=2×0.5=1.
(注:也可列分布列根据定义求之)
(2)甲获胜情况有三种:
①甲正面向上1次,乙正面向上0次: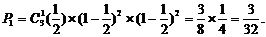
②甲正面向上2次,乙正面向上0次或1次:
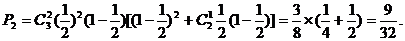
③甲正面向上3次,乙正面向上0次、1次或2次,
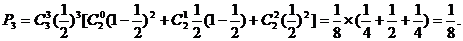
综上所述,甲获胜的概率为: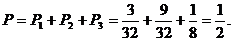
22..设fn(x)=f{[f…f(x)]…}(n个f),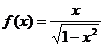 (1)求f2(x),f3(x);(2)猜想fn(x),并证明你的结论。
(1)求f2(x),f3(x);(2)猜想fn(x),并证明你的结论。
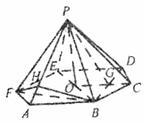 19.(1)证明:连FC,交BD于G,取FC中点O,连PO.
19.(1)证明:连FC,交BD于G,取FC中点O,连PO.
∵正六棱锥P-ABCDEF,∴PO为棱锥的高,FC⊥BD,
∴PO⊥BD,∴BD⊥平面PFC,∴PF⊥BD.
(2)解:∵ABCDEF为正六边形,且AB=2,
∴FO=2,FG=3,OG=1,
连PG,在直角三角形PFO中,PF=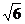 ,FO=2,
,FO=2,
∴PO=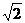 .在直角三角形PGO中,PO=
.在直角三角形PGO中,PO=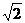 ,OG=1,∴PG=
,OG=1,∴PG=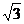
在三角形PGF中,PF=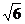 ,FG=3,PG=
,FG=3,PG=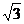 ;
;
∴FG2=PG2+PF2,∴△PFG为直角三角形,
∴PF⊥PG,又PF⊥BD,∴PF⊥平面PBD.
(3)过点F作FH⊥PA于H,连结BH,BF.
∴△PFA≌△PBA,∴BH⊥PA,∴∠FHB为二面角F-PA-B的平面角.
取FA中点S,在△PSF中,PF=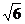 ,FS=1,∴PS=
,FS=1,∴PS=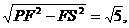
∵在△PFA中,∵FH=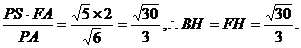
在△BFH中,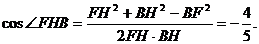
∴二面角F-PA-B的余弦值为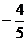 .
.
21.设an=1+q+q2+…+qn-1(n∈N,q≠±1),An=Cn1a1+Cn2a2+…+Cnnan
(1)求An(用n和q表示) (2)当-3<q<1,且q≠-1时,求
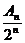 。
。
20.甲、乙两人投掷硬币.甲将一枚硬币投掷3次、记正面朝上的次数为ζ;乙将一枚硬币投掷2次,记正面向上的次数为η.(1)分别求出随机变量ζ和η的数学期望;(2)若规定ζ>η时甲获胜,求甲获胜的概率.
19.
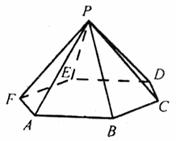 在正六棱锥P-ABCDEF中,AB=2,PF=
在正六棱锥P-ABCDEF中,AB=2,PF=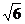 .
.
求证:(1)PF⊥BD;(2)PF⊥平面PBD;
(3)求二面角F-PA-B的余弦值.
18.四面体ABCD中,有以下命题:①若AC⊥BD,AB⊥CD,则AD⊥BC;②若E、F、G分别是BC,AB,CD的中点,则∠EFG的大小等于异面直线AC与BD所成角的大小;③若点O是四面体ABCD外接球的球心,则O在面ABD上的射影是△ABD的外心;④若四个面是全等的三角形,则ABCD为正四面体.其中正确命题序号是___.①、③
17.已知(x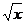 -
-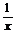 )6展开式的第5项等于
)6展开式的第5项等于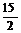 ,那么
,那么 (x-1+x-2+…+x-n)=
。1
(x-1+x-2+…+x-n)=
。1
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com