
4.前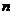 项和的求法:⑴分组求和法;⑵错位相减法;⑶裂项法。
项和的求法:⑴分组求和法;⑵错位相减法;⑶裂项法。
3.常见数列通项的求法:
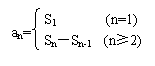 ⑴定义法(利用AP,GP的定义);⑵累加法(
⑴定义法(利用AP,GP的定义);⑵累加法(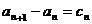 型);⑶公式法:
型);⑶公式法:
⑷累乘法(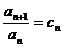 型);⑸待定系数法(
型);⑸待定系数法(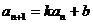 型)转化为
型)转化为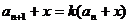
(6)间接法(例如: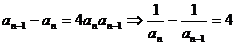 );(7)(理科)数学归纳法。
);(7)(理科)数学归纳法。
2.等差、等比数列性质:




 等差数列
等比数列
等差数列
等比数列

 通项公式
通项公式 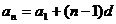
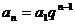
 前n项和
前n项和 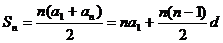
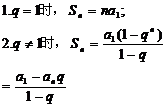
性质 ①an=am+ (n-m)d, ①an=amqn-m;
 ②m+n=p+q时am+an=ap+aq
②m+n=p+q时aman=apaq
②m+n=p+q时am+an=ap+aq
②m+n=p+q时aman=apaq
 ③
③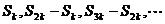 成AP
③
成AP
③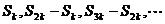 成GP
成GP

 ④
④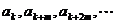 成AP,
成AP,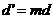 ④
④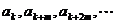 成GP,
成GP,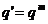
1.定义:
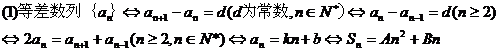
⑵等比数列 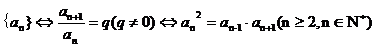
5.三点共线的充要条件:P,A,B三点共线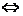
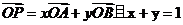 。
。
4.cos<a,b>=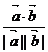 ;
;
3.a·b=|a||b|cos<a,b>= x
x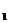 x2+y1y2;
x2+y1y2;
注:①|a|cos<a,b>叫做a在b方向上的投影;|b|cos<a,b>叫做b在a方向上的投影;
②a·b的几何意义:a·b等于|a|与|b|在a方向上的投影|b|cos<a,b>的乘积。
2.向量的平行与垂直: 设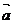 =
=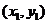 ,
,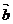 =
=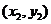 ,且
,且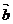
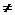
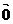 ,则:
,则:
①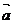 ∥
∥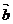
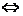
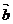 =λ
=λ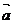
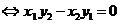 ;
;
②
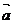
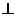
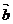 (
(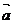
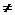
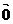 )
)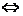
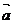 ·
·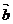 =0
=0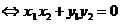 .
.
1.平面上两点间的距离公式: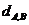
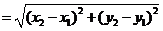 ,其中A
,其中A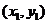 ,B
,B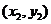 .
.
4.求轨迹的常用方法:(1)定义法:利用圆锥曲线的定义; (2)直接法(列等式);(3)代入法(又称相关点法或坐标转移法);⑷待定系数法;(5)消参法;(6)交轨法;(7)几何法。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com