
5.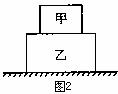 如图2所示,甲、乙两物块叠在一起放在光滑的水平面上处于静止状态,如果乙物体突然受到撞击,甲和乙一起沿平面运动,则下列说法中正确的是( )
如图2所示,甲、乙两物块叠在一起放在光滑的水平面上处于静止状态,如果乙物体突然受到撞击,甲和乙一起沿平面运动,则下列说法中正确的是( )
A.甲与乙的接触面也是光滑的
B.在运动过程中甲和乙之间总存在摩擦力
C.撞击瞬间甲和乙之间有摩擦力,此后甲和乙之间没有摩擦力
D.它们的运动会越来越快
4.一个实心球是由密度分别为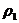 和
和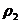 的两个半球组成的(
的两个半球组成的(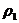 ≠
≠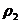 ),测得该球的平均密度恰好和水的密度相等,则 ( )
),测得该球的平均密度恰好和水的密度相等,则 ( )
A.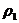 +
+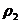 =
=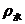 B. |
B. |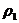 -
-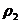 |=
|=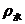
C.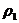 +
+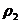 =2
=2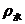 D.
D.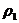 +
+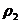 =4
=4
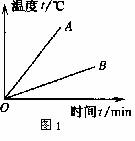
3.在相同条件下,对质量为m1、比热为c1的物质A和质量为m2、比热为c2的物质B均匀加热(物质A、B的温度随加热时间的变化情况如图1所示),根据图像可以推断一定不正确的结论是( )
A.若c1 = c2,则m1 < m2 B.若c1 > c2,则m1 > m2
C.若m1 = m2,则c1 < c2 D.若m1 < m2,则c1 > c2
2.某同学使用天平时,游码固定在4克处,将天平调平衡。在测量物体质量时,右盘加上18克砝码,再把游码移到零刻线处,天平横梁再次平衡。则所称物体质量为 ( )
 A.10克 B.22克 C.14克 D.26克
A.10克 B.22克 C.14克 D.26克
1.地球不停地自西向东自转,跳远运动员想利用这个自然现象跳得更远些,下列结论中正确的是:( )
A.由西向东跳有利 B.由东向西跳有利
C.由南向北跳有利 D.无论何方,效果相同
转借课本事例,就是指在选材时将已学过的语文课本中有关篇目章节内容、相关故事、典故以及经典例子组合转借到议论文里,让文章展示出深厚的文化底蕴。运用这种方法时,要注意两点:一是借用课本中的事例等素材,应该注意紧扣论点,精心选择能够突出中心的材料,并且做到材料典型充实,论证层次清晰,语言简洁;二是转借课本材料时要尽量灵活运用,最好不要只是引用事例,可化用诗句作标题,可演绎典故来分析,可引用名句作论据,这样才能体现考生所积累的文化底蕴。如,广东一考生在一篇题为《此时有声胜无声》的满分作文中,就“语言与沟通”这一话题,采用了经典组合策略,分别激活并使用“烛之武竟能用一段话使秦师从边境中退去,挽救一国家,一个即将灭亡的国家”(《烛之武退秦师》)、“曹植以惊人的智慧吟出了‘煮豆燃豆,豆在釜中泣。本是同根生,相煎何太急?’的七步诗,从而使曹丕给曹植留下了一条命”(《曹植七步赋诗》)“触龙竟能用语言的沟通来说服赵太后送自己最心安的儿子长安君去当人质”(《触龙说赵太后》)等课文中的经典事例,用来阐述语言沟通、说话艺术在拯救国家危难上和在挽救个人危难时展示的力量。全文纵横开阖且丰富多彩,既撷华掇英,展示文化底蕴,又增强论证的力量和说理的感染力,足显作者灵活自如地组合课文中的经典事例对“语言与沟通”问题深刻的认识。
当然,在议论文写作中筛选提炼材料的方法还有很多,如,可以赋予典故新意,可以挖掘小事深意,可以汇聚文史人物,可以演绎诗词名句,只要善于积累,巧于提炼,就不愁没有可写之材。
在作文中选用某一个生活现象作素材,并从这一生活现象中得出某一生活启示,以此来引出文章的观点,突显文章的主旨。用作迁移的生活现象用在文章的开头,可以引出观点;用在文章的中间,可以充当论据。具体运用时,可以作相同方向迁移,即把一种生活现象中获得的感悟或思考,迁移到与之类似的另一种生活现象,以解决问题,这种迁移主要借助时、空变换来进行;也可以作相反方向迁移,即把某种生活现象中获得的思考用于也与之相反、相对的生活现象,这种迁移主要借助事物的对立统一关系进行。如,有一篇题为《拔丝苹果的启示》的议论文是这样来迁移生活现象的:“东北有一道名菜,叫拔丝苹果。就是将切好的一块块苹果肉放在滚烫的糖浆里一过,捞出来金黄金黄的、热腾腾的一大盘。趁热用筷子夹起一块,那还没冷却的糖浆就被拔成一丝一丝的,站得老高还不能把它们完全拔断。这时配菜一起出的一碗凉开水起作用了,你把苹果肉放在水里一蘸,糖浆丝遇冷而变脆了,放到嘴里,外面是甜而清脆,里面则是热而柔嫩,真绝了。吃完之后不禁想到,在生活中,热烈的事物有时候不也需要降降温吗?”“面对生活,我们首先要以火一般的热情去追求成功,在达到目标之后则应以冰一样的冷静去分析总结,在思索中找寻人生新的亮点,走到另一个跋涉的起点。”这里,作者从吃名菜“拔丝苹果”这一生活现象写起,自然而然地引出论点,如同朋友娓娓谈心,毫无居高临下盛气凌人的教训意味,给人以亲切之感。
聚合新闻热点,就是指选用新闻时事热点材料来表达主题。这种用材方法,既能使文章的内容富有时代气息,也能彰显出考生对社会生活、对国际国内新闻极强的敏感性,常常受到阅卷老师的好评。如,每年就有不少考生在议论文中选用了感动中国十大新闻人物事例以及新近发生的新闻热点材料,从而使文章因洋溢着鲜明的时代色彩而获得满分。但用好这一方法,也要注意两点:一是平时要注意随时留心周围发生的事情,注意社会上新近发生的重大事件,注意各种媒体中的新闻热点与焦点;二是新闻热点素材可以在文章的开头运用,以引出观点,也可以在文章的主体部分运用,以论证观点。如,2008年高考广东一考生在写《不要轻易说“不”》这篇命题作文时,先通过马云的事例着力论述“不要不加以认真思索,就轻易说‘不’”的观点,然后递进一层提出了“对于一些事情,我们却要不假思索地说‘不’”的观点,并选取汶川地震、达赖搞藏独、DNN侮辱中国人民、莎朗·斯通提出“地震报应”论等新近发生的新闻热点材料作论据加以论证,从而得出“让我们理性对待‘不’字”的结论。又如一考生在论述“诚信,正离去,代之以欺诈与虚伪”这一观点时,列举了“各种假冒伪劣商品屡禁不止;外地民工辛苦一年非但得不到血汗钱反被包工头毒打一顿;恒源祥举行试穿活动,送出去的500件衣服回收却不到10%;广东普宁码头边一间间简陋的棚子里,人们用特制的带铁钉的刷子大肆生产‘垃圾衣’”等新闻热点材料,从而让读者感受到“需要来一次心灵的净化”的必要性。
9.(2008年四川省成都市一诊)已知函数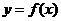 是定义域为R的偶函数,其图像均在x轴
是定义域为R的偶函数,其图像均在x轴
的上方,对任意的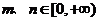 ,都有
,都有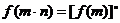 ,且
,且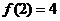 ,又当
,又当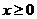 时,其导函数
时,其导函数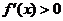 恒成立。
恒成立。
(Ⅰ)求f(0)、f(-1)的值;
(Ⅱ)解关于x的不等式: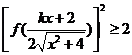 ,其中
,其中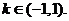
解 (1)由f(m·n)=[f(m)]n得:f(0)=f(0×0)=[f(0)]0
∵函数f(x)的图象均在x轴的上方,∴f(0)>0,∴f(0)=1 ……………………………3分
∵f(2)=f(1×2)=[f(1)]2=4,又f(x)>0∴f(1)=2,f(-1)=f(1)=2 …………………3分
(2)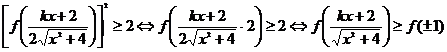
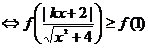
又当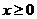 时,其导函数
时,其导函数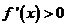 恒成立,∴
恒成立,∴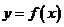 在区间
在区间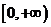 上为单调递增函数
上为单调递增函数
∴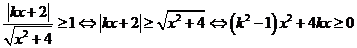
①当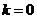 时,
时,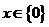 ;
;
②当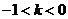 时,
时,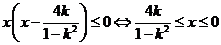 ,∴
,∴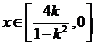 ;
;
③当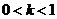 时,
时,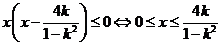 ,∴
,∴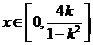
综上所述:当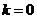 时,
时,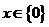 ;当
;当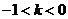 时,
时,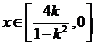 ;
;
当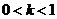 时,
时,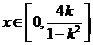 。
。
8.(2007年江苏省淮安市)已知函数F(x)=|2x-t|-x3+x+1(x∈R,t为常数,t∈R)
(1)写出此函数F(x)在R上的单调区间;
(2)若方程F(x)-m=0恰有两解,求实数m的值。
解 (1)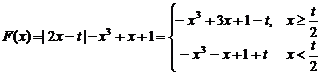 ∴
∴
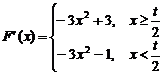
由-3x2+3=0 得x1=-1,x2=1,而-3x2-1<0恒成立
∴ i) 当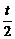 <-1时,F(x)在区间(-∞,-1)上是减函数
<-1时,F(x)在区间(-∞,-1)上是减函数
在区间(-1,1)上是增函数,在区间(1,+∞)上是减函数
ii) 当1>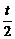 ≥-1时,F(x)在区间(-∞,
≥-1时,F(x)在区间(-∞,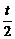 )上是减函数
)上是减函数
在区间(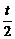 ,1)上是增函数,在区间(1,+∞)上是减函数
,1)上是增函数,在区间(1,+∞)上是减函数
iii) 当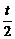 ≥1时,F(x)在(-∞,+∞)上是减函数
≥1时,F(x)在(-∞,+∞)上是减函数
(2)由(1)可知
i) 当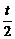 <-1时,F(x)在x=-1处取得极小值-1-t,
<-1时,F(x)在x=-1处取得极小值-1-t,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=-1-t或m=3-t
ii) 当-1≤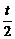 <1,F(x)在x=
<1,F(x)在x=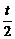 处取值为
处取值为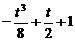 ,
,
在x=1处取得极大值3-t,若方程F(x)-m=0恰有两解,
此时m=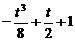 或m=3-t
或m=3-t
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com