
4.(2008海南理11)已知点P在抛物线y2 = 4x上,那么点P到点Q(2,-1)的距离与
点P 到抛物线焦点距离之和取得最小值时,点P的坐标为 ( )
A.(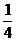 ,-1) B.(
,-1) B.(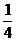 ,1)
C.(1,2) D.(1,-2)
,1)
C.(1,2) D.(1,-2)
答案 A
3.(2008全国Ⅱ理9)设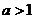 ,则双曲线
,则双曲线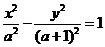 的离心率
的离心率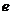 的取值范围是
( )
的取值范围是
( )
A.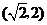 B.
B.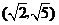 C.
C.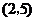 D.
D.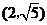
答案 B
2.(2008江西理7)已知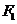 、
、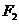 是椭圆的两个焦点,满足
是椭圆的两个焦点,满足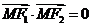 的点
的点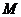 总在椭圆内部,则椭圆离心率的取值范围是 ( )
总在椭圆内部,则椭圆离心率的取值范围是 ( )
A.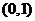 B.
B.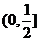 C.
C.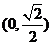 D.
D.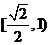
答案 C
1.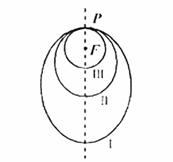 (2008湖北卷10)如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞
(2008湖北卷10)如图所示,“嫦娥一号”探月卫星沿地月转移轨道飞
向月球,在月球附近一点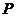 轨进入以月球球心
轨进入以月球球心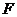 为一个焦点的椭圆
为一个焦点的椭圆
轨道Ⅰ绕月飞行,之后卫星在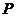 变点第二次变轨进入仍以月球球心
变点第二次变轨进入仍以月球球心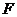 为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在
为一个焦点的椭圆轨道Ⅱ绕月飞行,最终卫星在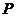 点第三次变轨进入以
点第三次变轨进入以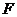 为圆心的圆形轨道Ⅲ绕月飞行,若用
为圆心的圆形轨道Ⅲ绕月飞行,若用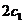 和
和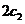 分别表示椭轨道Ⅰ和Ⅱ的焦距,用
分别表示椭轨道Ⅰ和Ⅱ的焦距,用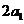 和
和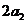 分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长,给出下列式子:
①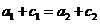 ; ②
; ②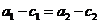 ; ③
; ③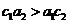 ;
④
;
④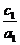 <
<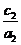 .
.
其中正确式子的序号是 ( )
A. ①③ B. ②③ C. ①④ D. ②④
答案 B
72.(2009重庆卷文)(本小题满分12分)
已知以原点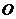 为中心的双曲线的一条准线方程为
为中心的双曲线的一条准线方程为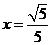 ,离心率
,离心率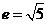 .
.
(Ⅰ)求该双曲线的方程;
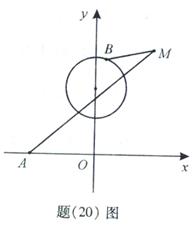
(Ⅱ)如题(20)图,点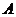 的坐标为
的坐标为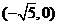 ,
,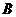 是圆
是圆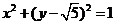 上的点,点
上的点,点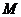 在双曲线右支上,求
在双曲线右支上,求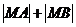 的最小值,并求此时
的最小值,并求此时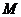 点的坐标;
点的坐标; 



解 (Ⅰ)由题意可知,双曲线的焦点在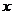 轴上,故可设双曲线的方程为
轴上,故可设双曲线的方程为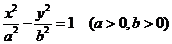 ,设
,设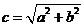 ,由准线方程为
,由准线方程为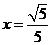 得
得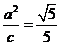 ,由
,由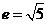 得
得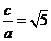 解得
解得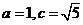 从而
从而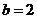 ,
,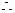 该双曲线的方程为
该双曲线的方程为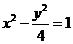 .
.
(Ⅱ)设点D的坐标为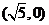 ,则点A、D为双曲线的焦点,
,则点A、D为双曲线的焦点,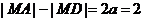
所以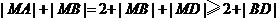 ,
,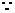
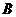 是圆
是圆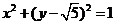 上的点,其圆心为
上的点,其圆心为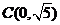 ,半径为1,故
,半径为1,故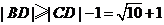
从而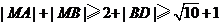
当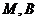 在线段CD上时取等号,此时
在线段CD上时取等号,此时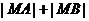 的最小值为
的最小值为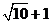
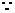 直线CD的方程为
直线CD的方程为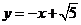 ,因点M在双曲线右支上,故
,因点M在双曲线右支上,故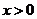
由方程组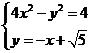 解得
解得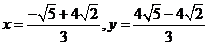
所以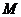 点的坐标为
点的坐标为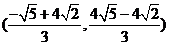 .
. 



2005-2008年高考题
71.(2009重庆卷理)(本小题满分12分)
已知以原点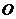 为中心的椭圆的一条准线方程为
为中心的椭圆的一条准线方程为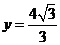 ,离心率
,离心率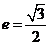 ,
,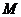 是椭圆上的动点.
是椭圆上的动点.
(Ⅰ)若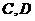 的坐标分别是
的坐标分别是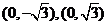 ,求
,求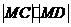 的最大值;
的最大值;
(Ⅱ)如题图,点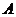 的坐标为
的坐标为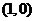 ,
,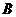 是圆
是圆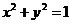 上的点,
上的点,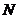 是点
是点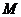 在
在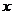 轴上的射影,点
轴上的射影,点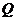 满足条件:
满足条件: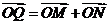 ,
,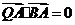 .求线段
.求线段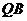 的中点
的中点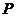 的轨迹方程;
的轨迹方程;
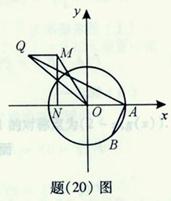


解 (Ⅰ)由题设条件知焦点在y轴上,故设椭圆方程为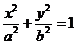 (a >b> 0 ).
(a >b> 0 ).
设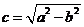 ,由准线方程
,由准线方程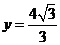 得.由
得.由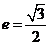 得
得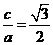 ,解得
a = 2 ,c =
,解得
a = 2 ,c = 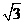 ,从而
b = 1,椭圆方程为
,从而
b = 1,椭圆方程为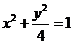 .
.
又易知C,D两点是椭圆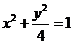 的焦点,所以,
的焦点,所以,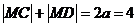
从而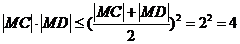 ,当且仅当
,当且仅当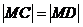 ,
,
即点M的坐标为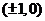 时上式取等号,
时上式取等号,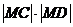 的最大值为4 .
的最大值为4 . 

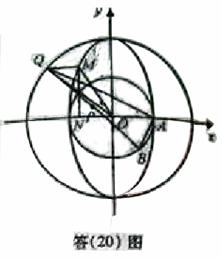
(II)如图(20)图,设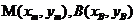
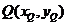 .因为
.因为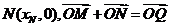 ,故
,故
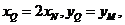
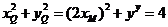 ①
①
因为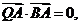
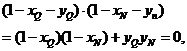
所以 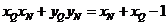 . ②
. ②
记P点的坐标为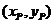 ,因为P是BQ的中点
,因为P是BQ的中点
所以 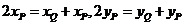
由因为 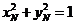 ,结合①,②得
,结合①,②得
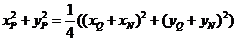


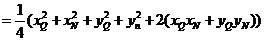
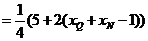
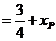
故动点P的估计方程为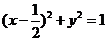
70.(2009上海卷文)(本题满分16分)
已知双曲线C的中心是原点,右焦点为F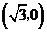 ,一条渐近线m:
,一条渐近线m: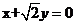 ,设过点A
,设过点A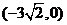 的直线l的方向向量
的直线l的方向向量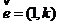 。
。
(1) 求双曲线C的方程;
(2) 若过原点的直线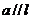 ,且a与l的距离为
,且a与l的距离为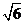 ,求K的值;
,求K的值;
(3) 证明:当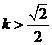 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为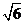 .
.
(1)解 设双曲线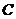 的方程为
的方程为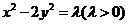
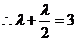 ,解得
,解得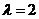 ,双曲线
,双曲线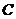 的方程为
的方程为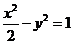
(2)解 直线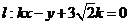 ,直线
,直线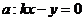
由题意,得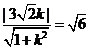 ,解得
,解得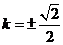
(3)证明 方法一 设过原点且平行于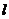 的直线
的直线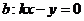
则直线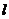 与
与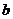 的距离
的距离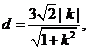 当
当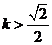 时,
时,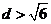


又双曲线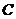 的渐近线为
的渐近线为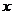
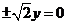


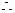 双曲线
双曲线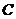 的右支在直线
的右支在直线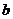 的右下方,
的右下方,
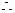 双曲线
双曲线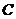 右支上的任意点到直线
右支上的任意点到直线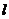 的距离大于
的距离大于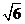 。
。
故在双曲线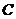 的右支上不存在点
的右支上不存在点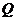 ,使之到直线
,使之到直线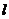 的距离为
的距离为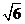
(3)方法二 假设双曲线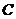 右支上存在点
右支上存在点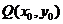 到直线
到直线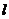 的距离为
的距离为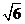 ,
,
则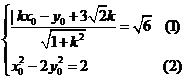
由(1)得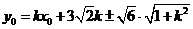
设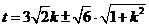 ,
,
当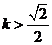 时,
时,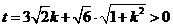 ;
;
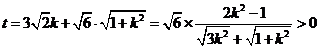
将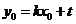 代入(2)得
代入(2)得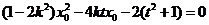
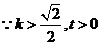 ,
, 

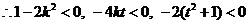
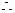 方程
方程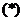 不存在正根,即假设不成立,
不存在正根,即假设不成立,
故在双曲线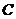 的右支上不存在点
的右支上不存在点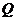 ,使之到直线
,使之到直线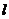 的距离为
的距离为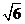


69.(2009年上海卷理)(本题满分16分)
已知双曲线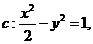 设过点
设过点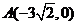 的直线l的方向向量
的直线l的方向向量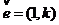


(1) 当直线l与双曲线C的一条渐近线m平行时,求直线l的方程及l与m的距离;
(2)
证明:当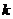 >
>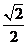 时,在双曲线C的右支上不存在点Q,使之到直线l的距离为
时,在双曲线C的右支上不存在点Q,使之到直线l的距离为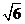 。
。
(1)解 双曲线C的渐近线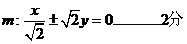
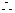 直线l的方程
直线l的方程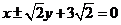
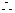 直线l与m的距离
直线l与m的距离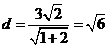

(2)证明 方法一设过原点且平行与l的直线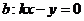
则直线l与b的距离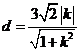
当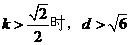


又双曲线C的渐近线为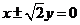

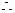 双曲线C的右支在直线b的右下方,
双曲线C的右支在直线b的右下方,
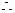 双曲线
双曲线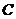 右支上的任意点到直线
右支上的任意点到直线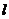 的距离为
的距离为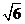 。
。
故在双曲线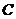 的右支上不存在点
的右支上不存在点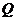 ,使之到直线
,使之到直线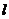 的距离为
的距离为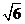 。
。
(2)方法二 双曲线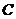 的右支上存在点
的右支上存在点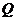
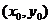 到直线
到直线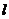 的距离为
的距离为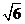 ,
,
则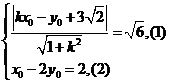
由(1)得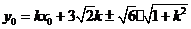 ,
, 
设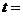
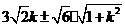



当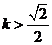 ,
,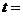
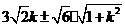
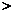 0
0
将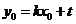 代入(2)得
代入(2)得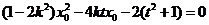 (*)
(*)
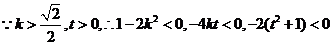
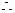 方程(*)不存在正根,即假设不成立
方程(*)不存在正根,即假设不成立


故在双曲线C的右支上不存在Q,使之到直线l 的距离为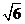
68.(2009福建卷文)(本小题满分14分)
已知直线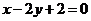 经过椭圆
经过椭圆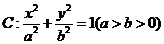

 的左顶点A和上顶点D,椭圆
的左顶点A和上顶点D,椭圆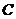 的右顶点为
的右顶点为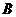 ,点
,点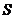 和椭圆
和椭圆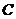 上位于
上位于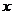 轴上方的动点,直线,
轴上方的动点,直线,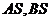 与直线
与直线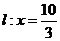
分别交于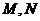 两点。
两点。
(I)求椭圆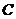 的方程;
的方程;
(Ⅱ)求线段MN的长度的最小值;
(Ⅲ)当线段MN的长度最小时,在椭圆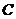 上是否存在这样的点
上是否存在这样的点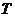 ,使得
,使得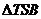 的面积为
的面积为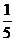 ?若存在,确定点
?若存在,确定点 的个数,若不存在,说明理由
的个数,若不存在,说明理由
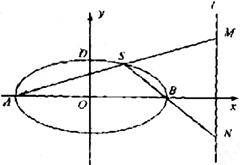
解 方法一(I)由已知得,椭圆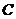 的左顶点为
的左顶点为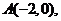 上顶点为
上顶点为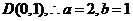
故椭圆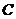 的方程为
的方程为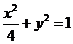
(Ⅱ)直线AS的斜率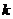 显然存在,且
显然存在,且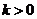 ,故可设直线
,故可设直线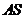 的方程为
的方程为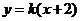 ,
,
从而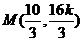
由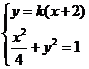 得
得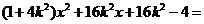 0
0
设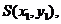 则
则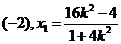 得
得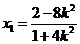 ,从而
,从而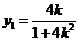


即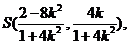 又
又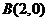
由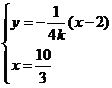 得
得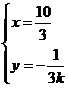
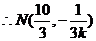
故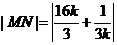
又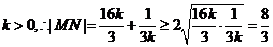

当且仅当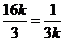 ,即
,即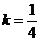 时等号成立
时等号成立 

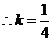 时,线段
时,线段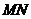 的长度取最小值
的长度取最小值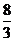
(Ⅲ)由(Ⅱ)可知,当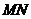 取最小值时,
取最小值时,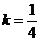
此时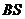 的方程为
的方程为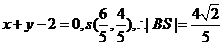
要使椭圆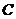 上存在点
上存在点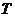 ,使得
,使得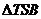 的面积等于
的面积等于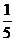 ,只须
,只须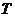 到直线
到直线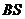 的距离等于
的距离等于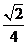 ,所以
,所以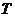 在平行于
在平行于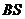 且与
且与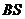 距离等于
距离等于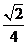 的直线
的直线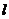 上。
上。
设直线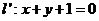
则由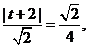 解得
解得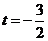 或
或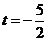


67.(2009湖南卷理)(本小题满分13分)在平面直角坐标系xOy中,点P到点F(3,0)的距离的4倍与它到直线x=2的距离的3倍之和记为d,当P点运动时,d恒等于
点P的横坐标与18之和




(Ⅰ)求点P的轨迹C;
(Ⅱ)设过点F的直线l与轨迹C相交于M,N两点,求线段
MN长度的最大值。
解(Ⅰ)设点P的坐标为(x,y),则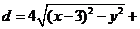 3︳x-2︳
3︳x-2︳
由题设
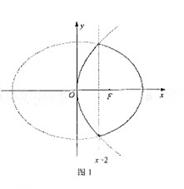 当x>2时,由①得
当x>2时,由①得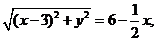 化简得
化简得 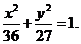


当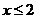 时 由①得
时 由①得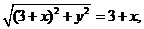 化简得
化简得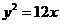
故点P的轨迹C是椭圆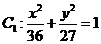 在直线x=2的右侧部分与
在直线x=2的右侧部分与
抛物线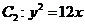 在直线x=2的左侧部分(包括它与直线x=2的交点)
在直线x=2的左侧部分(包括它与直线x=2的交点)
所组成的曲线,参见图1
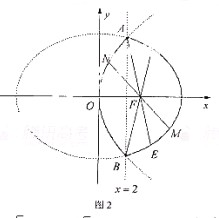 (Ⅱ)如图2所示,易知直线x=2与
(Ⅱ)如图2所示,易知直线x=2与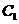 ,
,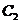 的交点都是
的交点都是
A(2,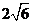 ),B(2,
),B(2,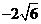 ),
),
直线AF,BF的斜率分别为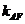 =
=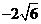 ,
,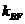 =
=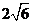 .
.
当点P在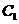 上时,由②知
上时,由②知
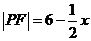 .
④
.
④ 

当点P在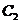 上时,由③知
上时,由③知 

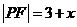 ⑤
⑤
若直线l的斜率k存在,则直线l的方程为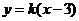
(i)当k≤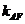 ,或k≥
,或k≥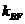 ,即k≤-2
,即k≤-2 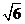 时,直线I与轨迹C的两个交点M(
时,直线I与轨迹C的两个交点M(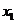 ,
,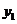 ),N(
),N(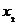 ,
,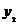 )都在C
)都在C 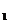 上,此时由④知
上,此时由④知
∣MF∣= 6 - 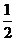
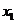 ∣NF∣= 6 -
∣NF∣= 6 - 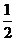
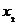


从而∣MN∣= ∣MF∣+ ∣NF∣= (6 - 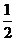
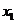 )+ (6 -
)+ (6 - 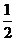
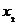 )=12 -
)=12 - 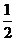 (
(
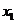 +
+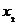 )
)
由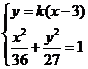 得
得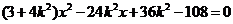 则
则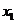 ,
,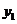 是这个方程的两根,所以
是这个方程的两根,所以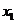 +
+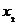 =
=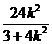 *∣MN∣=12 -
*∣MN∣=12 - 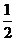 (
(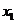 +
+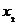 )=12 -
)=12 - 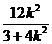
因为当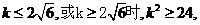
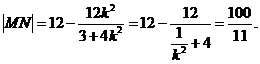


当且仅当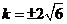 时,等号成立。
时,等号成立。
(2)当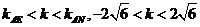 时,直线L与轨迹C的两个交点
时,直线L与轨迹C的两个交点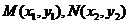 分别在
分别在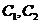 上,不妨设点
上,不妨设点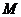 在
在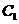 上,点
上,点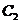 上,则④⑤知,
上,则④⑤知,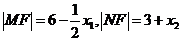
设直线AF与椭圆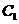 的另一交点为E
的另一交点为E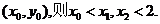
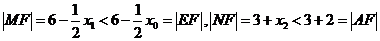
所以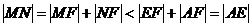 。而点A,E都在
。而点A,E都在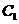 上,且
上,且
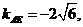 有(1)知
有(1)知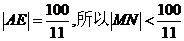


若直线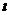 的斜率不存在,则
的斜率不存在,则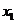 =
=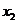 =3,此时
=3,此时
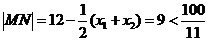
综上所述,线段MN长度的最大值为 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com