
5.(辽宁省大连市第二十四中学2009届高三高考模拟)已知双曲线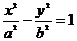 (a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是 ( )
A.(1,2) B.(-1,2) C.(2,+∞) D.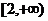
答案 D
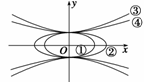
3.(湖北省武汉市第四十九中学2009届高三年级十月月考)图中共顶点
的椭圆①、②与双曲线③、④的离心率分别为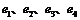 ,
,
其大小关系为 ( )
A.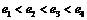 B.
B.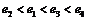
C.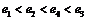 D.
D.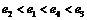
答案 C
2.(广东省佛山市三水中学2009届高三上学期期中考试)若椭圆经过点P(2,3),且焦点为F1(-2,0), F2 (2,0),则这个椭圆的离心率等于 ( )
A. B. C. D.
 答案 C
答案 C
1. (广东省华南师范附属中学2009届高三上学期第三次综合测试)曲线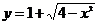
(x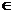 [-2,2])与直线
[-2,2])与直线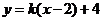 两个公共点时,实效
两个公共点时,实效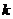 的取值范围是 ( )
的取值范围是 ( )
A.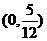 B.
B.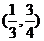 C.
C.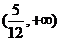 D.
D.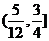
答案 D
21.(2008全国Ⅰ理21)双曲线的中心为原点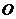 ,焦点在
,焦点在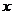 轴上,两条渐近线分别为l1,l2,
轴上,两条渐近线分别为l1,l2,
经过右焦点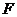 垂直于l1的直线分别交l1、l2于
垂直于l1的直线分别交l1、l2于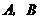 两点.已知
两点.已知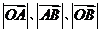 成等差数
成等差数
列,且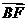 与
与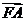 同向.
同向.
(Ⅰ)求双曲线的离心率;
(Ⅱ)设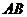 被双曲线所截得的线段的长为4,求双曲线的方程.
被双曲线所截得的线段的长为4,求双曲线的方程.
解:(Ⅰ)设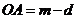 ,
,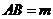 ,
,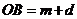
由勾股定理可得: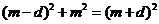
得: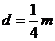 ,
, ,
,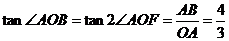
由倍角公式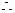
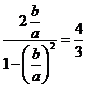 ,解得
,解得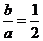 ,则离心率
,则离心率 .
.
(Ⅱ)过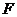 直线方程为
直线方程为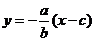 ,与双曲线方程
,与双曲线方程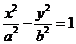 联立
联立
将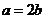 ,
,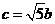 代入,化简有
代入,化简有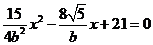
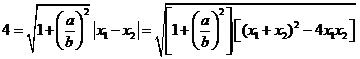
将数值代入,有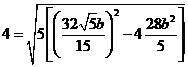 ,解得
,解得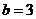
故所求的双曲线方程为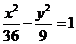 。
。
20.(2005江西理)以下四个关于圆锥曲线的命题中:
①设A、B为两个定点,k为非零常数,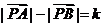 ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②过定圆C上一定点A作圆的动点弦AB,O为坐标原点,若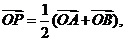 则动点
则动点
P的轨迹为椭圆;
③方程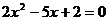 的两根可分别作为椭圆和双曲线的离心率;
的两根可分别作为椭圆和双曲线的离心率;
④双曲线 有相同的焦点.
有相同的焦点.
其中真命题的序号为 (写出所有真命题的序号)
答案 ③④
19.(2006上海理7) 已知椭圆中心在原点,一个焦点为F(-2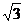 ,0),且长轴长是短轴长
,0),且长轴长是短轴长
的2倍,则该椭圆的标准方程是 .
答案 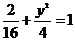
18.(2007上海春季6) 在平面直角坐标系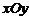 中,若抛物线
中,若抛物线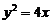 上的点
上的点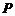 到该抛物线的
到该抛物线的
焦点的距离为6,则点P的横坐标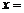 .
.
答案 5
17.(2007山东理)设O是坐标原点,F是抛物线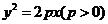 的焦点,A是抛物线上
的焦点,A是抛物线上
的一点,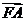 与
与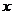 轴正向的夹角为
轴正向的夹角为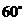 ,则
,则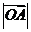 为
.
为
.
答案 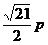
16.(2008上海春季7) 已知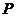 是双曲线
是双曲线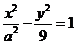 右支上的一点,双曲线的一条渐近线方
右支上的一点,双曲线的一条渐近线方
程为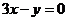 . 设
. 设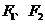 分别为双曲线的左、右焦点. 若
分别为双曲线的左、右焦点. 若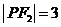 ,则
,则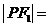 .
.
答案 5
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com