
22.(2009年上海卷理)某学校要从5名男生和2名女生中选出2人作为上海世博会志愿者,若用随机变量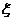 表示选出的志愿者中女生的人数,则数学期望
表示选出的志愿者中女生的人数,则数学期望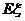 ____________(结果用最简分数表示).
____________(结果用最简分数表示). 

[答案]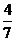
[解析]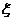 可取0,1,2,因此P(
可取0,1,2,因此P(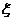 =0)=
=0)=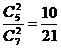 , P(
, P(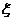 =1)=
=1)=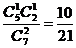 ,
,
P(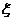 =2)=
=2)=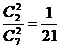 ,
,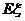 =0×
=0×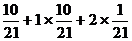 =
=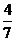
21.(2009浙江卷文)有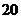 张卡片,每张卡片上分别标有两个连续的自然数
张卡片,每张卡片上分别标有两个连续的自然数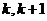 ,其中
,其中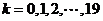 .
.
从这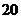 张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取到
张卡片中任取一张,记事件“该卡片上两个数的各位数字之和(例如:若取到
标有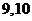 的卡片,则卡片上两个数的各位数字之和为
的卡片,则卡片上两个数的各位数字之和为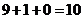 )不小于
)不小于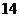 ”为
”为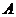 ,
,
则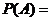 .
. 

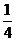 [命题意图]此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
[命题意图]此题是一个排列组合问题,既考查了分析问题,解决问题的能力,更侧重于考查学生便举问题解决实际困难的能力和水平
[解析]对于大于14的点数的情况通过列举可得有5种情况,即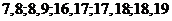 ,而基本事件有20种,因此
,而基本事件有20种,因此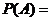
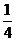


20.(2009浙江卷理)甲、乙、丙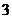 人站到共有
人站到共有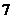 级的台阶上,若每级台阶最多站
级的台阶上,若每级台阶最多站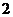 人,同一级台阶上的人不区分站的位置,则不同的站法种数是
(用数字作答).
人,同一级台阶上的人不区分站的位置,则不同的站法种数是
(用数字作答).
答案:336
[解析]对于7个台阶上每一个只站一人,则有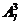 种;若有一个台阶有2人,另一个是1人,则共有
种;若有一个台阶有2人,另一个是1人,则共有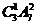 种,因此共有不同的站法种数是336种.
种,因此共有不同的站法种数是336种. 

19.(2009天津卷理)用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 个(用数字作答)
[考点定位]本小题考查排列实际问题,基础题。
解析:个位、十位和百位上的数字为3个偶数的有: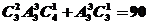 种;个位、十位和百位上的数字为1个偶数2个奇数的有:
种;个位、十位和百位上的数字为1个偶数2个奇数的有: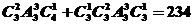 种,所以共有
种,所以共有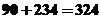 个。
个。
18.(2009宁夏海南卷理)7名志愿者中安排6人在周六、周日两天参加社区公益活动。若每天安排3人,则不同的安排方案共有________________种(用数字作答)。
解析: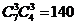 ,
,
答案:140
17.(2009重庆卷文)12个篮球队中有3个强队,将这12个队任意分成3个组(每组4个队),则3个强队恰好被分在同一组的概率为( )
A.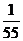 B.
B.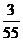 C.
C.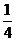 D.
D.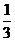
[答案]B
解析因为将12个组分成4个组的分法有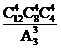 种,而3个强队恰好被分在同一组分法有
种,而3个强队恰好被分在同一组分法有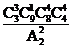 ,故个强队恰好被分在同一组的概率为
,故个强队恰好被分在同一组的概率为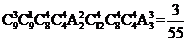 。
。
16.(2009四川卷理)3位男生和3位女生共6位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是
A. 360 B. 188 C. 216 D. 96
[考点定位]本小题考查排列综合问题,基础题。
解析:6位同学站成一排,3位女生中有且只有两位女生相邻的排法有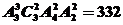 种,其中男生甲站两端的有
种,其中男生甲站两端的有 ,符合条件的排法故共有188
,符合条件的排法故共有188
解析2:由题意有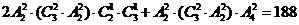 ,选B。
,选B。
14.(2009陕西卷文)从1,2,3,4,5,6,7这七个数字中任取两个奇数和两个偶数,组成没有重复数字的四位数,其中奇数的个数为
(A)432 (B)288 (C) 216 (D)108网
答案:C.
解析:首先个位数字必须为奇数,从1,3,5,7四个中选择一个有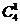 种,再丛剩余3个奇数中选择一个,从2,4,6三个偶数中选择两个,进行十位,百位,千位三个位置的全排。则共有
种,再丛剩余3个奇数中选择一个,从2,4,6三个偶数中选择两个,进行十位,百位,千位三个位置的全排。则共有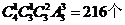 故选C.
故选C. 

 15.(2009湖南卷理)从10名大学生毕业生中选3个人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数位
15.(2009湖南卷理)从10名大学生毕业生中选3个人担任村长助理,则甲、乙至少有1人入选,而丙没有入选的不同选法的种数位 
 [
C]
[
C] 

A 85 B 56 C 49 D 28
[答案]:C
[解析]解析由条件可分为两类:一类是甲乙两人只去一个的选法有: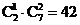 ,另一类是甲乙都去的选法有
,另一类是甲乙都去的选法有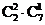 =7,所以共有42+7=49,即选C项。
=7,所以共有42+7=49,即选C项。
13.(2009四川卷文)2位男生和3位女生共5位同学站成一排,若男生甲不站两端,3位女生中有且只有两位女生相邻,则不同排法的种数是
A. 60 B. 48 C. 42 D. 36
[答案]B
[解析]解法一、从3名女生中任取2人“捆”在一起记作A,(A共有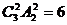 种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;则男生甲必须在A、B之间(若甲在A、B两端。则为使A、B不相邻,只有把男生乙排在A、B之间,此时就不能满足男生甲不在两端的要求)此时共有6×2=12种排法(A左B右和A右B左)最后再在排好的三个元素中选出四个位置插入乙,所以,共有12×4=48种不同排法。
种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;则男生甲必须在A、B之间(若甲在A、B两端。则为使A、B不相邻,只有把男生乙排在A、B之间,此时就不能满足男生甲不在两端的要求)此时共有6×2=12种排法(A左B右和A右B左)最后再在排好的三个元素中选出四个位置插入乙,所以,共有12×4=48种不同排法。
解法二;同解法一,从3名女生中任取2人“捆”在一起记作A,(A共有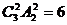 种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;为使男生甲不在两端可分三类情况:
种不同排法),剩下一名女生记作B,两名男生分别记作甲、乙;为使男生甲不在两端可分三类情况:
第一类:女生A、B在两端,男生甲、乙在中间,共有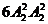 =24种排法;
=24种排法;
第二类:“捆绑”A和男生乙在两端,则中间女生B和男生甲只有一种排法,此时共有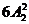 =12种排法
=12种排法
第三类:女生B和男生乙在两端,同样中间“捆绑”A和男生甲也只有一种排法。
此时共有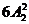 =12种排法
=12种排法
三类之和为24+12+12=48种。
12.(2009全国卷Ⅰ文)甲组有5名男同学、3名女同学;乙组有6名男同学、2名女同学,若从甲、乙两组中各选出2名同学,则选出的4人中恰有1名女同学的不同选法共有
(A)150种 (B)180种 (C)300种 (D)345种
[解析]本小题考查分类计算原理、分步计数原理、组合等问题,基础题。
解:由题共有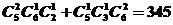 ,故选择D。
,故选择D。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com