
2、条件:Σ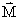 = 0 ,或ΣM+ =ΣM-
= 0 ,或ΣM+ =ΣM- 
如果物体静止,肯定会同时满足两种平衡,因此用两种思路均可解题。
1、特征:物体无转动加速度。
2、条件:Σ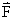 = 0 ,或
= 0 ,或 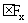 = 0 ,
= 0 ,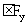 = 0
= 0
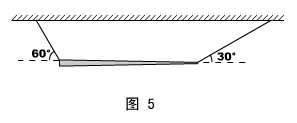 例题:如图5所示,长为L 、粗细不均匀的横杆被两根轻绳水平悬挂,绳子与水平方向的夹角在图上已标示,求横杆的重心位置。
例题:如图5所示,长为L 、粗细不均匀的横杆被两根轻绳水平悬挂,绳子与水平方向的夹角在图上已标示,求横杆的重心位置。
解说:直接用三力共点的知识解题,几何关系比较简单。
答案:距棒的左端L/4处。
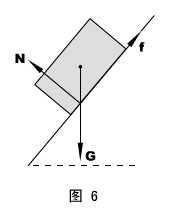 (学生活动)思考:放在斜面上的均质长方体,按实际情况分析受力,斜面的支持力会通过长方体的重心吗?
(学生活动)思考:放在斜面上的均质长方体,按实际情况分析受力,斜面的支持力会通过长方体的重心吗?
解:将各处的支持力归纳成一个N ,则长方体受三个力(G 、f 、N)必共点,由此推知,N不可能通过长方体的重心。正确受力情形如图6所示(通常的受力图是将受力物体看成一个点,这时,N就过重心了)。
答:不会。
1、特征:质心无加速度。
2、按需要--正交分解

第二讲 物体的平衡

1、按效果分解
2、一般平行四边形的合力与分力的求法
余弦定理(或分割成RtΔ)解合力的大小
正弦定理解方向
1、平行四边形法则与矢量表达式
3、乘法
矢量的乘法有两种:叉乘和点乘,和代数的乘法有着质的不同。
 ⑴ 叉乘
⑴ 叉乘
表达: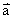 ×
×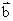 =
= 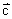

名词: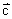 称“矢量的叉积”,它是一个新的矢量。
称“矢量的叉积”,它是一个新的矢量。
叉积的大小:c = absinα,其中α为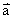 和
和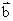 的夹角。意义:
的夹角。意义: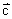 的大小对应由
的大小对应由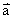 和
和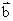 作成的平行四边形的面积。
作成的平行四边形的面积。
叉积的方向:垂直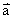 和
和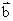 确定的平面,并由右手螺旋定则确定方向,如图4所示。
确定的平面,并由右手螺旋定则确定方向,如图4所示。
显然,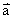 ×
×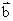 ≠
≠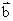 ×
×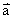 ,但有:
,但有: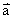 ×
×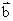 = -
= -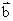 ×
×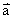

⑵ 点乘
表达: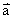 ·
·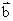 = c
= c
名词:c称“矢量的点积”,它不再是一个矢量,而是一个标量。
点积的大小:c = abcosα,其中α为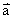 和
和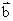 的夹角。
的夹角。
2、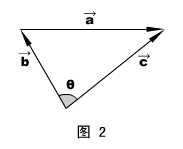 减法
减法
表达: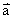 =
= 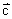 -
-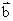 。
。
名词: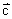 为“被减数矢量”,
为“被减数矢量”,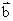 为“减数矢量”,
为“减数矢量”,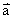 为“差矢量”。
为“差矢量”。
法则:三角形法则。如图2所示。将被减数矢量和减数矢量的起始端平移到一点,然后连接两时量末端,指向被减数时量的时量,即是差矢量。
差矢量大小:a =  ,其中θ为
,其中θ为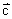 和
和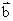 的夹角。
的夹角。
差矢量的方向可以用正弦定理求得。
一条直线上的矢量运算是平行四边形和三角形法则的特例。
例题:已知质点做匀速率圆周运动,半径为R ,周期为T ,求它在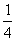 T内和在
T内和在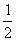 T内的平均加速度大小。
T内的平均加速度大小。
解说:如图3所示,A到B点对应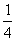 T的过程,A到C点对应
T的过程,A到C点对应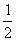 T的过程。这三点的速度矢量分别设为
T的过程。这三点的速度矢量分别设为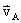 、
、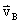 和
和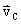 。
。
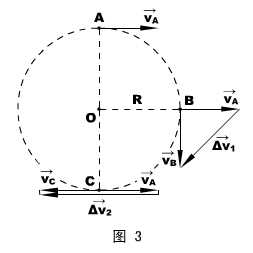 根据加速度的定义
根据加速度的定义 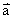 =
= 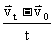 得:
得: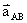 =
= 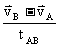 ,
,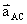 =
= 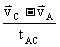

由于有两处涉及矢量减法,设两个差矢量 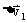 =
=  -
- ,
,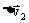 =
= 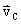 -
-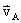 ,根据三角形法则,它们在图3中的大小、方向已绘出(
,根据三角形法则,它们在图3中的大小、方向已绘出(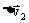 的“三角形”已被拉伸成一条直线)。
的“三角形”已被拉伸成一条直线)。
本题只关心各矢量的大小,显然:
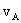 =
= 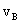 =
= 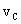 =
= 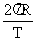 ,且:
,且: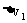 =
= 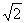
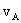 =
= 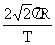 ,
,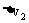 = 2
= 2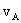 =
= 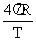

所以: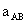 =
= 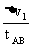 =
= 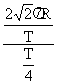 =
= 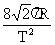 ,
,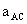 =
= 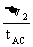 =
= 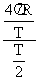 =
= 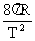 。
。
(学生活动)观察与思考:这两个加速度是否相等,匀速率圆周运动是不是匀变速运动?
答:否;不是。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com