
4.当m+n=p+q(m、n、p、q∈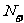 )时,对等差数列{an}有:am+an=ap+aq;对等比数列{an}有:aman=apaq;
)时,对等差数列{an}有:am+an=ap+aq;对等比数列{an}有:aman=apaq;
3.等差数列中, am=an+ (n-m)d, 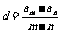 ; 等比数列中,an=amqn-m;
; 等比数列中,an=amqn-m;
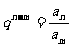
1.首项为正(或负)的递减(或递增)的等差数列前n项和的最大(或最小)问题,转化为解不等式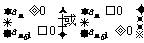 解决;
解决;
2.熟记等差、等比数列的定义,通项公式,前n项和公式,在用等比数列前n项和公式时,勿忘分类讨论思想;
1. 数学应用问题的教学已成为中学数学教学与研究的一个重要内容.解答数学应用问题的核心是建立数学模型,有关平均增长率、利率(复利)以及等值增减等实际问题,需利用数列知识建立数学模型.
7.在等比数列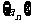 中,
中,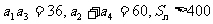 ,求
,求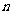 的范围。
的范围。
§4.3数列的综合应用
6.是否存在数列{an},其前项和Sn组成的数列{Sn}也是等比数列,且公比相同?
5.已知数列{an}中,a1=-2且an+1=Sn,求an ,Sn
4.设数列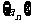 为
为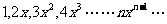
 求此数列前
求此数列前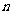 项的和。
项的和。
3.已知无穷数列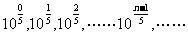 ,
,
求证:(1)这个数列成等比数列
(2)这个数列中的任一项是它后面第五项的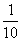 ,
,
(3)这个数列的任意两项的积仍在这个数列中。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com