
4.以下给出的是用条件语句编写的一个伪代码,该伪代码的功能是 .
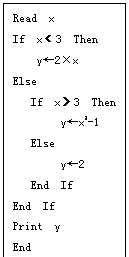
答案 求下列函数当自变量输入值为x时的函数值f(x),其中f(x)=
3.写出下列伪代码的运行结果.

图1 图2
(1)图1的运行结果为 ;
(2)图2的运行结果为 .
答案 (1)7 (2)6
2.为了在运行下面的伪代码后输出y=16,应输入的整数x的值是 .
Read x
If x<0 Then
y←(x+1)2
Else
y←1-x2
End If
Print y
答案 -5
1.伪代码
a←3
b←5
Print a+b
的运行结果是 .
答案 8
12.(2009·青岛模拟)对于函数f(x)=bx3+ax2-3x.
(1)若f(x)在x=1和x=3处取得极值,且f(x)的图象上每一点的切线的斜率均不超过2sintcost-2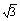 cos2t+
cos2t+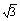 ,试求实数t的取值范围;
,试求实数t的取值范围;
(2)若f(x)为实数集R上的单调函数,且b≥-1,设点P的坐标为(a,b),试求出点P的轨迹所围成的图形的面积S.
解 (1)由f(x)=bx3+ax2-3x,
则f′(x)=3bx2+2ax-3,
∵f(x)在x=1和x=3处取得极值,
∴x=1和x=3是f′(x)=0的两个根且b≠0.


 .
.
∴f′(x)=-x2+4x-3.
∵f(x)的图象上每一点的切线的斜率不超过
2sintcost-2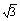 cos2t+
cos2t+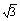 ,
,
∴f′(x)≤2sintcost-2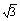 cos2t+
cos2t+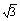 对x∈R恒成立,
对x∈R恒成立,
而f′(x)=-(x-2)2+1,其最大值为1.
故2sintcost-2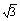 cos2t+
cos2t+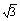 ≥1
≥1
 2sin(2t-
2sin(2t-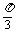 )≥1
)≥1 2k
2k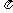 +
+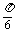 ≤2t-
≤2t-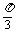 ≤2k
≤2k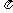 +
+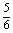
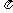 ,k∈Z
,k∈Z
 k
k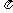 +
+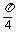 ≤t≤k
≤t≤k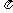 +
+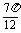 ,k∈Z.
,k∈Z.
(2)当b=0时,由f(x)在R上单调,知a=0.
当b≠0时,由f(x)在R上单调
 f′(x)≥0恒成立,或者f′(x)≤0恒成立.
f′(x)≥0恒成立,或者f′(x)≤0恒成立.
∵f′(x)=3bx2+2ax-3,
∴Δ=4a2+36b≤0可得b≤-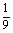 a2.
a2.
从而知满足条件的点P(a,b)在直角坐标平面aOb上形成的轨迹所围成的图形是由曲线b=-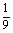 a2与直线b=-1所围成的封闭图形,
a2与直线b=-1所围成的封闭图形,
其面积为S=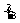 (1-
(1-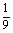 a2)da=4.
a2)da=4.
11.已知f(a)= 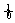 (2ax2-a2x)dx,求f(a)的最大值.
(2ax2-a2x)dx,求f(a)的最大值.
解 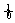 (2ax2-a2x)dx=(
(2ax2-a2x)dx=(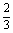 ax3-
ax3-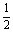 a2x2)|
a2x2)|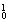 =
=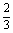 a -
a -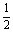 a2
a2
即f(a)= 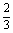 a-
a-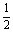 a2=-
a2=-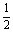 (a2-
(a2-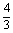 a+
a+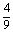 )+
)+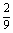
=-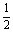 (a-
(a-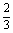 )2+
)2+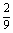 .
.
所以当a=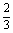 时,f(a)有最大值
时,f(a)有最大值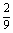 .
.
10.已知f(x)=ax2+bx+c,且f(-1)=2,f′(0)=0,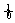 f(x)dx=-2,求a、b、c的值.
f(x)dx=-2,求a、b、c的值.
解 由f(-1)=2,得a-b+c=2, ①
又f′(x)=2ax+b,
由f′(0)=0得b=0, ②
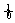 f(x)dx=
f(x)dx=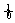 (ax2+bx+c)dx
(ax2+bx+c)dx
=(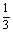 ax3+
ax3+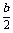 x2+cx)|
x2+cx)|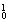
=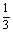 a+
a+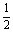 b+c.
b+c.
即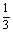 a+
a+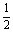 b+c=-2, ③
b+c=-2, ③
由①②③得:a=6,b=0,c=-4.
9.求下列定积分的值
(1) 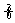
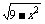 dx;
dx;
(2)已知f(x)= ,求
,求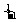 f(x)dx的值.
f(x)dx的值.
解 (1)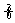
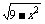 dx表示以y=
dx表示以y=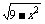 与x=0,x=3所围成图形的面积,而y=
与x=0,x=3所围成图形的面积,而y=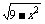 与x=0,x=3围成的图形为圆x2+y2=9在第一象限内的部分,因此所求的面积为
与x=0,x=3围成的图形为圆x2+y2=9在第一象限内的部分,因此所求的面积为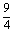
 .
.
(2)∵f(x)=
∴ f(x)dx=
f(x)dx=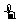 x2dx+
x2dx+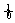 1dx
1dx
=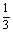 x3|
x3|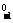 +x|
+x|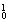 =
=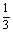 +1=
+1=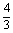 .
.
8.定积分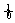
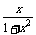 dx的值是 .
dx的值是 .
答案 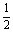 ln2
ln2
7.若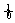 f(x)dx=1,
f(x)dx=1, 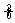 f(x)dx=-1,则
f(x)dx=-1,则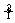 f(x)dx=
.
f(x)dx=
.
答案 -2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com