4.波的叠加与波的干涉

(1)波的叠加原理：在两列波相遇的区域里，每个质点都将参与两列波引起的振动，其位移是两列波分别引起位移的矢量和．相遇后仍保持原来的运动状态．波在相遇区域里，互不干扰，有独立性．

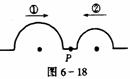[例1]一个波源在绳的左端发出半个波①，频率为f₁，振幅为A₁；同时另一个波源在绳的右端发出半个波②，频率为f₂，振幅为A₂， P为两波源的中点，由图6-18可知，下述说法错误的是(　　　　 )

　　 A．两列波同时到达两波源的中点P

B．两列波相遇时， P点波峰值可达A₁+A₂ 　　

C．两列波相遇后，各自仍保持原来的波形独立传播

　　 D、两列波相遇时，绳上的波峰可达A₁+A₂的点只有一点，此点在P点的左侧

　　 解析：因两列波在同一介质(绳)中传播，所以波速相同，由图可知 λ₁＞λ₂，说明它们的波峰高P点距离不等，波同时传至P点，波峰不会同时到P点，所以P点波峰值小于A₁+ A₂．两列波波峰能同时传到的点应在P点左侧，所以A，D正确，B错误，又由波具有独立性，互不干扰，所以C正确．答案：B

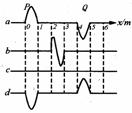[例2]一波源在绳子的左瑞发生波P．另一波源在同一根绳子右端发生波Q，波速为lm／s．在t＝0时绳上的波形如图中的a所示，根据波的叠加原理，以下判断正确的是(　 )

　A．当t＝2s时．波形图如b图．t＝4s时．波形图如c图；

　B．当t＝2s时，波形图如 b图，t＝4s时，波形图如d图　　

　C．当 t＝2s时，波形图如C图，t＝4s时，波形图如b图；

　D．当 t＝2s时，波形图如 C图，t=4s时，波形图如 d图　

解析:由图中的所示的图形来看，b图肯定是不正确的，因为波在同一媒质中传播时的波长是不变，而b图中波长发生了变化，所以选项内容中凡涉及到了b图的情况肯定是不正确的，本题4个选项中只有D选项没有涉及到b图，所以D选项肯定正确．从波的叠加角度来分析，在t＝2s时，两列波均传播了2m，它们刚好重合，由于它们是波峰和波谷相遇，所以叠加的结果是相遇后的质点位移均为零，C图是正确的，当t＝4s时，两列波均传播了4m的距离，相当于在a图的位置上互换，d图是正确的．所以D选项正确．

点评：本题的关键是扣住在同一媒质中，波传播过程中波形不变以及传播的距离与时间的关系．

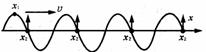
[例3]两列简谐波均沿x轴传播，传播速度的大小相等，其中一列沿x轴正方向传播，如图32中实线所示。一列波沿x负方向传播，如图32中虚线所示。这两列波的频率相等，振动方向均沿y轴，则图中x=1,2,3,4,5,6,7,8各点中振幅最大的是x=　　　　　 的点，振幅最小的是x=　　　　　　 的点。

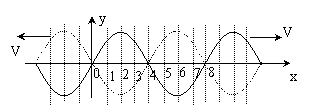解析:对于x=4、8的点，此时两列波引起的位移的矢量和为零，但两列波引起的振动速度的矢量和最大，故应是振动最强的点，即振幅最大的点。对于x=2和6的点，此时两列波引起的位移矢量和为零，两列波引起的振动速度的矢量和也为零，故应是振动最弱的点，即振幅最小的点。

　(2)波的干涉:

①条件：频率相同的两列同性质的波相遇．

②现象：某些地方的振动加强，某些地方的振动减弱，并且加强和减弱的区域间隔出现，加强的地方始终加强，减弱的地方始终减弱，形成的图样是稳定的干涉图样．

说明：①加强、减弱点的位移与振幅．

加强处和减弱处都是两列波引起的位移的矢量和，质点的位移都随时间变化，各质点仍围烧平衡位置振动，与振源振动周期相同．

加强处振幅大，等于两列波的振幅之和，即A=A₁ +A₂,质点的振动能量大，并且始终最大．

减弱处振幅小，等于两列波的振福之差，即A=∣A₁－A₂∣,质点振动能量小，并且始终最小，若A₁=A₂，则减弱处不振动．

加强点的位移变化范围： 一∣A₁ +A₂∣-∣A₁ +A₂∣

减弱点位移变化范围：一∣A₁－A₂∣-∣A₁－A₂∣

②干涉是波特有的现象．

③加强和减弱点的判断．

波峰与波峰(波谷与波谷)相遇处一定是加强的，并且用一条直线将以上加强点连接起来，这条直线上的点都是加强的；而波峰与波谷相遇处一定是减弱的，把以上减弱点用直线连接起来，直线上的点都是减弱的．加强点与减弱点之间各质点的振幅介于加强点与减弱点振幅之间．

当两相干波源振动步调相同时，到两波源的路程差Δs是波长整数倍处是加强区．而路程差是半波长奇数倍处是减弱区．

任何波相遇都能叠加，但两列频率不同的同性质波相遇不能产生干涉．

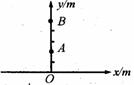[例4]如图所示，在坐标xoy的y轴上有两个相同的波源A、B，它们激起水波波长为2m，A、B的坐标分别为(0，2m)和(0，5m)．在x轴上从－∞到十∞范围内两列波叠加相减弱的点的个数为多少个？

[解析]在X轴上任取点C，连接CA、CB．如图所示，由图可知CB－CA≤AB＝3m(由三角形任意两边之差小于第三边原理得出左式)，所以(CB－CA)的值可以取lm、2m、3m．而A、B两波源激起的水波波长为2m，则只有当(CB－CA)值为半波长的奇数倍时，两列波相遇才是减弱的，故取lm、3m时两列波叠加后是减弱的，由于是在x轴上从－∞到十∞范围内寻找，以及关于y轴对称的关系，故减弱点共有3个．

[例5]两列振动情况完全相同的振源。S₁和s₂在同一个介质中形成机械波。某时刻两列波叠加的示意图如图所示，图中实线表示处于波峰的各质点，虚线表示处于波谷的各质点。图中a、b、c三点中，振动情况加强的质点有　　　　 ，振动情况减弱的质点有　　 。

解析:在两列波叠加的区域内，图中a点是实线与实线的交点，表明两列波都要求a点为正向位移，a点的位移是两列波位移的矢量之和，即振幅之和，是振动情况加强的质点。同样处于虚线与虚线交点的b质点，也是振动情况加强的点。只是b是处于反向最大位移(也等于两列波振幅之和)。因此处于实线与虚线交点的质点c是振动情况减弱的质点，其此刻位移为零。

本题叠加的两列波是波长(频率)相同的两列波，满足干涉的条件。过半个周期，图中实线变为虚线，虚线变为实线。a、b仍是振动情况加强的点，c点仍是振动情况减弱的点。即a、b以两列波振幅的和为振幅振动，C点则以它们振幅之差为振幅振动，且加强点与减弱点间隔排列。

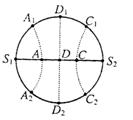[例6]如图所示，在同一均匀媒质中有S₁、S₂两个波源，这个波源的频率、振动方向均相同，且振动的步调完全一致，S₁、S₂之间相距两个波长，D点为S₁、S₂连线中点，今以D点为圆心，以R=DS₁为半径画圆，问在该圆周上(S₁、S₂两波源除外)共有几个加强点？

分析：干涉强、弱区的判断方法有两种：

(1)在波峰与波峰相遇或波谷与波谷相遇处是干涉加强区；在波峰与波谷相遇或波谷与波峰相遇处是干涉减弱区。

(2)与相同波源的距离差为半波长的偶数倍处是干涉加强区；与相同波源的距离差为半波长的奇数倍处是干涉减弱区。

解答：由干涉强、弱的第二种判断方法可知，干涉加强区的集合实际上是以两波源所在处为焦点的双曲线簇。由此不难判断：以波源边线为直径的贺周上分布看，到两波源距离差等于0的两个加强是D₁、D₂；到两波源距离差等于的四个加强是A₁、A₂、C₁、C₂。即：除两波源外，圆周上振动加强是共有六个。

[例7]如图所示，在半径为R=45m的圆心O和圆周A处，有两个功率差不多的喇叭，同时发出两列完全相同的声波，且波长=10m。若人站在B处，正好听不到声音；若逆时针方向从B走到A，则时而听到时而听不到声音。试问在到达A点之前，还有几处听不到声音？　　　　　　　　　　　　　　　　　　　　　　　　　　　　

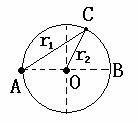解析：因为波源A、O到B点的波程差为Δr=r₁-r₂=R=45m=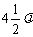，所以B点发生干涉相消现象。

在圆周任一点C上听不到声音的条件为：

Δr = r₁-r₂ =±(2k+1)λ/2=±5(2k+1)

将r₂=R=45m代入上式得：r₁=±5(2k+1)+ r₂

所以：r₁=10k+50　 或　 r₁= -10k+40

而0 < r₁ < 90m，所以有：0 <(10k+50) < 90m 和　 0 <(-10k+40) < 90m

求得 :-5 < k < 4

即k = -4、-3、-2、-1、0、1、2、3，所以在到达A点之前有八处听不到声音。

3.波的衍射:波可以绕过障碍物继续传播的现象．

衍射是波的特性，一切波都能发生衍射．

产生明显衍射现象的条件是：障碍物或孔的尺寸比波长小或与波长相差不多。

例如：声波的波长一般比院坡大，“隔堵有耳”就是声波衍射的例证．

说明：衍射是波特有的现象．

2.波的折射: 波从一种介质射入另一种介质时，传播方向发生改变的现象．

(1)波的折射中，波的频率不变，波速和波长都发生了改变．

(2)折射角：折射波的波线与界面法线的夹角．

(3)入射角i与折射角r的关系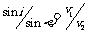

　　 V₁和v₂是波在介质I和介质Ⅱ中的波速．i为I介质中的入射角,r为Ⅱ介质中的折射角．

1.波的反射:波遇到障碍物会返回来继续传播的现象．

(1)波面：沿波传播方向的波峰(或波谷)在同一时刻构成的面．

(2)波线：跟波面垂直的线，表示波的传播方向．

(3)入射波与反射波的方向关系．

①入射角：入射波的波线与平面法线的夹角．

② 反射角：反射波的波线与平面法线的夹角．

③在波的反射中，反射角等于入射角；反射波的波长、频率和波速都跟入射波的相同．

(4)特例：夏日轰鸣不绝的雷声；在空房子里说话会听到声音更响．

(5)人耳能区分相差0.1 s以上的两个声音．

5.介质中质点的振动方向未定

　　 在波的传播过程中，质点振动方向与传播方向联系，若某一质点振动方向未确定，则波的传播方向有两种，这样形成多解．

　　 说明：波的对称性：波源的振动要带动它左、右相邻介质点的振动，波要向左、右两方向传播．对称性是指波在介质中左、右同时传播时，关于波源对称的左、右两质点振动情况完全相同．

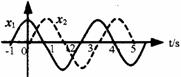[例3]一列在x轴上传播的简谐波，在x_l= 10cm和x₂=110cm处的两个质点的振动图象如图所示，则质点振动的周期为　　　　　　 s，这列简谐波的波长为　　　　 cm．

　 [解析]由两质点振动图象直接读出质点振动周期为 4s．由于没有说明波的传播方向，本题就有两种可能性：(1)波沿x轴的正方向传播．在t＝0时，x₁在正最大位移处，x₂在平衡位置并向y轴的正方向运动，那么这两个质点间的相对位置就有如图所示的可能性，也就x₂一 x₁＝(n十1/4)λ，λ=400/(1十4n)cm

(2)波沿x轴负方向传播．在t＝0时．x₁在正最大位移处，x₂在平衡位置并向y轴的正方向运动，那么这两个质点间的相对位置就有如图所示的可能性……，x₂一 x₁＝(n十3/4)λ，λ=400／(3+ 4n)cm　　　　　

点评：由于波在媒质中传播具有周期性的特点，其波形图每经过一个周期将重复出现以前的波形图，所以由媒质中的质点的振动图象确定波长的值就不是唯一的(若要是唯一的，就得有两个前提：一个是确定波传播方向；一个是确定波长的范围)．

[例4]如图实线是某时刻的波形图象，虚线是经过0.2s时的波形图象。求：

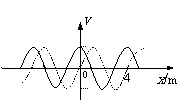①波传播的可能距离 ②可能的周期(频率)

③可能的波速　 ④若波速是35m/s，求波的传播方向　

⑤若0.2s小于一个周期时，传播的距离、周期(频率)、波速。

解析：

①题中没给出波的传播方向，所以有两种可能：向左传播或向右传播。

向左传播时，传播的距离为x=nλ+3λ/4=(4n+3)m　 (n=0、1、2　 …)

向右传播时，传播的距离为x=nλ+λ/4=(4n+1)m　 (n=0、1、2　 …)

②向左传播时，传播的时间为t=nT+3T/4得：T=4t/(4n+3)=0.8 /(4n+3)(n=0、1、2　 …)

向右传播时，传播的时间为t=nT+T/4得：T=4t/(4n+1)=0.8 /(4n+1)　 (n=0、1、2　 …)

③计算波速，有两种方法。v=x/t　 或v=λ/T

向左传播时，v=x/t=(4n+3)/0.2=(20n+15)m/s. 或v=λ/T=4 (4n+3)/0.8=(20n+15)m/s.(n=0、1、2　 …)

向右传播时，v=x/t=(4n+1)/0.2=(20n+5)m/s. 或v=λ/T=4 (4n+1)/0.8=(20n+5)m/s. (n=0、1、2　 …)

④若波速是35m/s，则波在0.2s内传播的距离为x=vt=35×0.2m=7m=1λ，所以波向左传播。

⑤若0.2s小于一个周期，说明波在0.2s内传播的距离小于一个波长。则：

向左传播时，传播的距离x=3λ/4=3m；传播的时间t=3T/4得：周期T=0.267s；波速v=15m/s.向右传播时，传播的距离为λ/4=1m；传播的时间t=T/4得：周期T=0.8s；波速v =5m/s.

点评：做此类问题的选择题时，可用答案代入检验法。

[例5]如图所示，一列简谐横波在t₁时刻的波形，如图甲所示，质点P在该时刻的振动速度为v，t₂时刻质点P的振动速度与t₁时刻的速度大小相等，方向相同；t₃时刻质点P的速度与t₁时刻的速度大小相等，方向相反．若t₂－t₁＝t₃-t₂＝0．2秒，求这列波的传播速度．

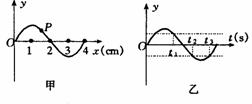　　 解析：从振动模型分析，若质点P从t₁时刻开始向平衡位置方向振动，在一个周期内，从t₁时刻到t₂时刻，从t₂时刻到t₃时刻，对应的振动图象如图乙所示．考虑到振动的周期性，则有：　 t₂-t₁＝(n+1／4)T　　　 n＝0，1，2……

　 周期为：T=(t₂一t₁)／(n十1/4)　 n＝0，1，2……

　 由公式：v＝λ／T　 得出速度v的通解为： v＝20(n+l／4) n=0，1，2……方向向左．

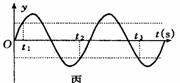　 若质点 P从 t₁时刻开始背离平衡位置方向振动，在一个周期内，从t₁时刻到t2时刻，从t₂时刻到t₃时刻，对应的振动图象如图丙所示．考虑到振动的周期性，则有：

　 t₂-t₁＝(n+3／4)T　　　 n＝0，1，2……

　 周期为：T=(t₂一t₁)／(n十3/4)　 n＝0，1，2……

　 由公式：v＝λ／T　 得出速度v的通解为： v＝20(n+3／4) n=0，1，2……方向向右．

　 答案：v＝20(n+l／4)(n＝0，1，2……)　　 方向向左．

　　 或v＝ 20( n+ 3／4)( n＝ 0，1，2，……)方向向右

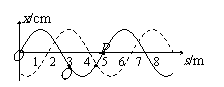[例6]已知在t₁时刻简谐横波的波形如图中实线所示；在时刻t₂该波的波形如图中虚线所示。t₂-t₁ = 0.02s来求：⑴该波可能的传播速度。⑵若已知T< t₂-t₁<2T，且图中P质点在t₁时刻的瞬时速度方向向上，求可能的波速。⑶若0.01s<T<0.02s，且从t₁时刻起，图中Q质点比R质点先回到平衡位置，求可能的波速。

解：⑴如果这列简谐横波是向右传播的，在t₂-t₁内波形向右匀速传播了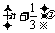，所以波速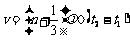=100(3n+1)m/s (n=0,1,2,…)；同理可得若该波是向左传播的，可能的波速v=100(3n+2)m/s　 (n=0,1,2,…)

　　 ⑵P质点速度向上，说明波向左传播，T< t₂-t₁ <2T，说明这段时间内波只可能是向左传播了5/3个波长，所以速度是唯一的：v=500m/s

　　 ⑶“Q比R先回到平衡位置”，说明波只能是向右传播的，而0.01s<T<0.02s，也就是T<0.02s<2T，所以这段时间内波只可能向右传播了4/3个波长，解也是唯一的：v=400m/s

[例7]一列横波沿直线在空间传播，某一时刻直线上相距为d的M、N两点均处在平衡位置，且M、N之间仅有一个波峰，若经过时间t，N质点恰好到达波峰位置，则该列波可能的波速是多少？

分析与解：本题没有给定波的传播方向，仅告诉我们在某一时刻M、N两点均处在平衡位置，且M、N之间仅有一个波峰．由此我们可以推想，处在直线MN上的各个质点在该时刻相对平衡位置的位移可能会有以下四种情况，即波的图像有以下四种图形(如图中A、B、C、D图，各图中均为左端为M，右端为N)：

若波的传播方向由M到N，那么：

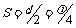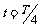　　 在A图中，经过时间t，N恰好到达波峰，说明时间t内波向右前进的距离，且，所以波速．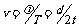

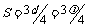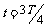　　 在B图中，经过时间t，波峰传到N点，则波在时间t内向右前进的距离，且，所以波速．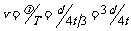

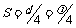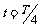　　 在C图中，经过时间t，波向右前进的距离，且，所以波速．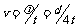

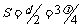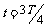　　 在D图中，经过时间t，波向右前进的距离，且，所以波速．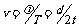

　　 若波的传播方向从N到M，那么：

　 　在A图中，质点N此时要向下振动，经过时间t，N到达波峰，则时间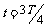，在时间t内波向左前进的距离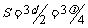，所以波速．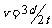

　　 在B图中，经过时间t， N到达波峰，则时间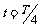，在此时间内波向左前进的距离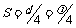，所以波速．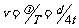

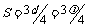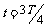　　 在C图中，波在时间t内向左前进的距离，且，所以波速．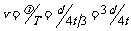

　　 在D图中，质点N经过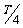变为波峰，所以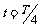，在时间t内波向左前进的距离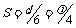，所以波速．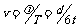

所以该列波可能的波速有五种、、、、．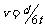

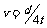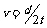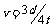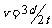　其实上述解决问题的方法过于程序化，如果能够判断出八种情况下该时刻波形图上的波峰在传播方向上到N点的距离S，波速v就等于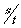．例如：最后一种情况中，波峰在传播方向上到N点的距离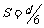，所以波速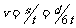．其它情况读者可自行解决．

规律方法

试题展示

波的现象与声波

知识简析　 一、波的现象

4.介质中两质点间的距离与波长关系未定

　　 在波的传播方向上，如果两个质点间的距离不确定，就会形成多解，解题时若不能联想到所有可能情况，易出现漏解．

3.波的双向性

　　 双向性是指波沿正负方向传播时，若正、负两方向的传播时间之和等于周期的整数倍，则沿正负两方向传播的某一时刻波形相同．

2.波的时间的周期性

　　 在x轴上同一个给定的质点，在t+nT时刻的振动情况与它在t时刻的振动情况(位移、速度、加速度等)相同．因此，在t时刻的波形，在t+nT时刻会多次重复出现．这就是机械波的时间的周期性．

波的时间的周期性，表明波在传播过程中，经过整数倍周期时，其波的图象相同．

波动图象的多解涉及：(1)波的空间的周期性；(2)波的时间的周期性；(3)波的双向性；(4)介质中两质点间距离与波长关系未定；(5)介质中质点的振动方向未定．

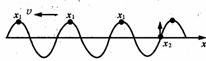
1.波的空间的周期性

　　 沿波的传播方向，在x轴上任取一点P(x)，如图所示，P点的振动完全重复波源O的振动，只是时间上比O点要落后Δt，且Δt =x/v=xT₀/λ.在同一波线上，凡坐标与P点坐标x之差为波长整数倍的许多质点，在同一时刻t的位移都与坐标为λ的质点的振动位移相同，其振动速度、加速度也与之相同，或者说它们的振动“相貌”完全相同．因此，在同一波线上，某一振动“相貌”势必会不断重复出现，这就是机械波的空间的周期性．

　 　空间周期性说明，相距为波长整数倍的多个质点振动情况完全相同．