
15.在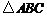 中,已知
中,已知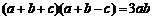 ,且
,且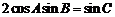 .判断
.判断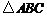 的形状.
的形状.
解: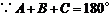 ,
, .
.
又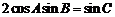 ,
,
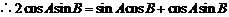 ,
,
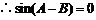 .
.
又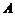 与
与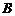 均为
均为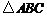 的内角,
的内角,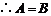 .
.
又由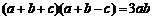 ,
,
得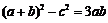 ,
,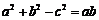 ,
,
又由余弦定理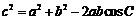 ,
,
得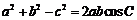 ,
,
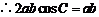 ,
,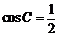 ,
,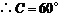 .
.
又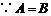 ,
,
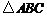 为等边三角形.
为等边三角形.
14.用分析法证明:若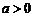 ,则
,则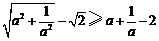 .
.
解:要证原不等式,只需证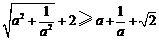 .
.
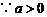 ,
, 两边均大于零.
两边均大于零.
因此只需证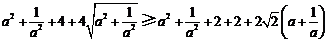 ,
,
只需证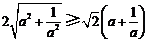 ,
,
只需证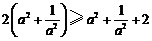 ,即证
,即证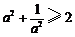 ,而
,而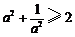 显然成立,
显然成立,
 原不等式成立.
原不等式成立.
13.设函数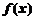 对任意
对任意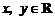 ,都有
,都有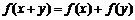 ,
, 且
且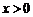 时,
时,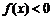 .
.
(1)证明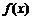 为奇
为奇 函数;
函数;
(2)证明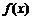 在
在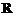 上为减函数.
上为减函数.
证明:(1)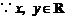 ,
,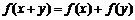 ,
,
 令
令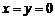 ,
,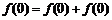 ,
,
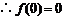 ,令
,令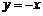 ,代入
,代入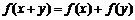 ,得
,得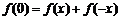 ,
,
而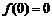 ,
,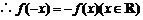 ,
,
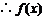 是奇函数;
是奇函数;
(2)任取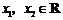 ,且
,且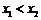 ,
,
则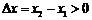 ,
,
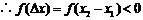 .
.
又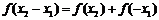 ,
,
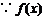 为奇函数,
为奇函数,
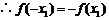 ,
,
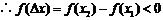 ,即
,即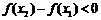 ,
,
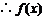 在
在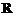 上是减函数.
上是减函数.
12.向量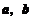 满足
满足
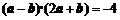 ,且
,且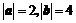 ,则
,则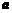 与
与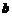 夹角的余弦值等于 .
夹角的余弦值等于 .
 答案:
答案: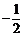
11.已知平面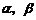 和直线
和直线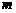 ,给出条件:①
,给出条件:①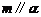 ;
; ②
②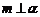 ;③
;③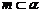 ;④
;④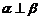 ;⑤
;⑤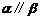 .(1)当满足条件 时,有
.(1)当满足条件 时,有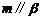 ,(2)当满足条件 时,有
,(2)当满足条件 时,有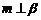 .(填所选条件的序号)
.(填所选条件的序号)
答案:③⑤,②⑤
10.已知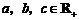 ,且
,且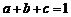 ,求证:
,求证: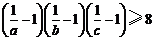 .
.
证明过程如下:

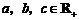 ,且
,且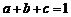 ,
,
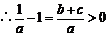 ,
,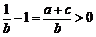 ,
,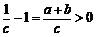 ,
,
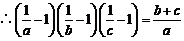 .
.
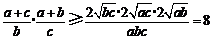 ,
,
当且仅当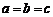 时取等号,
时取等号, 不等式成立.
不等式成立.
这种证法是 .(综合法、分析法或反证法)
答案:综合法
9.若抛物线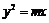 与椭圆
与椭圆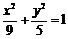 有一个共同的焦点,则
有一个共同的焦点,则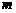
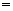 .
.
答案 :
: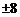
8.三次函数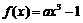 在
在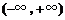 内是减函数,则
内是减函数,则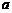 的取值范围是 .
的取值范围是 .
答案: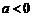
7.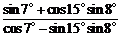 的值为 .
的值为 .
答案: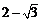
6.已知函数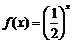 ,
,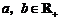
 ,
,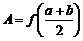 ,
,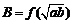 ,
,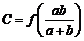 ,则
,则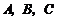 的大小关系( )
的大小关系( )
A.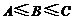 B.
B.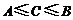 C.
C.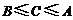 D.
D.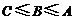
答案:A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com