
13.(09重庆)许多同学都很喜欢设计和参加“多米诺骨牌效应”活动(按一定距离拌列的骨牌,碰倒第一块骨牌后,其它所有骨牌会依次倒下),其中的物理原理是:骨牌倒下时,
转化为 ,这部分能量就转移给下一张骨牌,下一张骨牌倒下时具有的能量更大,骨牌被推倒的速度越来越快。(选填“动能”、“重力势能”)
答案:重力势能 动能

22.已知函数 .
.
(Ⅰ)解关于x的方程: ;
;
(Ⅱ)记 ,
, 的最大、最小值构成的集合为
的最大、最小值构成的集合为 ,又
,又 ,
, ,对于任意常数
,对于任意常数 ,方程
,方程 在区间
在区间 上有且只有两个根,试求函数
上有且只有两个根,试求函数 的单调增区间.
的单调增区间.
解:(Ⅰ)
 在
在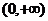 上递减;
上递减;
由于 ,且
,且 在
在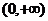 上递减;
上递减;
故: 有且只有一个实数根
有且只有一个实数根 .
.
(Ⅱ)由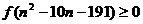 得:
得:
 ;
;
 ;
;
 ;
;
 .
.
由 ,易知
,易知 ;
;
由 得
得 ,又
,又 ,
, ;
;
由于方程 在区间
在区间 上有且只有两个根知
上有且只有两个根知 的最小正周期为
的最小正周期为 ,
,
 ;
;
从而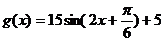 ;
;
由 得
得 ;
;
故函数 的单调增区间
的单调增区间 .
.
21.已知直线l与抛物线 相切于点
相切于点 ,又与抛物线
,又与抛物线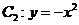 相交于两点A、B. 分别过A、B作
相交于两点A、B. 分别过A、B作 的切线
的切线 ,
, 相交于点Q,设
相交于点Q,设 ,
, ,
, 的斜率分别为
的斜率分别为 .
.
求证:(Ⅰ) 成等差数列;
成等差数列;
(Ⅱ)点Q在 上.
上.
证明:(Ⅰ)设 ,
,
对 求导得
求导得 ;
; ,
,
所以 的方程为
的方程为 ,即
,即 ,代入
,代入 得
得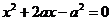 ,
,
 .
.
对 求导得
求导得 ;
; ,
, ;
;
从而 ,
,
所以 成等差数列;
成等差数列;
(Ⅱ) 的方程为
的方程为 ,即
,即 ,
,
 的方程为
的方程为 ,即
,即 ,
,
两式相减得 ,
,
即 ,
,
将 代入
代入 的方程得
的方程得 ,
,
即 ,
,
所以点Q的坐标为 ,显然满足
,显然满足 的方程,
的方程,
故点Q在 上.
上.
20. 设函数 其中
其中 ,
, .当且仅当
.当且仅当 时,函数
时,函数 取得最小值
取得最小值 .
.
(Ⅰ)求函数 的表达式;
的表达式;
(Ⅱ)若方程
 至少有两个不相同的实数根,求
至少有两个不相同的实数根,求 取值的集合.
取值的集合.
解:(Ⅰ)


(Ⅱ)记方程①: 方程②:
方程②:
分别研究方程①和方程②的根的情况:
(1)方程①有且仅有一个实数根 方程①没有实数根
方程①没有实数根
(2)方程②有且仅有两个不相同的实数根,即方程 有两个不相同的非正实数根.
有两个不相同的非正实数根.

方程②有且仅有一个不相同的实数根,即方程 有且仅有一个蜚 正实数根.
有且仅有一个蜚 正实数根.

综上可知:当方程 有三个不相同的实数根时,
有三个不相同的实数根时,
当方程 有且仅有两个不相同的实数根时,
有且仅有两个不相同的实数根时,
 符合题意的实数
符合题意的实数 取值的集合为
取值的集合为
18. 已知函数 ,定义数列
,定义数列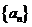 ,使:
,使: ,…,
,…, … .
… .
(1)求证:数列 是等差数列;
是等差数列;
(2)设数列 的前n项和为
的前n项和为 ,求证:
,求证: .
.
解:(1)∵ ∴
∴
∴
又 ∴数列{
∴数列{ }是以
}是以 为首项,以
为首项,以 为公差的等差数列.
为公差的等差数列.
(2)由(1)可知
∴
∴

 .
.
 19:如图,一张平行四边形的硬纸片
19:如图,一张平行四边形的硬纸片 中,
中, ,
, .沿它的对角线
.沿它的对角线 把
把 折起,使点
折起,使点 到达平面
到达平面 外点
外点 的位置.
的位置.
(Ⅰ)证明:平面 平面
平面 ;
;
(Ⅱ)如果△ 为等腰三角形,求二面角
为等腰三角形,求二面角 的大小。
的大小。
解:(Ⅰ)证明:因为 ,
,
 ,所以
,所以 .
.
因为折叠过程中, ,
,
所以 ,又
,又 ,故
,故 平面
平面 .
.
又 平面
平面 ,
,
所以平面 平面
平面 .
.
(Ⅱ)解法一:如图,延长 到
到 ,使
,使 ,连结
,连结 ,
, 。
。
因为

 ,
, ,
, ,
, ,所以
,所以 为正方形,
为正方形, 。
。
 由于
由于 ,
, 都与平面
都与平面 垂直,所以
垂直,所以 ,可知
,可知 。
。
因此只有 时,△
时,△ 为等腰三角形。
为等腰三角形。
在 △
△ 中,
中, ,又
,又 ,
,
所以△ 为等边三角形,
为等边三角形, 。
。
由(Ⅰ)可知,,所以 为二面角
为二面角 的平面角,即二面角
的平面角,即二面角 的大小为
的大小为 。
。
解法二:以 为坐标原点,射线
为坐标原点,射线 ,
, 分别为
分别为 轴正半轴和
轴正半轴和 轴正半轴,建立如图的空间直角坐标系
轴正半轴,建立如图的空间直角坐标系 ,则
,则 ,
, ,
, 。
。
 由(Ⅰ)可设点
由(Ⅰ)可设点 的坐标为
的坐标为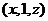 ,其中
,其中 ,则有
,则有 。 ①
。 ①
因为△ 为等腰三角形,所以
为等腰三角形,所以 或
或 。
。
若 ,则有
,则有 。
。
则此得 ,
, ,不合题意。
,不合题意。
若 ,则有
,则有 。
②
。
②
联立①和②得 ,
, 。故点
。故点 的坐标为
的坐标为 。
。
由于 ,
, ,所以
,所以 与
与 夹角的大小等于二面角
夹角的大小等于二面角 的大小。
的大小。
又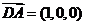 ,
, ,
,
所以 即二面角
即二面角 的大小为
的大小为 。
。
17.已知△ABC的周长为6, 成等比数列.
成等比数列.
(Ⅰ)求 角B及边b的取值范围;
(Ⅱ)求△ABC的面积S的最大值及 的取值范围.
的取值范围.
解:(Ⅰ)设 依次为
依次为 ,则
,则 ,
, ,
,
由余弦定理得 ,
,
故有 ,
,
又 从而
从而 ;
;
(Ⅱ)所以 ,即
,即
所以
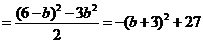
 .
.
16、关于函数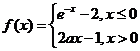 (
( ,且常数
,且常数 )对于下列命题:
)对于下列命题:
①函数 的最小值为-2;
的最小值为-2;
②函数 在每一点处都连续;
在每一点处都连续;
③ ;
;
④函数 在
在 处可导;
处可导;
⑤对任意的实数 且
且 ,恒有
,恒有
其中正确命题的序号是___________________ (②③⑤)
15、若 ,则
,则 的大小关系为
. 答案:
的大小关系为
. 答案:
14、点P是离心率为 ,左、右焦点分别为
,左、右焦点分别为 和
和 的椭圆上一点,且
的椭圆上一点,且 ,
, 的面积为
的面积为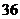 ,则椭圆的方程是
.答案:
,则椭圆的方程是
.答案: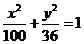 .
.
13、 的值为
.答案:
的值为
.答案: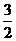
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com