2.写出下列函数极限的值.

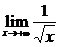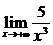(1)； (2)10^x； (3)；(4)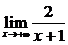

答案：⑴0　 ⑵ 0　　 ⑶ 0　 ⑷ 0

1．1.对于函数y=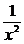，填写下表并画出函数的图象，观察当x→∞时，函数y的变化趋势.

答案：当x→∞时，y=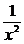无限趋近于0.即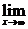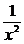=0.

例1分别就自变量x趋向于+∞和－∞的情况,讨论下列函数的变化趋势.

(1)y=(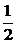)^x

分析：作出这个函数的图象，由图就能看出变化趋势.

解：由图可知，

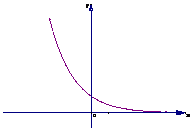
当x→+∞时，y=(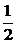)^x无限趋近于0，即　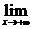(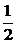)^x=0；

当x→－∞时，y=(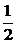)^x无限趋近于+∞.极限不存在．

(2)y=2^x　

解：由图可知，

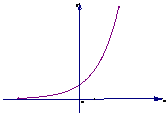
当x→+∞时.y=2^x无限趋近于+∞，极限不存在．

当x→－∞时，y=2^x无限趋近于0，即2^x=0.

　(3)

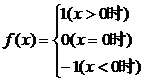
解：由图可知，

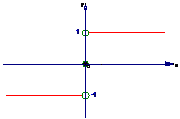
当x→+∞时，f(x)的值为1，即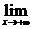f(x)=1;

当x→－∞时，f(x)的值为－1，即f(x)=－1．

说明：当x→+∞时，f(x)不是无限趋近于某个常数a，而是f(x)的值等于常数a，那么函数f(x)当x→+∞时的极限也就是a.x→－∞时，情况也是如此.

3.常数函数f(x)=c.(x∈R)，有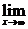f(x)=c.

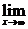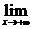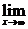注意：f(x)存在，表示f(x)和f(x)都存在，且两者相等.所以f(x)中的∞既有+∞，又有－∞的意义，而数列极限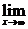a_n中的∞仅有+∞的意义

2.函数极限的定义:

(1)当自变量x取正值并且无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于正无穷大时，函数f(x)的极限是a.

记作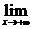：f(x)=a，或者当x→+∞时，f(x)→a.

(2)当自变量x取负值并且绝对值无限增大时，如果函数f(x)无限趋近于一个常数a，就说当x趋向于负无穷大时，函数f(x)的极限是a.

记作f(x)=a或者当x→－∞时，f(x)→a.

(3)如果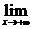f(x)=a且f(x)=a，那么就说当x趋向于无穷大时，函数f(x)的极限是a，

记作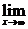：f(x)=a或者当x→∞时，f(x)→a.

1. 举特殊例子

我们先来看函数y=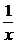(x∈R，x≠0)，画出它的图象，或者列表观察.当x取正值并无限增大，和当x取负值并绝对值无限增大时，函数值的变化趋势.

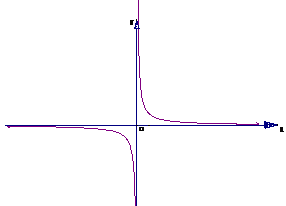
(1)函数 y=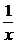 (x∈R，x≠0)的图象：

(2)列表　　 (请学生回答y的值).

从图中或表中可以看出，当x取正值增大时，y的值趋于0；当x取负值并绝对值增大时，y的值也趋于0.

如果也用数列中的极限符号表示：.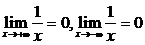

3. 将a_n看成是n的函数即a_n=f(n).自变量n∈N^*，a_n就是一个特殊的函数. 数列的项a_n,随着n的增大a_n越来越接近于a,也就是f(n) 越来越接近于a．

对于一般的函数f(x)，自变量x∈R，是否有同样的结论呢？这节课就来研究当

x→∞时，函数f(x)的极限.

2.几个重要极限：

　 (1)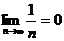　　　　　 (2)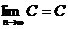(C是常数)

　 (3)无穷等比数列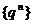(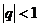)的极限是0，即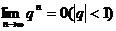 　　

1.数列极限的定义：

　 一般地，如果当项数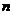无限增大时，无穷数列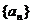的项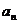无限趋近于某个常数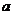(即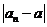无限趋近于0)，那么就说数列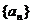以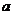为极限，或者说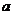是数列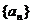的极限．记作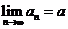，读作“当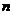趋向于无穷大时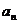，的极限等于”

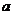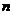
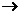“∞”表示“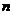趋向于无穷大”，即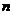无限增大的意思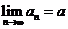有时也记作：当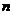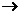∞时，．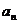

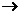
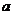理解：数列的极限的直观描述方式的定义，只是对数列变化趋势的定性说明，而不是定量化的定义.“随着项数n的无限增大，数列的项a_n无限地趋近于某个常数a”的意义有两个方面：一方面，数列的项a_n趋近于a是在无限过程中进行的，即随着n的增大a_n越来越接近于a；另一方面，a_n不是一般地趋近于a，而是“无限”地趋近于a，即|a_n－a|随n的增大而无限地趋近于0.

18、(2010·合肥模拟)

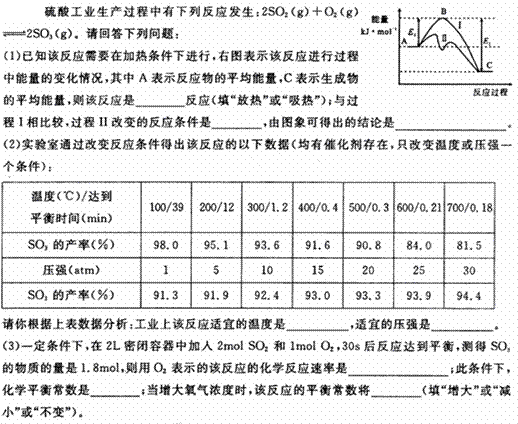
[答案](1)放热　 加入了催化剂　 催化剂可以降低活化能，但不能改变化学反应的反应热

(2)400-500°C　 常压

(3)0.015mol·L^-1 ·S^-1或0.9mol·L^-1 ·min^-1 　　1620 　　不变 　

()