
7.经纬度及球面距离
|
|
|
|
|

 线段AP的长
∠AOP的弧度数 大圆劣弧AP的长
线段AP的长
∠AOP的弧度数 大圆劣弧AP的长
6.棱柱的概念和性质

 ⑴理解并掌握棱柱的定义及相关概念是学好这部分知识的关键,要明确“棱柱 直棱柱 正棱柱”这一系列中各类几何体的内在联系和区别。
⑴理解并掌握棱柱的定义及相关概念是学好这部分知识的关键,要明确“棱柱 直棱柱 正棱柱”这一系列中各类几何体的内在联系和区别。



 ⑵平行六面体是棱柱中的一类重要的几何体,要理解并掌握“平行六面体 直平行六面体 长方体 正四棱柱 正方体”这一系列中各类几何体的内在联系和区别。
⑵平行六面体是棱柱中的一类重要的几何体,要理解并掌握“平行六面体 直平行六面体 长方体 正四棱柱 正方体”这一系列中各类几何体的内在联系和区别。
⑶须从棱柱的定义出发,根据第一章的相关定理对棱柱的基本性质进行分析推导,以求更好地理解、掌握并能正确地运用这些性质。
⑷关于平行六面体,在掌握其所具有的棱柱的一般性质外,还须掌握由其定义导出的一些其特有的性质,如长方体的对角线长定理是一个重要定理并能很好地掌握和应用。还须注意,平行六面体具有一些与平面几何中的平行四边形相对应的性质,恰当地运用平行四边形的性质及解题思路去解平行六面体的问题是一常用的解题方法。
⑸多面体与旋转体的问题离不开构成几何体的基本要素点、线、面及其相互关系,因此,很多问题实质上就是在研究点、线、面的位置关系,与《直线、平面、简单几何体》第一部分的问题相比,唯一的差别就是多了一些概念,比如面积与体积的度量等.从这个角度来看,点、线、面及其位置关系仍是我们研究的重点.
5.空间的距离问题,主要是求空间两点之间、点到直线、点到平面、两条异面直线之间(限于给出公垂线段的)、平面和它的平行直线、以及两个平行平面之间的距离.
求距离的一般方法和步骤是:一作--作出表示距离的线段;二证--证明它就是所要求的距离;三算--计算其值.此外,我们还常用体积法求点到平面的距离.
4.空间的角和距离是空间图形中最基本的数量关系,空间的角主要研究射影以及与射影有关的定理、空间两直线所成的角、直线和平面所成的角、以及二面角和二面角的平面角等.解这类问题的基本思路是把空间问题转化为平面问题去解决.
空间的角,是对由点、直线、平面所组成的空间图形中各种元素间的位置关系进行定量分析的一个重要概念,由它们的定义,可得其取值范围,如两异面直线所成的角θ∈(0, ],直线与平面所成的角θ∈
],直线与平面所成的角θ∈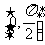 ,二面角的大小,可用它们的平面角来度量,其平面角θ∈
,二面角的大小,可用它们的平面角来度量,其平面角θ∈ 0,π
0,π .
.
对于空间角的计算,总是通过一定的手段将其转化为一个平面内的角,并把它置于一个平面图形,而且是一个三角形的内角来解决,而这种转化就是利用直线与平面的平行与垂直来实现的,因此求这些角的过程也是直线、平面的平行与垂直的重要应用.通过空间角的计算和应用进一步培养运算能力、逻辑推理能力及空间想象能力.
如求异面直线所成的角常用平移法(转化为相交直线)与向量法;求直线与平面所成的角常利用射影转化为相交直线所成的角;而求二面角a-l-b的平面角(记作q)通常有以下几种方法:
(1) 根据定义;
(2) 过棱l上任一点O作棱l的垂面g,设g∩a=OA,g∩b=OB,则∠AOB=q ;
(3) 利用三垂线定理或逆定理,过一个半平面a内一点A,分别作另一个平面b的垂线AB(垂足为B),或棱l的垂线AC(垂足为C),连结AC,则∠ACB=q 或∠ACB=p-q;
(4) 设A为平面a外任一点,AB⊥a,垂足为B,AC⊥b,垂足为C,则∠BAC=q或∠BAC=p-q;
(5) 利用面积射影定理,设平面a内的平面图形F的面积为S,F在平面b内的射影图形的面积为S¢,则cosq=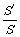 .
.
3.两个平面平行的主要性质:
⑴由定义知:“两平行平面没有公共点”。
⑵由定义推得:“两个平面平行,其中一个平面内的直线必平行于另一个平面。
⑶两个平面平行的性质定理:“如果两个平行平面同时和第三个平面相交,那
么它们的交线平行”。
⑷一条直线垂直于两个平行平面中的一个平面,它也垂直于另一个平面。
⑸夹在两个平行平面间的平行线段相等。
⑹经过平面外一点只有一个平面和已知平面平行。
以上性质⑵、⑷、⑸、⑹在课文中虽未直接列为“性质定理”,但在解题过程中均可直接作为性质定理引用。
2.判定两个平面平行的方法:
(1)根据定义--证明两平面没有公共点;
(2)判定定理--证明一个平面内的两条相交直线都平行于另一个平面;
(3)证明两平面同垂直于一条直线。
1.有关平行与垂直(线线、线面及面面)的问题,是在解决立体几何问题的过程中,大量的、反复遇到的,而且是以各种各样的问题(包括论证、计算角、与距离等)中不可缺少的内容,因此在主体几何的总复习中,首先应从解决“平行与垂直”的有关问题着手,通过较为基本问题,熟悉公理、定理的内容和功能,通过对问题的分析与概括,掌握立体几何中解决问题的规律--充分利用线线平行(垂直)、线面平行(垂直)、面面平行(垂直)相互转化的思想,以提高逻辑思维能力和空间想象能力.
例1.已知 ,求(1)
,求(1) ;(2)
;(2) 的值.
的值.
解:(1) ;
;
(2) 
 .
.
说明:利用齐次式的结构特点(如果不具备,通过构造的办法得到),进行弦、切互化,就会使解题过程简化。
例2.求函数 的值域。
的值域。
解:设 ,则原函数可化为
,则原函数可化为
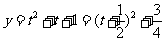 ,因为
,因为 ,所以
,所以
当 时,
时, ,当
,当 时,
时, ,
,
所以,函数的值域为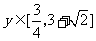 。
。
例3.已知函数 。
。
(1)求 的最小正周期、
的最小正周期、 的最大值及此时x的集合;
的最大值及此时x的集合;
(2)证明:函数 的图像关于直线
的图像关于直线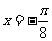 对称。
对称。
解: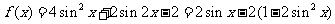

(1)所以 的最小正周期
的最小正周期 ,因为
,因为 ,
,
所以,当 ,即
,即 时,
时, 最大值为
最大值为 ;
;
(2)证明:欲证明函数 的图像关于直线
的图像关于直线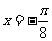 对称,只要证明对任意
对称,只要证明对任意 ,有
,有 成立,
成立,
因为 ,
,
 ,
,
所以 成立,从而函数
成立,从而函数 的图像关于直线
的图像关于直线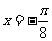 对称。
对称。
例4.
已知函数y= cos2x+
cos2x+ sinx·cosx+1 (x∈R),
sinx·cosx+1 (x∈R),
(1)当函数y取得最大值时,求自变量x的集合;
(2)该函数的图像可由y=sinx(x∈R)的图像经过怎样的平移和伸缩变换得到?
解:(1)y= cos2x+
cos2x+ sinx·cosx+1=
sinx·cosx+1= (2cos2x-1)+
(2cos2x-1)+  +
+ (2sinx·cosx)+1
(2sinx·cosx)+1
= cos2x+
cos2x+ sin2x+
sin2x+ =
= (cos2x·sin
(cos2x·sin +sin2x·cos
+sin2x·cos )+
)+
= sin(2x+
sin(2x+ )+
)+
所以y取最大值时,只需2x+ =
= +2kπ,(k∈Z),即
x=
+2kπ,(k∈Z),即
x= +kπ,(k∈Z)。
+kπ,(k∈Z)。
所以当函数y取最大值时,自变量x的集合为{x|x= +kπ,k∈Z}
+kπ,k∈Z}
(2)将函数y=sinx依次进行如下变换:
(i)把函数y=sinx的图像向左平移 ,得到函数y=sin(x+
,得到函数y=sin(x+ )的图像;
)的图像;
(ii)把得到的图像上各点横坐标缩短到原来的 倍(纵坐标不变),得到函数y=sin(2x+
倍(纵坐标不变),得到函数y=sin(2x+ )的图像;
)的图像;
(iii)把得到的图像上各点纵坐标缩短到原来的 倍(横坐标不变),得到函数y=
倍(横坐标不变),得到函数y= sin(2x+
sin(2x+ )的图像;
)的图像;
(iv)把得到的图像向上平移 个单位长度,得到函数y=
个单位长度,得到函数y= sin(2x+
sin(2x+ )+
)+ 的图像。
的图像。
综上得到y= cos2x+
cos2x+ sinxcosx+1的图像。
sinxcosx+1的图像。
说明:本题是2000年全国高考试题,属中档偏容易题,主要考查三角函数的图像和性质。这类题一般有两种解法:一是化成关于sinx,cosx的齐次式,降幂后最终化成y= sin (ωx+
sin (ωx+ )+k的形式,二是化成某一个三角函数的二次三项式。本题(1)还可以解法如下:当cosx=0时,y=1;当cosx≠0时,y=
)+k的形式,二是化成某一个三角函数的二次三项式。本题(1)还可以解法如下:当cosx=0时,y=1;当cosx≠0时,y= +1=
+1= +1
+1
化简得:2(y-1)tan2x- tanx+2y-3=0
tanx+2y-3=0
∵tanx∈R,∴△=3-8(y-1)(2y-3) ≥0,解之得: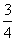 ≤y≤
≤y≤
∴ymax= ,此时对应自变量x的值集为{x|x=kπ+
,此时对应自变量x的值集为{x|x=kπ+ ,k∈Z}
,k∈Z}
例5.已知函数
(Ⅰ)将f(x)写成 的形式,并求其图象对称中心的横坐标;
的形式,并求其图象对称中心的横坐标;
(Ⅱ)如果△ABC的三边a、b、c满足b2=ac,且边b所对的角为x,试求x的范围及此时函数f(x)的值域.
解:
(Ⅰ)由 =0即
=0即
即对称中心的横坐标为
(Ⅱ)由已知b2=ac
 即
即 的值域为
的值域为 .
.
综上所述, ,
,
 值域为
值域为 .
.
说明:本题综合运用了三角函数、余弦定理、基本不等式等知识,还需要利用数形结合的思想来解决函数值域的问题,有利于培养学生的运算能力,对知识进行整合的能力。
例6.在 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且 ,
,
(1)求 的值;
的值;
(2)若 ,且a=c,求
,且a=c,求 的面积。
的面积。
解:(1)由正弦定理及 ,有
,有 ,
,
即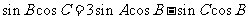 ,所以
,所以 ,
,
又因为 ,
,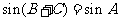 ,所以
,所以 ,因为
,因为 ,所以
,所以 ,又
,又 ,所以
,所以 。
。
(2)在 中,由余弦定理可得
中,由余弦定理可得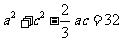 ,又
,又 ,
,
所以有 ,所以
,所以 的面积为
的面积为
 。
。
例7.已知向量
 ,且
,且 ,
,
(1)求函数 的表达式;
的表达式;
(2)若 ,求
,求 的最大值与最小值。
的最大值与最小值。
解:(1) ,
, ,
, ,又
,又 ,
,
所以 ,
,
所以 ,即
,即 ;
;
(2)由(1)可得,令 导数
导数 ,解得
,解得 ,列表如下:
,列表如下:
|
t |
-1 |
(-1,1) |
1 |
(1,3) |
 导数 导数 |
0 |
- |
0 |
+ |
 |
极大值 |
递减 |
极小值 |
递增 |
而 所以
所以 。
。
例8.已知向量 ,
,
(1) 求 的值;
的值;
(2) (2)若 的值。
的值。
解:(1)因为
所以
又因为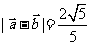 ,所以
,所以 ,
,
即 ;
;
(2)  ,
,
又因为 ,所以
,所以  ,
,
 ,所以
,所以 ,所以
,所以
例9.平面直角坐标系有点
(1)
求向量 和
和 的夹角
的夹角 的余弦用
的余弦用 表示的函数
表示的函数 ;
;
(2)
求 的最值.
的最值.
解:(1)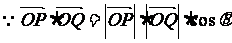 ,
,

即 

(2) , 又
, 又 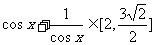 ,
,
 ,
,  ,
,  .
.
说明:三角函数与向量之间的联系很紧密,解题时要时刻注意。
4.解答三角高考题的策略。
(1)发现差异:观察角、函数运算间的差异,即进行所谓的“差异分析”。
(2)寻找联系:运用相关公式,找出差异之间的内在联系。
(3)合理转化:选择恰当的公式,促使差异的转化。
3.证明三角不等式的方法:比较法、配方法、反证法、分析法,利用函数的单调性,利用正、余弦函数的有界性,利用单位圆三角函数线及判别法等。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com