
17.一个口袋内有4个不同的红球,6个不同的白球,
(1)从中任取4个球,红球的个数不比白球少的取法有多少种?
(2)若取一个红球记2分,取一个白球记1分,从中任取5个球,使总分不少于7分的
取法有多少种?
16.安排7位工作人员在5月1日到5月7日值班,每人值班一天,其中甲、乙二人都不能安排在5月1日和2日,不同的安排方法共有_________种。(用数字作答)。
14.在(x4+)10的展开式中常数项是 (用数字作答)。
15设1<m<10且m∈N,若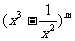 的展开式中存在常数项,则m的值是 ;
的展开式中存在常数项,则m的值是 ;
13.若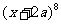 的展开式中含
的展开式中含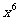 项的系数是448,则正实数
项的系数是448,则正实数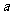 的值为
。
的值为
。
12. 已知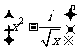 的展开式中第三项与第五项的系数之比为-
的展开式中第三项与第五项的系数之比为-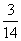 ,其中
,其中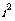 =-1,则展开式中常数项是
=-1,则展开式中常数项是
(A) 45 (B) 45i (C) -45 (D) -45i
11. 某外商计划在5个候选城市投资3个不同的项目,且在同一个城市投资的项目不超过2个,则该外商不同的投资方案有
A.60种 B.70种 C.80种 D.120种
10. 将4个颜色互不相同的球全部放入编号为1和2的两个盒子里,使得放入每个盒子里的球的个数不小于该盒子的编号,则不同的放球方法有
A.10种 B.20种 C.36种 D.52种
8. 8名运动员参加男子100米的决赛. 已知运动场有从内到外编号依次为1,2,3,4,5,6,7,8的八条跑道,若指定的3名运动员所在的跑道编号必须是三个连续数字(如:4,5,6),则参加比赛的这8名运动员安排跑道的方式共有
A.360种 B.4320种 C.720种 D.2160种
9若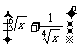 (n∈N+)的展开式中含有常数项,则n必为
(n∈N+)的展开式中含有常数项,则n必为
A.4的倍数 B.5的倍数 C.6的倍数 D.10的倍数
7. 从4台A型笔记本电脑与5台B型笔记本电脑中任选3台,其中至少要有A型和B型笔
记本电脑各一台,则不同的选取方法共有
A.140种 B.84种 C.70种 D.35种
6. 若(1-2x)5的展开式中第二项小于第一项,且不小于第三项,则x的取值范围是
A.x>-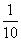 B.x≥-
B.x≥-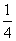 C.-
C.-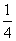 ≤x≤0 D.-
≤x≤0 D.-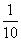 <x≤0
<x≤0
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com