
2、 会根据矩形、菱形、正方形、梯形的性质和判定进行运算和推理,理解顺次连接一个四边形的中点所构造的四边形是特殊的四边形。
1、 能说出矩形、菱形、正方形、梯形的概念和性质,以及四边形是矩形、菱形、正方形、等腰梯形的条件,了解它们之间的关系。知道直角三角形斜边上的中线等于斜边的一半。
4、 运用数形结合的思想、方程的思想解决平行四边形中的计算和证明。
Ⅳ、[实践]
(1) 教师自行设计作业;
(2) 复习指导用书第88--90页第1、4、5、7、8、10、11、13、15、16、17题。
第16课时 特殊平行四边形、梯形与证明
溧阳市第二中学 钱惠琴
复习教学目标:
3、 本节课主要内容:见唤醒中的“知识结构图”。
6、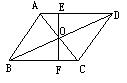 如图,在
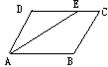
如图,在 ABCD中,EF过对角线的交点O,交AD于E,交BC于F,已知AB=4,BC=5,OE=1.5,则四边形EFCD的周长是
( )
ABCD中,EF过对角线的交点O,交AD于E,交BC于F,已知AB=4,BC=5,OE=1.5,则四边形EFCD的周长是
( )
A、14 B、12 C、16 D、10
Ⅱ、[尝试]
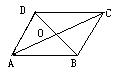
例1: 如图, ABCD的对角线AC,BD相交于点O,由此你能得出哪些结论?试尽可能多的写出一些来.
ABCD的对角线AC,BD相交于点O,由此你能得出哪些结论?试尽可能多的写出一些来.
 分析:分别从平行四边形的边、角、对角线方面去考虑,然后思考从这些结论出发得出的新的结论。
分析:分别从平行四边形的边、角、对角线方面去考虑,然后思考从这些结论出发得出的新的结论。
解:AB=CD ,AD=BC,DO=BO,AO=CO,
∠ADC=∠ABC,∠DAB=∠DCB,∠ADB=∠DBC,∠BDC=∠ABD,∠DCA=∠CAB, ∠ACB=∠DAC
△ADO≌△CBO,△DOC≌△BOA,△ADC≌△CBA,△ADB≌△CBD,
S△DOC=S△AOD=S△AOB=S△BOC 等。
提炼:对于这种结论开放的题目,要注意思维发散,灵活运用平行四边形的性质,从不同的角度去考虑。
例2:图, 已知一个多边形的内角和是它的外角和的5倍,求这个多边形的边数。
分析:注意多边形的外角和始终是360°
解: 设这个多边形是n边形,则
(n-2)×180°=5×360°,得 n=12
答:这个多边形是十二边形。
提炼:多边形的内角和与外角和既有区别,又有联系。多边形的内角和随边数的变化而变化,而外角和是一个定值。已知内角和与外角和的关系,可以运用方程思想解决。
 例3:如图:在
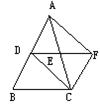
△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE,则图中的平行四边形有哪些?说说你的理由。
例3:如图:在
△ABC中,D、E分别是AB、AC的中点,F是DE延长线上的点,且EF=DE,则图中的平行四边形有哪些?说说你的理由。
分析:已知条件中AE=EC,DE=FE,不难得到四边形ADCF是平行四边形,然后推出AD∥CF,又可证到AD=CF,所以四边形DBCF也是平行四边形。
解: ADCF,
ADCF, DBCF
DBCF
理由:∵D、E分别是AB、AC的中点
∴AE=EC,AD=DB,
又∵EF=DE,∴四边形ADCF是平行四边形(对角线互相平分的四边形是平行四边形)
∴AB∥CF,AD=CF,∴BD=CF,∴四边形DBCF也是平行四边形(一组对边平行且相等的四边形是平行四边形)
提炼:运用数形结合的思想,灵活运用平行四边形的判定方法,关注由结论又可以推出新的结论。
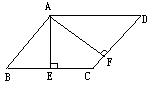
例4:如图,已知 ABCD的周长为40,高AE=6,高AF=9,试根据条件设计一个问题,并进行解答.
ABCD的周长为40,高AE=6,高AF=9,试根据条件设计一个问题,并进行解答.
 分析: 答案不唯一,如:已知
分析: 答案不唯一,如:已知 ABCD的周长和边上的高,会想到平行四边形的面积,而平行四边形的面积要涉及底和高,所以可以设计求平行四边形的边长。
ABCD的周长和边上的高,会想到平行四边形的面积,而平行四边形的面积要涉及底和高,所以可以设计求平行四边形的边长。
解:设计的问题可以是:求AB、BC的长。
因为 ABCD的面积S=BC*AE=CD*AF
ABCD的面积S=BC*AE=CD*AF
所以6BC=9CD,因此BC=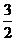 CD,
CD,
又因为 ABCD的周长为40,所以BC+CD=20,可解得AB=8,BC=12
ABCD的周长为40,所以BC+CD=20,可解得AB=8,BC=12
提炼:运用数形结合的思想,将已知条件和图形结合起来考虑。
Ⅲ、[小结]
5、下列图形中,不能进行密铺的是 ( )
A、正三角形 B、正方形 C、正六边形 D、正五边形
4、
如图,在 ABCD中,AE平分∠DAB,∠B=100°,则∠DEA= ( )
ABCD中,AE平分∠DAB,∠B=100°,则∠DEA= ( )
A、100° B、80°
C、60° D、40°
3、若一个多边形的每一个内角都等于120°,则它是 ( )
A、正方形 B、正五边形 C、正六边形 D、正八边形
2、 下列图形是中心对称图形的是 ( )
下列图形是中心对称图形的是 ( )

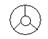 A
B、
C、
D、
A
B、
C、
D、
1、 ABCD的四个内角的度数的比∠A:∠B:∠C:∠D 可能是 ( )
ABCD的四个内角的度数的比∠A:∠B:∠C:∠D 可能是 ( )
A、2:5:2:5 B、3:4:4:3 C、4:4:3:2 D、2:3:5:6
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com