5、如果原命题是假命题,那么它的逆命题一定是假命题.(　 )

4、等腰直角三角形底边上的高等于底边的一半.(　 )

3、等腰三角形中，有一个角是50°，那么它的底角必是65°.(　 )

2、等腰三角形一定不是钝角三角形.(　 )

1、两底角相等的三角形是等腰三角形.(　 )

　　　　　　　　　　　　　　　　 性质:两腰相等、等边对等角、

　　　　　　　　 等腰三角形　　 判定

+ 　　　　　　　　　　　　　　等边三角形　　 性质

特殊三角形　　　　　　　　　　　　　　　　　　　　　　　　　　　 判定

　　　　　　　　　　　　　　　　 性质

　　　　　　　　　 直角三角形　　 判定

含30角的直角三角形的性质：

等腰直角三角形

直角三角形全等的特殊判定方法是：　　　　　　 线段垂直平分线的性质:

3、　 能用分类讨论的思想解决等腰三角形中的有关计算、用转化的思想将不规则图形转化为规则图形.

复习教学过程设计

Ⅰ、[唤醒]

2、　 会用等腰三角形的性质和判定进行有关的计算和证明；会用直角三角形的性质进行简单计算；能写出一个命题的逆命题;会用勾股定理解决简单计算，并会用它的逆定理判定直角三角形；会用“HL”定理判定直角三角形全等。

第14课时　 特殊三角形

溧阳市第二中学　　 彭云

复习教学目标:

1、　 知道等腰三角形和等边三角形的性质和判定；了解直角三角形的概念；知道直角三角形的性质和判定直角三角形的条件;能说出线段中垂线的性质.

例1．已知：直线a∥b，A、B为直线a上两点(点A在B的左边)，C、D为直线b上两点(点C在点D的左边)，AB=CD，画出图形，并连接AD、BC，设交点为O，写出图中所有的全等三角形，并选一对加以证明。

分析：首先按题意画出符合要求的图形，由a‖b、AB=CD得到四边形ABCD为平行四边形，然后根据平行线的性质得到相等的角，再根据三角形全等的条件得到答案。

解略　 (答案：△ABD≌△DCA　 △ABC≌△DCB　 △AOB≌△DOC　 △AOC≌△DOB)

提炼：本题考查平行线的性质及三角形全等的条件，并且涉及读句画图等知识。

例2．例1中，若其他条件不变，把“AB=CD”该为“AC=BD”，则上述所得结论都还一定成立吗？写出仍能成立的，若有不能成立的，画图说明。

分析： 先按题意画出符合要求的图形，并考虑情况的多样性，进一步应用三角形全等的条件。

解略　 (答案：△ABD≌△DCA 、△ABC≌△DCB 、△AOC≌△DOB，其中△AOB≌△DOC不一定成立)

提炼：本题主要说明“SSA”不能说明三角形全等，同时考虑情况的多样性。

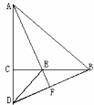
例3．如图，△ABC，△EDC都是等腰直角三角形，且点C在AD上，AE的延长线与BD交于点F，请在图中找出一对全等三角形，并写出证明全等的过程。

分析：由等腰直角三角形的定义可得AC=BC，DC=EC，再由∠ACB=∠DCE可得△ACE≌△BCD

　　　　 证明略

　 提炼：本题考查等腰三角形的定义及三角形全等的条件，也考查学生在复杂问题中寻找所需图形的能力

例4．如图，AB=AE，∠ABC=∠AED，BC=ED，点F是CD的中点。

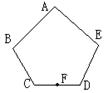(1)求证：AF⊥CD

(2)在你结论证明完毕后，还能得出什么新结论，请写出三个(不要证明)

分析：连接AC、AD，AB=AE，∠ABC=∠ADE　 BC=ED得△ABC≌△AED，得AC=AD ， 又F是CD的中点 ， 所以AF⊥CD。

证明略

提炼：本题考查学生由已知条件构造三角形，用三角形全等的条件得全等三角形，并考查等腰三角形的性质。