
2、 复习指导用书第92--94页练习五、第96--97页练习六。
第17课时 圆(1)
溧阳市第二中学 张云娟
复习教学目标:
1、 教师自行设计作业。
2、 本课运用的数学思想方法:转化思想、类比思想、分类思想等。
Ⅳ、[实践]
1、 单元知识结构(见填空),并重点从边、角、对角线理解特殊平行四边形、梯形的性质和判定。
5、下列各组图形中,既是轴对称图形,又是中心对称图形的是( )
A. 平行四边形、菱形、正方形 B.等腰梯形、矩形、正方形
C.等边三角形、矩形、圆 D.菱形、正方形、圆
Ⅱ. [尝试]
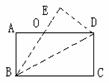 例1、如图,把一张矩形纸片ABCD沿BD对折,使点C落在E处,BE与AD相交于O,写出一组相等的线段______________________________(不包括AB=CD,AD=BC)
例1、如图,把一张矩形纸片ABCD沿BD对折,使点C落在E处,BE与AD相交于O,写出一组相等的线段______________________________(不包括AB=CD,AD=BC)
分析:本题是开放性问题,答案不唯一,可采用两种方法:
(1) 从条件入手,根椐对称性质、全等性质、矩形的性质等,
逐步深入分析,发现需要的结论;
(2) 通过观察、比较找出可能相等的线段,再论证。
解:BE=BC或CD=ED或AB=ED或OB=OD或OA=OE 。
 提炼:折叠的问题实质就是对称的问题,在折叠的问题中折痕所在的直线就是对称轴。在折痕两侧互相重合的部分是全等的图形,从而可以得到许多相等的边、角。
提炼:折叠的问题实质就是对称的问题,在折叠的问题中折痕所在的直线就是对称轴。在折痕两侧互相重合的部分是全等的图形,从而可以得到许多相等的边、角。
例2、
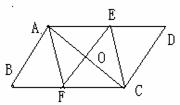
 如图, ABCD的对角线AC的垂直平分线与AD、BC分别交于E、F,
如图, ABCD的对角线AC的垂直平分线与AD、BC分别交于E、F,
求证:四边形AFCE是菱形
分析: 由于四边形AFCE的对角线互相垂直,那么只需证明对角线互相平
分即可,故只需证OE=OF,而这可由证明△AOE≌△COF得到。
证:(略)
提炼:解决此题的关键是要准确理解题意,EF是线段AC的垂直平分线。另一种方法证完后还可问学生,还有其他方法吗?注重一题多解,激活学生的思维。
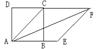
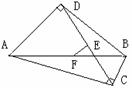 例3、如图,两个四边形中,∠ADB=∠ACB=90º,E、F分别是DC、AB的中点。
例3、如图,两个四边形中,∠ADB=∠ACB=90º,E、F分别是DC、AB的中点。
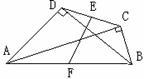
(1) 观察两个图形,你发现了什么?在下面横线上简要写出你的发现
(2) 试猜想EF与DC在位置上有无特殊关系?如有,请证明;如没有,请说明理由。
分析:(1)认真审题,注意图形位置的变化;(2)由直角三角形斜边上的中线等于斜边的一半可知,连结FC、FD,可得FC=1/2AB=FD,又已知CE=DE,根据等腰三角形的三线合一可得EF垂直CD。
略解:(1)图(2)中Rt△ACB由图(1)中Rt△ACB沿AB翻折180º而得到。
(2)EF是CD的中垂线。理由略。
 提炼:要能体会知识之间的内在联系,合理添加辅助线,化难为易。
提炼:要能体会知识之间的内在联系,合理添加辅助线,化难为易。
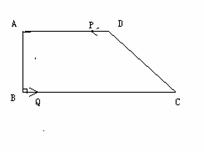
例4、 已知直角梯形ABCD中,AD∥BC,AB⊥BC,AB=6,
AD=8,∠C=45º,有一点P从D向A以每秒1个单位的
速度行动,有一点Q从B向C以每秒1.5个单位的速度
行动。问:在运动过程中四边形PQCD能成为特殊的四边
形吗?什么时候成为怎样特殊的四边形?
分析:由于AD∥BC,四边形PQCD能否成为特殊的四边形,只需看点P、点Q在运动过程中四边形PQCD的对边或邻边能否相等,因此需分情况讨论并计算。
解略(当t= 5.6秒 时,四边形PQCD为平行四边形;当t=0.8秒时,四边形PQCD为等腰梯形;当t=3.2 秒 时,四边形PQCD为直角梯形。)
提炼:要注意数形结合和分类思想,同时考虑问题要全面,防止遗漏。
Ⅲ、[小结]:
4、如图,四边形ABCD是正方形,四边形AEFC是菱形,则∠FAB等于( )
A.45º B.30º C.75º D.22.5º
3、若矩形一内角的平分线分长边为两部分的长分别为2和3,则该矩形的面积为( )
 A.6 B.10 C.15
D.10或15
A.6 B.10 C.15
D.10或15
2、梯形的上底长为6cm,过上底一个顶点引一腰的平行线,交下底所得的三角形的周长是19 cm,那么这个梯形的周长为( )
A.31 cm B.25 cm C.19 cm D.28cm
1、 菱形的一个内角是120º,一边长是8,那么它较短的对角线长是( )
A.3 B.4 C.8
D.8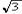
3、 角线互相垂直且相等的四边形是正方形( )
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com