
2、基本数学思想方法:转化的思想;分类讨论的思想;数形结合的思想等。
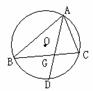 例1、如图,在△ABC中, ∠BAC的平分线AD交△ABC 的外接圆⊙O于点D,交BC于点G,若AG=6,DG=2,求CD的长。
例1、如图,在△ABC中, ∠BAC的平分线AD交△ABC 的外接圆⊙O于点D,交BC于点G,若AG=6,DG=2,求CD的长。
分析:连接DC,用相似三角形解决。
解略。(DC=4)
例2、 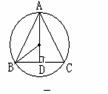 ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径。
ABC中,AB=AC=10,BC=12,求△ABC外接圆的半径。
分析:利用三角形外心的特殊位位置和垂径定理构造直角三角形解决。
解略。( △ABC外接圆的半径为6.25 )。
提炼:善于用数学转化的思想方法,将不同情境下的数学问题转化为比
较熟悉的直角三角形问题解决。
例3、 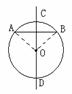 1)如图,小军学完垂径定理,逆向思考得出一个结论:“弦的垂直平分线一定经过圆心,并且平分弦所对的两条弧”,你认为小军的猜测正确吗?为什么?
1)如图,小军学完垂径定理,逆向思考得出一个结论:“弦的垂直平分线一定经过圆心,并且平分弦所对的两条弧”,你认为小军的猜测正确吗?为什么?
(2)你能用上面的结论,帮助考古学家用尺规作图的方法确定古圆盘的半径吗?
分析:(1)根据圆上的点到圆心的距离相等进行说理
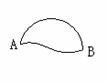 (2)圆心可有两条不同的直径相交确定,因此要确定圆心,只要确
(2)圆心可有两条不同的直径相交确定,因此要确定圆心,只要确
定出两条不同的直径就可,由两条不同的弦,作其垂直平分线,
则 交点就是圆心。
解:(1)∵圆心O到A和B的距离相等,
∴点O一定在AB中垂线上。
即AB的中垂线过圆心。
(2)略
提炼:能将学圆性质时的探究方法灵活运用到探索新的有关结论,并能应用。
例4、 ※如图:把直角三角形ABC的斜边AB放在直线l上,按顺时针方向在l上转动两次,使它转到△A2B2C2的位置,设BC=1,AC=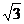 ,则点A运动到点A2的位置时,点A经过的路线长是多少?点A经过的路线与直线l所围成的面积是多少?
,则点A运动到点A2的位置时,点A经过的路线长是多少?点A经过的路线与直线l所围成的面积是多少?
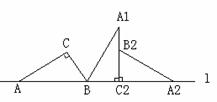 分析:点A经过的路线长就是以B为圆心,以AB
分析:点A经过的路线长就是以B为圆心,以AB
为半径的圆弧和以C2为圆心,以AC为半径的圆
弧的长度。面积就是两个扇形面积与一个直角三角
形的面积和。
解:点A经过的路线长为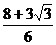 π; 点A经过的路线与直线l所围成的面积是
π; 点A经过的路线与直线l所围成的面积是 π+
π+
提炼:在理解旋转性质的基础上将问题转化为所学的有关圆的计算公式解决。
1.(A)3cm; (B)5cm; (C)6 cm; (D)4 cm
(5)已知△ABC是半径为2的圆内接三角形,若BC=2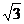 ,则∠A的度数为( )
,则∠A的度数为( )
(A)30°; (B)60°; (C)120°; (D)60°或120°
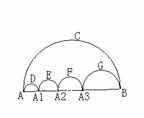 (6)图中的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点甲虫沿弧ADA1、弧A1EA2、弧A2FA3、弧A3GB的路线爬行,乙虫沿弧ACB的路线爬行,则下列结论正确的是( )
(6)图中的五个半圆,邻近的两个半圆相切,两只小虫同时出发,以相同的速度从A点到B点甲虫沿弧ADA1、弧A1EA2、弧A2FA3、弧A3GB的路线爬行,乙虫沿弧ACB的路线爬行,则下列结论正确的是( )
(A)甲虫先到B点; (B)乙虫先到B点;
(C)甲虫、乙虫同时到达B点;(D)无法确定。
1.(A)∏; (B)5∏ ; (C)2∏ ; (D)2.5∏
(4)如果圆锥的侧面展开图的面积是15∏cm 2, 母线长是5cm,那么圆锥的底面半径为( )
3、选择题:
(1)⊙O的直径为10,圆心O到弦AB的中点M的长为3,则弦AB的长是( )
(A)4; (B)6; (C)7; (D)8
(2)△ABC内接于⊙O,AB=AC,∠A=50°,D是⊙O上一点,则∠ADB的度数为( )
(A)50° ; (B)65° ;(C)65°或50° ; (D)115°或65°
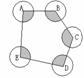 (3)如图所示,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连接五个圆心,得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是( )
(3)如图所示,⊙A、⊙B、⊙C、⊙D、⊙E相互外离,它们的半径都是1,顺次连接五个圆心,得到五边形ABCDE,则图中五个扇形(阴影部分)的面积之和是( )
2、判断:(1)圆是轴对称图形,其对称轴是任意一条直径; ( )
(2)平分弦的直径垂直于弦,并且平分弦所对的弧; ( )
(3)过任意三点可确定一个圆; ( )
(4)任何三角形只有一个外接圆,一个圆也只有一个内接三角形;( )
(5)一条弦所对的圆心角是它所对的圆周角的2倍。 ( )
1、填空

 基本概念: 弧、弦、圆心角、圆周角
基本概念: 弧、弦、圆心角、圆周角
 确定圆的条件:
确定圆的条件:
对称性:
垂径定理及逆定理
圆 基本性质: 圆心角、弧、弦的关系定理:
 圆周角定理:同弧或等弧所对的圆心角是它所对的圆周角的
圆周角定理:同弧或等弧所对的圆心角是它所对的圆周角的
推论:(1)同弧或等弧所的圆周角
(2)90°的圆周角所对弦是 ,
 与圆有关的计算公式 : (1)
;
与圆有关的计算公式 : (1)
;
(2) ;
(3) ;
(4 ) ;
3、 会用折叠、旋转、圆的对称性及分类讨论的思想方法探索图形的有关性质,能将有关弦长、半径的实际计算问题转化成解直角三角形问题解决。
复习过程设计
2、 能用垂径定理,圆心角、弧、弦之间关系定理,圆周角定理及推论,弧长公式等进行简单的运算和推理;会通过作图的方法理解确定圆的条件。
1、 知道圆、弧、弦、圆心角、圆周角等基本概念;认识圆的对称性;了解圆锥的侧面展开图是扇形。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com