
2. 解:(1)在△OAB中,
 ∵
∵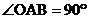 ,
,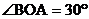 ,∴AB=OB·
,∴AB=OB·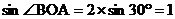
OA= OB·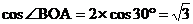
∴点B的坐标为( ,1)
,1)
过点A´作A´D垂直于y轴,垂足为D。
在Rt△OD A´中
|
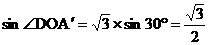 ,
,
OD=OA´·
∴A´点的坐标为(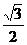 ,
,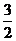 )
)
(2)点B的坐标为( ,1),点B´的坐标为(0,2),设所求的解析式为
,1),点B´的坐标为(0,2),设所求的解析式为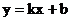 ,则
,则

解得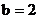 ,
,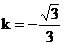 ,∴
,∴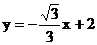
当 时,
时,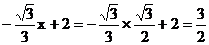
∴A´(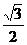 ,
,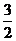 )在直线BB´上。
)在直线BB´上。
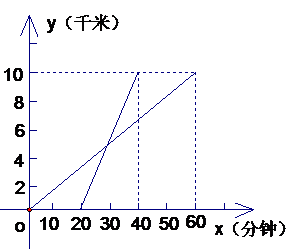
1. 解:(1)长跑: ,骑车:
,骑车: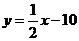 (2)联立以上两个得方程组:
(2)联立以上两个得方程组: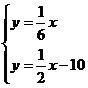
解得:x=30,y=5,即长跑的同学出发了30分钟后,骑自行车的同学就追上了长跑的同学.
5. (-4,3);6. x≥2;7. m<3;8. (4,-4);9. 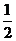 ;10.
;10.  ,
,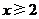 11.
11. 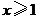
12 .8 13. x≠3;14. 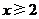 ;15. x≥-且x≠1 16. y=2x;17. 16;18. y=2x+3;19. 大于4;20.
;15. x≥-且x≠1 16. y=2x;17. 16;18. y=2x+3;19. 大于4;20. 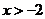 ;21. -3<x<-2;22. -2;23.
;21. -3<x<-2;22. -2;23. 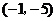 ;24.
;24. 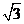 ;25.
;25.  ;26.
;26.
1. 504;2. 3;
3. 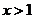 4.
4. 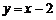 (提示:答案不惟一,如
(提示:答案不惟一,如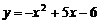 等)
等)
1.A 2.D 3.A 4.C 5. 6.D7.C 8.A 9.A 10.D 11.C 12.C 13.B 14.C 15.A 16. 17.B 18.C 19.A 20.B 21.C 22.C 23.D 24.C 25.A 26.D 27.B 28.D 29.C 30.B 31.B 32.A 33.B 34.D 35.A 36.A
(二)职工个人当年治病花费的医疗费年底按表1的办法分段处理:
表1
|
分段方式 |
处理办法 |
|
不超过150元(含150元) |
全部由个人承担 |
|
超过150元,不超过10000元(不含150元,含10000元)的部分 |
个人承担n%,剩余部分由公司承担 |
|
超过10000元(不含10000元)的部分 |
全部由公司承担 |
设一职工当年治病花费的医疗费为x元,他个人实际承担的费用(包括医疗费个人承担的部分和缴纳的医疗公积金m元)为y元
(1) 由表1可知,当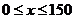 时,
时,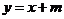 ;那么,当
;那么,当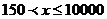 时,y= ;
时,y= ;
(用含m、n、x的方式表示)
(2)该公司职工小陈和大李2007年治病花费的医疗费和他们个人实际承担的费用如表2:
|
职工 |
治病花费的医疗费x(元) |
个人实际承担的费用y(元) |
|
小陈 |
300 |
280 |
|
大李 |
500 |
320 |
请根据表2中的信息,求m、n的值,并求出当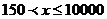 时,y关于x函数解析式;
时,y关于x函数解析式;
(3)该公司职工个人一年因病实际承担费用最多只需要多少元?(直接写出结果)
31.(2008江苏盐城)
在购买某场足球赛门票时,设购买门票数为 (张),总费用为
(张),总费用为 (元).现有两种购买方案:
(元).现有两种购买方案:
方案一:若单位赞助广告费10000元,则该单位所购门票的价格为每张60元;
(总费用=广告赞助费+门票费)
方案二:购买门票方式如图所示.
解答下列问题:
(1)方案一中, 与
与 的函数关系式为
;
的函数关系式为
;
方案二中,当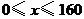 时,
时, 与
与 的函数关系式为
;
的函数关系式为
;
当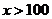 时,
时, 与
与 的函数关系式为
;
的函数关系式为
;
(2)如果购买本场足球赛超过100张,你将选择哪一种方案,使总费用最省?请说明理由;
(3)甲、乙两单位分别采用方案一、方案二购买本场足球赛门票共700张,花去总费用计58000元,求甲、乙两单位各购买门票多少张.
32.(2008四川内江) “5.12”汶川大地震后,某药业生产厂家为支援灾区人民,准备捐赠320箱某种急需药品,该厂家备有多辆甲、乙两种型号的货车,如果单独用甲型号车若干辆,则装满每车后还余20箱未装;如果单独用同样辆数的乙型号车装,则装完后还可以再装30箱,已知装满时,每辆甲型号车比乙型号车少装10箱.
(1)求甲、乙两型号车每辆车装满时,各能装多少箱药品?
(2)已知将这批药品从厂家运到灾区,甲、乙两型号车的运输成本分别为320元/辆和350元/辆.设派出甲型号车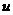 辆,乙型号车
辆,乙型号车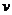 辆时,运输的总成本为
辆时,运输的总成本为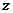 元,请你提出一个派车方案,保证320箱药品装完,且运输总成本
元,请你提出一个派车方案,保证320箱药品装完,且运输总成本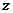 最低,并求出这个最低运输成本为多少元?
最低,并求出这个最低运输成本为多少元?
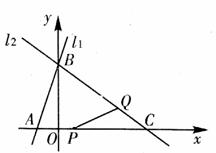
33.(2008山西省)如图,已知直线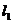 的解析式为
的解析式为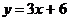 ,直线
,直线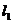 与x轴、y轴分别相交于A、B两点,直线
与x轴、y轴分别相交于A、B两点,直线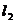 经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线
经过B、C两点,点C的坐标为(8,0),又已知点P在x轴上从点A向点C移动,点Q在直线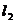 从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(
从点C向点B移动。点P、Q同时出发,且移动的速度都为每秒1个单位长度,设移动时间为t秒(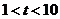 )。
)。
(1)求直线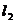 的解析式。
的解析式。
(2)设△PCQ的面积为S,请求出S关于t的函数关系式。
(3)试探究:当t为何值时,△PCQ为等腰三角形?
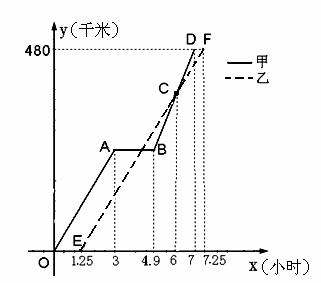
34.(2008泰州市)2008年5月12日14时28分四川汶川发生里氏8.0级强力地震.某市接到上级通知,立即派出甲、乙两个抗震救灾小组乘车沿同一路线赶赴距出发点480千米的灾区.乙组由于要携带一些救灾物资,比甲组迟出发1.25小时(从甲组出发时开始计时).图中的折线、线段分别表示甲、乙两组的所走路程y甲(千米)、y乙(千米)与时间x(小时)之间的函数关系对应的图像.请根据图像所提供的信息,解决下列问题:
(1)由于汽车发生故障,甲组在途中停留了 小时;(2分)
(2)甲组的汽车排除故障后,立即提速赶往灾区.请问甲组的汽车在排除故障时,距出发点的路程是多少千米?(6分)
(3)为了保证及时联络,甲、乙两组在第一次相遇时约定此后两车之间的路程不超过25千米,请通过计算说明,按图像所表示的走法是否符合约定.(4分)
35.(2008贵州贵阳)如图6,反映了甲、乙两名自行车运动员在公路上进行训练时的行驶路程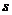 (千米)和行驶时间
(千米)和行驶时间 (小时)之间的关系,根据所给图象,解答下列问题:
(小时)之间的关系,根据所给图象,解答下列问题:
(1)写出甲的行驶路程 和行驶时间
和行驶时间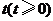 之间的函数关系式.(3分)
之间的函数关系式.(3分)
(2)在哪一段时间内,甲的行驶速度小于乙的行驶速度;在哪一段时间内,甲的行驶速度大于乙的行驶速度.(4分)
(3)从图象中你还能获得什么信息?请写出其中的一条.(3分)
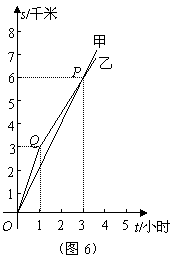

36.(2008年湖南省邵阳市)王师傅开车通过邵怀高速公路雪峰山隧道(全长约为7千米)时,所走路程 (千米)与时间
(千米)与时间 (分钟)之间的函数关系的图象如图(十四)所示.请结合图象,回答下列问题:
(分钟)之间的函数关系的图象如图(十四)所示.请结合图象,回答下列问题:
(1)求王师傅开车通过雪峰山隧道的时间;
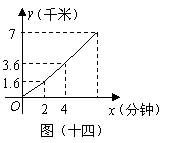 (2)王师傅说:“我开车通过隧道时,有一段连续2分钟恰好走了1.8千米”.你说有可能吗?请说明理由.
(2)王师傅说:“我开车通过隧道时,有一段连续2分钟恰好走了1.8千米”.你说有可能吗?请说明理由.
37.(2008年四川省南充市)某乒乓球训练馆准备购买10副某种品牌的乒乓球拍,每副球拍配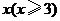 个乒乓球,已知
个乒乓球,已知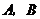 两家超市都有这个品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为20元,每个乒乓球的标价都为1元,现两家超市正在促销,
两家超市都有这个品牌的乒乓球拍和乒乓球出售,且每副球拍的标价都为20元,每个乒乓球的标价都为1元,现两家超市正在促销, 超市所有商品均打九折(按原价的90%付费)销售,而
超市所有商品均打九折(按原价的90%付费)销售,而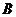 超市买1副乒乓球拍送3个乒乓球,若仅考虑购买球拍和乒乓球的费用,请解答下列问题:
超市买1副乒乓球拍送3个乒乓球,若仅考虑购买球拍和乒乓球的费用,请解答下列问题:
(1)如果只在某一家超市购买所需球拍和乒乓球,那么去 超市还是
超市还是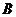 超市买更合算?
超市买更合算?
(2)当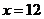 时,请设计最省钱的购买方案.
时,请设计最省钱的购买方案.
38.(2008益阳市)乘坐益阳市某种出租汽车.当行驶 路程小于2千米时,乘车费用都是4元(即起步价4元);当行驶路程大于或等于2千米时,超过2千米部分每千米收费1.5元.
(1)请你求出x≥2时乘车费用y(元)与行驶路程x(千米)之间的函数关系式;
(2)按常规,乘车付费时按计费器上显示的金额进行“四舍五入”后取整(如记费器上的数字显示范围大于或等于9.5而小于10.5时,应付车费10元),小红一次乘车后付了车费8元,请你确定小红这次乘车路程x的范围.
39.(2008宜昌市)为积极响应党中央关于支援5·12汶川地震灾区抗震救灾的号召,宜家工厂日夜连续加班,计划为灾区生产m顶帐篷.生产过程中的剩余生产任务y(顶)与已用生产时间x(时)之间的关系如图所示.
(1)求变量y与x之间的关系式.
(2)求m的值.
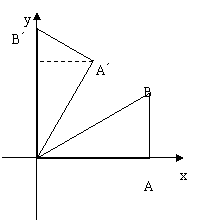
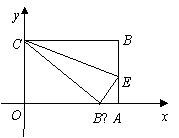
40.(2008年浙江省衢州)如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,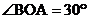
(1)求点B和点A′的坐标;
|
|
|
|
(1)如果按2元/千克的价格销售,能否在60天内售完这些椪柑?按此价格销售,获得的总毛利润是多少元(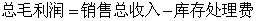 )?
)?
(2)设椪柑销售价格定为x 元/千克时,平均每天能售出y千克,求y关于x的函数解析式;如果要在2月份售完这些椪柑(2月份按28天计算),那么销售价格最高可定为多少元/千克(精确到0.1元/千克)?
元/千克时,平均每天能售出y千克,求y关于x的函数解析式;如果要在2月份售完这些椪柑(2月份按28天计算),那么销售价格最高可定为多少元/千克(精确到0.1元/千克)?
一次函数答案
(一)每位职工在年初需缴纳医疗公积金m元;
1.(2008年四川省宜宾市)
为迎接2008年北京奥运会,某学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威。如图,线段L1,L2分别表示长跑的同学和骑自行车的同学行进的路程y(千米)随时间x(分钟)变化的函数图象。根据图象,解答下列问题:
(1)分别求出长跑的同学和骑自行车的同学的行进路程y与时间x的函数表达式;
(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学?
2.(2008年浙江省衢州市)如图,在平面直角坐标系中,Rt△OAB的直角边OA在x轴的正半轴上,点B在第象限,将△OAB绕点O按逆时针方向旋转至△OA′B′,使点B的对应点B′落在y轴的正半轴上,已知OB=2,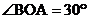
(1)求点B和点A′的坐标;
(2)求经过点B和点B′的直线所对应的一次函数解析式,并判断点A是否在直线BB′上。

3.(2008年浙江省衢州市)1月底,某公司还有11000千克椪柑库存,这些椪柑的销售期最多还有60天,60天后库存的椪柑不能再销售,需要当垃圾处理,处理费为0.05元/吨。经测算,椪柑的销售价格定为2元/千克时,平均每天可售出100千克,销售价格降低,销售量可增加,每降低0.1元/千克,每天可多售出50千克。
(1)如果按2元/千克的价格销售,能否在60天内售完这些椪柑?按此价格销售,获得的总毛利润是多少元(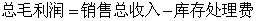 )?
)?
(2)设椪柑销售价格定为x 元/千克时,平均每天能售出y千克,求y关于x的函数解析式;如果要在2月份售完这些椪柑(2月份按28天计算),那么销售价格最高可定为多少元/千克(精确到0.1元/千克)?
元/千克时,平均每天能售出y千克,求y关于x的函数解析式;如果要在2月份售完这些椪柑(2月份按28天计算),那么销售价格最高可定为多少元/千克(精确到0.1元/千克)?
4、(2008年山东省滨州市)已知一次函数的图象过点(1,1)与(2,-1),求这个函数的解析式并求使函数值为正值的x的范围.
5.(2008年山东省临沂市)某商场欲购进A、B两种品牌的饮料500箱,此两种饮料每箱的进价和售价如下表所示。设购进A种饮料x箱,且所购进的两种饮料能全部卖出,获得的总利润为y元。
⑴求y关于x的函数关系式?
⑵如果购进两种饮料的总费用不超过20000元,那么该商场如何进货才能获利最多?并求出最大利润。(注:利润=售价-成本)
|
品牌 |
A |
B |
|
进价(元/箱) |
55 |
35 |
|
售价(元/箱) |
63 |
40 |
6.(2008年浙江省绍兴市)定义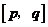 为一次函数
为一次函数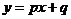 的特征数.
的特征数.
(1)若特征数是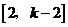 的一次函数为正比例函数,求
的一次函数为正比例函数,求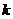 的值;
的值;
(2)设点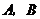 分别为抛物线
分别为抛物线 与
与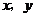 轴的交点,其中
轴的交点,其中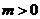 ,且
,且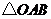 的面积为4,
的面积为4,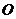 为原点,求图象过
为原点,求图象过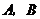 两点的一次函数的特征数.
两点的一次函数的特征数.
7.(2008年沈阳市)一辆经营长途运输的货车在高速公路的 处加满油后,以每小时80千米的速度匀速行驶,前往与
处加满油后,以每小时80千米的速度匀速行驶,前往与 处相距636千米的
处相距636千米的 地,下表记录的是货车一次加满油后油箱内余油量
地,下表记录的是货车一次加满油后油箱内余油量 (升)与行驶时间
(升)与行驶时间 (时)之间的关系:
(时)之间的关系:
行驶时间 (时) (时) |
0 |
1 |
2 |
2.5 |
余油量 (升) (升) |
100 |
80 |
60 |
50 |
(1)请你认真分析上表中所给的数据,用你学过的一次函数、反比例函数和二次函数中的一种来表示 与
与 之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
之间的变化规律,说明选择这种函数的理由,并求出它的函数表达式;(不要求写出自变量的取值范围)
(2)按照(1)中的变化规律,货车从 处出发行驶4.2小时到达
处出发行驶4.2小时到达 处,求此时油箱内余油多少升?
处,求此时油箱内余油多少升?
(3)在(2)的前提下, 处前方18千米的
处前方18千米的 处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在
处有一加油站,根据实际经验此货车在行驶中油箱内至少保证有10升油,如果货车的速度和每小时的耗油量不变,那么在 处至少加多少升油,才能使货车到达
处至少加多少升油,才能使货车到达 地.(货车在
地.(货车在 处加油过程中的时间和路程忽略不计)
处加油过程中的时间和路程忽略不计)
8.(2008年大庆市)甲、乙两个工程队完成某项工程,假设甲、乙两个工程队的工作效率是一定的,工程总量为单位1.甲队单独做了10天后,乙队加入合作完成剩下的全部工程,工程进度如图所示.
(1)甲队单独完成这项工程,需 天.
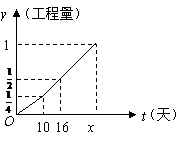 (2)求乙队单独完成这项工程所需的天数.
(2)求乙队单独完成这项工程所需的天数.
(3)求出图中 的值.
的值.
9..(2008年陕西省)
|
 两种树的混合体,需要购买这两种树苗2000棵.种植
两种树的混合体,需要购买这两种树苗2000棵.种植 两种树苗的相关信息如下表:
两种树苗的相关信息如下表:

|
单价(元/棵) |
成活率 |
劳务费(元/棵) |
||
|
A |
15 |
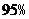 |
3 |
||
|
B |
20 |
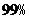 |
4 |
设购买 种树苗
种树苗 棵,造这片林的总费用为
棵,造这片林的总费用为 元.解答下列问题:
元.解答下列问题:
(1)写出 (元)与
(元)与 (棵)之间的函数关系式;
(棵)之间的函数关系式;
(2)假设这批树苗种植后成活1960棵,则造这片林的总费用需多少元?
10.(2008年江苏省连云港市)如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的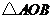 ,
,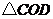 处,直角边
处,直角边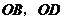 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至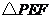 处时,设
处时,设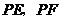 与
与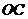 分别交于点
分别交于点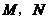 ,与
,与 轴分别交于点
轴分别交于点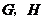 .
.
(1)求直线 所对应的函数关系式;
所对应的函数关系式;
(2)当点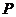 是线段
是线段 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点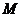 到
到 轴的距离
轴的距离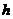 与线段
与线段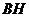 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积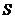 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及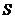 取最大值时点
取最大值时点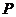 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.


11.(2008北京)如图,已知直线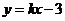 经过点
经过点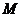 ,求此直线与
,求此直线与 轴,
轴, 轴的交点坐标.
轴的交点坐标.
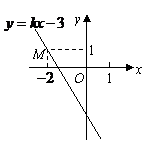

12.(2008湖北咸宁)如图,在平面直角坐标系中,直线l是第一、三象限的角平分线.
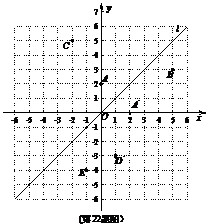 实验与探究:
实验与探究:
(1)
由图观察易知A(0,2)关于直线l的对称点 的坐标为(2,0),请在图中分别标明
的坐标为(2,0),请在图中分别标明
B(5,3) 、C(-2,5) 关于直线l的对称点 、
、 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: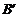 、
、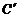 ;
;
归纳与发现:
(2)
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点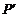 的坐标为
(不必证明);
的坐标为
(不必证明);
运用与拓广:
(3) 已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
13.(2008年云南省双柏县)依法纳税是每个公民应尽的义务.从2008年3月1日起,新修改后的《中华人民共和国个人所得税法》规定,公民每月收入不超过2000元,不需交税;超过2000元的部分为全月应纳税所得额,都应纳税,且根据超过部分的多少按不同的税率纳税,详细的税率如下表:
|
级别 |
全月应纳税所得额 |
税率(%) |
|
1 |
不超过500元的 |
5 |
|
2 |
超过500元至2 000元的部分 |
10 |
|
3 |
超过2 000元至5 000元的部分 |
15 |
|
4 |
超过5 000元至20 000元的部分 |
20 |
|
… |
… |
… |
(1)某工厂一名工人2008年3月的收入为2 400元,问他应交税款多少元?
(2)设x表示公民每月收入(单位:元),y表示应交税款(单位:元),
当2500≤x≤4000时,请写出y关于x的函数关系式;
(3)某公司一名职员2008年4月应交税款120元,问该月他的收入是多少元?
14..(2008年山东省枣庄市)如图,在直角坐标系中放入一个边长OC为9的矩形纸片ABCO.将纸片翻折后,点B恰好落在x轴上,记为B′,折痕为CE,已知tan∠OB′C=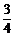 .
.
 (1)求B′ 点的坐标;
(1)求B′ 点的坐标;
(2)求折痕CE所在直线的解析式.
15.(2008山东济南)已知:如图,直线y=- x+4
x+4 与x轴相交于点A,与直线y=
与x轴相交于点A,与直线y= x相交于点P.
x相交于点P.
(1)求点P的坐标.
(2)请判断△OPA的形状并说明理由.

 (3)动点E从原点O出发,以每秒1个单位的速度沿着O P A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B,设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
(3)动点E从原点O出发,以每秒1个单位的速度沿着O P A的路线向点A匀速运动(E不与点O、A重合),过点E分别作EF⊥x轴于F,EB⊥y轴于B,设运动t秒时,矩形EBOF与△OPA重叠部分的面积为S.
求:①S与t之间的函数关系式.
②当t为何值时,S最大,并求出S的最大值.

16.(2008
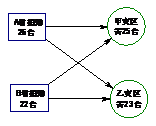
湖北 十堰)5月12日,我国四川省汶川县等地发生强烈地震,在抗震救灾中得知,甲、乙两个重灾区急需一种大型挖掘机,甲地需要25台,乙地需要23台;A、B两省获知情况后慷慨相助,分别捐赠该型号挖掘机26台和22台并将其全部调往灾区.如果从A省调运一台挖掘机到甲地要耗资0.4万元,到乙地要耗资0.3万元;从B省调运一台挖掘机到甲地要耗资0.5万元,到乙地要耗资0.2万元.设从A省调往甲地 台挖掘机,A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元.
台挖掘机,A、B两省将捐赠的挖掘机全部调往灾区共耗资y万元.
⑴请直接写出y与x之间的函数关系式及自变量x的取值范围;
⑵若要使总耗资不超过15万元,有哪几种调运方案?
⑶怎样设计调运方案能使总耗资最少?最少耗资是多少万元?
17. (2008 湖南 益阳)乘坐益阳市某种出租汽车.当行驶 路程小于2千米时,乘车费用都是4元(即起步价4元);当行驶路程大于或等于2千米时,超过2千米部分每千米收费1.5元.
(1)请你求出x≥2时乘车费用y(元)与行驶路程x(千米)之间的函数关系式;
(2)按常规,乘车付费时按计费器上显示的金额进行“四舍五入”后取整(如记费器上的数字显示范围大于或等于9.5而小于10.5时,应付车费10元),小红一次乘车后付了车费8元,请你确定小红这次乘车路程x的范围.
18.(2008 四川 广安) “5.12”汶川特大地震灾害发生后,社会各界积极为灾区捐款捐物,某经销商在当月销售的甲种啤酒尚有2万元货款未收到的情况下,先将销售甲种啤酒全部应收货款的70%捐给了灾区,后又将该月销售乙种啤酒所得的全部货款的80%捐给了灾区.已知该月销售甲、乙两种啤酒共5000件,甲种啤酒每件售价为50元,乙种啤酒每件售价为35元,设该月销售甲种啤酒 件,共捐助救灾款
件,共捐助救灾款 元.
元.
(1)该经销商先捐款
元,后捐款
元.(用含 的式子表示)
的式子表示)
(2)写出 与
与 的函数关系式,并求出自变量
的函数关系式,并求出自变量 的取值范围.
的取值范围.
(3)该经销商两次至少共捐助多少元?
19.(2008 湖南
长沙)在平面直角坐标系中,一动点P(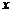 ,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间
,y)从M(1,0)出发,沿由A(-1,1),B(-1,-1),C(1,-1),D(1,1)四点组成的正方形边线(如图①)按一定方向运动。图②是P点运动的路程s(个单位)与运动时间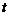 (秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.
(秒)之间的函数图象,图③是P点的纵坐标y与P点运动的路程s之间的函数图象的一部分.


(图①) (图②) (图③)
20.(2008 四川 广安) “5.12”汶川地震发生后,某天广安先后有两批自愿者救援队分别乘客车和出租车沿相同路线从广安赶往重灾区平武救援,下图表示其行驶过程中路程随时间的变化图象.
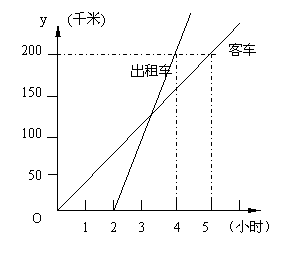 (1)根据图象,请分别写出客车和出租车行驶过程中路程与时间之间的函数关系式(不写出自变量的取值范围);
(1)根据图象,请分别写出客车和出租车行驶过程中路程与时间之间的函数关系式(不写出自变量的取值范围);
(2)写出客车和出租车行驶的速度分别是多少?
(3)试求出出租车出发后多长时间赶上客车?
21.(2008 重庆)为支持四川抗震救灾,重庆市A、B、C三地现在分别有赈灾物资100吨,、100吨、80吨,需要全部运往四川重灾地区的D、E两县。根据灾区的情况,这批赈灾物资运往D县的数量比运往E县的数量的2倍少20吨。
(1)求这批赈灾物资运往D、E两县的数量各是多少?
(2)若要求C地运往D县的赈灾物资为60吨,A地运往D的赈灾物资为x吨(x为整数),B地运往D县的赈灾物资数量小于A地运往D县的赈灾物资数量的2倍。其余的赈灾物资全部运往E县,且B地运往E县的赈灾物资数量不超过25吨。则A、B两地的赈灾物资运往D、E两县的方案有几种?请你写出具体的运送方案;
(3)已知A、B、C三地的赈灾物资运往D、E两县的费用如下表:
|
|
A地 |
B地 |
C地 |
|
运往D县的费用(元/吨) |
220 |
200 |
200 |
|
运往E县的费用(元/吨) |
250 |
220 |
210 |
为即使将这批赈灾物资运往D、E两县,某公司主动承担运送这批赈灾物资的总费用,在(2)问的要求下,该公司承担运送这批赈灾物资的总费用最多是多少?
22.(2008
河北)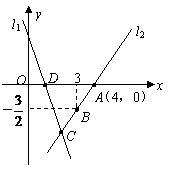 如图,直线
如图,直线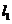 的解析表达式为
的解析表达式为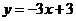 ,且
,且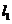 与
与 轴交于点
轴交于点 ,直线
,直线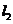 经过点
经过点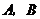 ,直线
,直线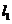 ,
,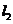 交于点
交于点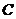 .
.
(1)求点 的坐标;
的坐标;
(2)求直线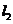 的解析表达式;
的解析表达式;
(3)求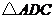 的面积;
的面积;
(4)在直线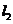 上存在异于点
上存在异于点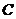 的另一点
的另一点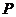 ,使得
,使得
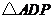 与
与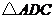 的面积相等,请直接写出点
的面积相等,请直接写出点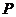 的坐标.
的坐标.
23.(2008 江西)如图,点 的坐标分别为(0,1),(
的坐标分别为(0,1),(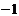 ,0),(1,0),设点
,0),(1,0),设点 与
与 三点构成平行四边形.
三点构成平行四边形.
(1)写出所有符合条件的点 的坐标;
的坐标;
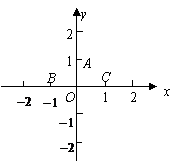 (2)选择(1)中的一点
(2)选择(1)中的一点 ,求直线
,求直线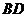 的解析式.
的解析式.
24.(08乌兰察布市)声音在空气中传播的速度 (m/s)是气温
(m/s)是气温 (℃)的一次函数,下表列出了一组不同气温的音速:
(℃)的一次函数,下表列出了一组不同气温的音速:
气温 (℃) (℃) |
0 |
5 |
10 |
15 |
20 |
音速 (m/s) (m/s) |
331 |
334 |
337 |
340 |
343 |
(1)求 与
与 之间的函数关系式;
之间的函数关系式;
(2)气温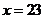 ℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
℃时,某人看到烟花燃放5s后才听到声响,那么此人与烟花燃放地约相距多远?
25.(2008泰安)某厂工人小王某月工作的部分信息如下:
信息一:工作时间:每天上午8∶00~12∶00,下午14∶00~18∶00,每月25天;
信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.
生产产品件数与所用时间之间的关系见下表:
|
生产甲产品件数(件) |
生产乙产品件数(件) |
所用总时间(分) |
|
10 |
10 |
350 |
|
30 |
20 |
850 |
信息三:按件计酬,每生产一件甲产品可得1.50元,每生产一件乙产品可得2.80元.
根据以上信息,回答下列问题:
(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分?
(2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?
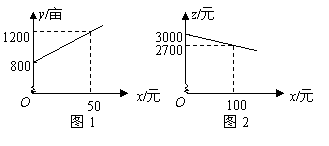
26.(2008泰安)某市种植某种绿色蔬菜,全部用来出口.为了扩大出口规模,该市决定对这种蔬菜的种植实行政府补贴,规定每种植一亩这种蔬菜一次性补贴菜农若干元.经调查,种植亩数 (亩)与补贴数额
(亩)与补贴数额 (元)之间大致满足如图1所示的一次函数关系.随着补贴数额
(元)之间大致满足如图1所示的一次函数关系.随着补贴数额 的不断增大,出口量也不断增加,但每亩蔬菜的收益
的不断增大,出口量也不断增加,但每亩蔬菜的收益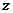 (元)会相应降低,且
(元)会相应降低,且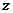 与
与 之间也大致满足如图2所示的一次函数关系.
之间也大致满足如图2所示的一次函数关系.
(1)在政府未出台补贴措施前,该市种植这种蔬菜的总收益额为多少?
(2)分别求出政府补贴政策实施后,种植亩数 和每亩蔬菜的收益
和每亩蔬菜的收益 与政府补贴数额
与政府补贴数额 之间的函数关系式;
之间的函数关系式;
(3)要使全市这种蔬菜的总收益 (元)最大,政府应将每亩补贴数额
(元)最大,政府应将每亩补贴数额 定为多少?并求出总收益
定为多少?并求出总收益 的最大值.
的最大值.

27.(2008广东)已知直线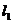 :
: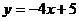 和直线
和直线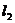 ::
::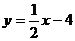 ,求两条直线
,求两条直线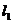 和
和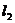 的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.
的交点坐标,并判断该交点落在平面直角坐标系的哪一个象限上.
28、(2008湖北武汉)
⑴点(0,1)向下平移2个单位后的坐标是
,直线 向下平移2个单位后的解析式是
;
向下平移2个单位后的解析式是
;
⑵直线 向右平移2个单位后的解析式是
;
向右平移2个单位后的解析式是
;
⑶如图,已知点C为直线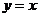 上在第一象限内一点,直线
上在第一象限内一点,直线 交
交 轴于点A,交
轴于点A,交 轴于B,将直线AB沿射线OC方向平移
轴于B,将直线AB沿射线OC方向平移 个单位,求平移后的直线的解析式.
个单位,求平移后的直线的解析式.


29.(2008湖北襄樊)我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费办法收费.即一月用水10吨以内(包括10吨)用户,每吨收水费a元;一月用水超过10吨的用户,10吨水仍按每吨a元水费,超过的部分每吨按b元(b>a)收费.设一户居民月用水y元,y与x之间的函数关系如图所示.
(1) 求a的值,若某户居民上月用水8吨,应收水费多少元?
(2) 求b的值,并写出当x大于10时,y与x之间的函数关系;
(3) 已知居民甲上月比居民乙多用水4吨,两家共收水费46
元,求他们上月分别用水多少吨?

30.(2008湖北孝感)某股份有限公司根据公司实际情况,对本公司职工实行内部医疗公积金制度,公司规定:
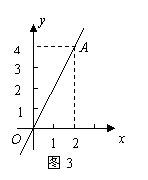
25.(2008年上海市)在图3中,将直线 向上平移1个单位,得到一个一次函数的图像,那么这个一次函数的解析式是
.
向上平移1个单位,得到一个一次函数的图像,那么这个一次函数的解析式是
.

24.(2008年上海市)已知函数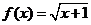 ,那么
,那么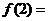 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com