
22. 解:(1)由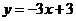 ,令
,令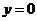 ,得
,得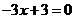 .
.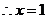 .
. .
.
(2)设直线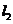 的解析表达式为
的解析表达式为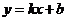 ,由图象知:
,由图象知: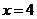 ,
,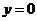 ;
;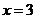 ,
,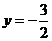 .
.
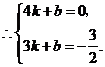
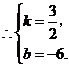
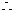 直线
直线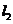 的解析表达式为
的解析表达式为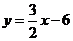 .
.
(3)由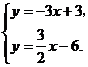 解得
解得
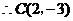 .
.
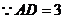 ,
,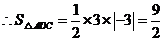 .
.
(4)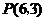 .
.
21. 解:(1)设这批赈灾物资运往 县的数量为
县的数量为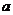 吨,运往
吨,运往 县的数量为
县的数量为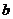 吨.
吨.
由题意,得
解得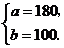
答:这批赈灾物资运往 县的数量为180吨,运往
县的数量为180吨,运往 县的数量为100吨.
县的数量为100吨.
(2)由题意,得
解得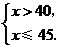 即
即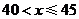 .
.
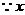 为整数,
为整数, 的取值为41,42,43,44,45.
的取值为41,42,43,44,45.
则这批赈灾物资的运送方案有五种.
具体的运送方案是:
方案一: 地的赈灾物资运往
地的赈灾物资运往 县41吨,运往
县41吨,运往 县59吨;
县59吨;
 地的赈灾物资运往
地的赈灾物资运往 县79吨,运往
县79吨,运往 县21吨.
县21吨.
方案二: 地的赈灾物资运往
地的赈灾物资运往 县42吨,运往
县42吨,运往 县58吨;
县58吨;
 地的赈灾物资运往
地的赈灾物资运往 县78吨,运往
县78吨,运往 县22吨.
县22吨.
方案三: 地的赈灾物资运往
地的赈灾物资运往 县43吨,运往
县43吨,运往 县57吨;
县57吨;
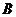 地的赈灾物资运往
地的赈灾物资运往 县77吨,运往
县77吨,运往 县23吨.
县23吨.
方案四: 地的赈灾物资运往
地的赈灾物资运往 县44吨,运往
县44吨,运往 县56吨;
县56吨;
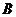 地的赈灾物资运往
地的赈灾物资运往 县76吨,运往
县76吨,运往 县24吨.
县24吨.
方案五: 地的赈灾物资运往
地的赈灾物资运往 县45吨,运往
县45吨,运往 县55吨;
县55吨;
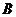 地的赈灾物资运往
地的赈灾物资运往 县75吨,运往
县75吨,运往 县25吨.
县25吨.
(3)设运送这批赈灾物资的总费用为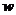 元.由题意,得
元.由题意,得
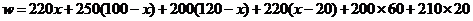
 .
.
因为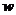 随
随 的增大而减小,且
的增大而减小,且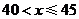 ,
, 为整数.
为整数.
所以,当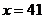 时,
时,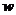 有最大值.则该公司承担运送这批赈灾物资的总费用最多为:
有最大值.则该公司承担运送这批赈灾物资的总费用最多为:
 (元).
(元).
20. 解:(1)客车行驶过程中路程与时间的函数关系式为y=40x
出租车行驶过程中路程与时间的函数关系式为y=100(x-2)
(2)客车行驶的速度为40千米/时
出租车行驶的速度为100千米/时
(3)由题意得 40x=100x-200
解得x=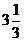
∴x-2=
答:当出租车出发 小时赶上客车。
小时赶上客车。
19. 解:(1)s与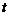 之间的函数关系式是:
;
之间的函数关系式是:
;
(2)与图③相对应的P点的运动路径是: ;P点出发 秒首次到达点B;
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
解:(1)S= (t≥0)(2分)
(t≥0)(2分)
(2)M→D→A→N, 10
(3)当3≤s<5,即P从A到B时,y=4-s;
当5≤s<7,即P从B到C时,y=-1;
当7≤s≤8,即P从C到M时,y=s-8.
补全图象略.
18. 解:(1)50x·70%或35x 35(5000-x)·80%或(140000-28x)
(2)y与x的函数关系式是:y=7x+140000
由题意得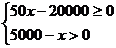 解得400≤x≤500
解得400≤x≤500
∴自变量x的取值范围是400≤x≤500
(3)∵y=7x+140000是一个一次函数
且7>0 ,400≤x≤500
∴当x=400时,y的最小值为142800
答:该经销商两次至少共捐款142800元
17. (1) 根据题意可知:y=4+1.5(x-2) ,
∴ y=1.5x+1(x≥2)
(2)依题意得:7.5≤1.5x+1<8.5
∴ 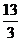 ≤x<5
≤x<5
16. 解:⑴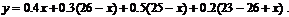
或:
即: (
( )
)
⑵依题意,得
解之,得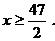
又∵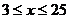 ,且x为整数, ∴
,且x为整数, ∴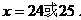
即,要使总耗资不超过15万元,有如下两种调运方案:
方案一:从A省往甲地调运24台,往乙地调运2台;从B省往甲地
调运1台,往乙地调运21台.
方案二:从A省往甲地调运25台,往乙地调运1台;从B省往甲地
调运0台,往乙地调运22台.
⑶由⑴知: (
(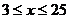 )
)
∵-0.2<0, ∴ 随
随 的增大而减小.
的增大而减小.
∴当 时,∴
时,∴
答:设计如下调运方案:从A省往甲地调运25台,往乙地调运1台;
从B省往甲地调运0台,往乙地调运22台,能使总耗资最少,
最少耗资为14.7万元.
15. 解:(1)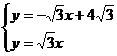 ……1分
……1分
解得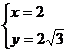 ……2分
……2分
所以点P的坐标为(2,2 )
)
(2)将y=0代入y=- x+4
x+4 ,-
,- x+4
x+4 =0,所以x=4,即OA=4……4分
=0,所以x=4,即OA=4……4分
作PD⊥OA于D,则OD=2,PD=2 ,
,
∵tan∠POA= =
= ,∴∠POA=60°……5分
,∴∠POA=60°……5分
∵OP= =4
=4
∴△POA是等边三角形.……6分
(3)①当0<t≤4时,如图1,
在Rt△EOF中,∵∠EOF=60°,OE=t,
∴EF= ,OF=
,OF=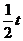 ,∴S=
,∴S= ·OF·EF=
·OF·EF= ……7分
……7分
|
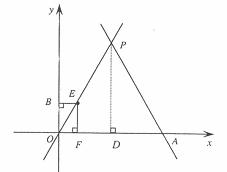
当4<t<8时,如图2,设EB与OP相交于点C,易知:CE=PE=t-4,AE=8-t,
 ∴AF=4-
∴AF=4-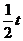 ,EF=
,EF=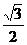 (8-t),∴OF=OA-AF=4-(4-
(8-t),∴OF=OA-AF=4-(4-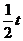 )=
)=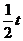 ,
,
∴S= (CE+OF)·EF=
(CE+OF)·EF= (t-4+
(t-4+ t)×
t)×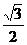 (8-t)
(8-t)
=-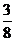
 t2+4
t2+4 t-8
t-8 ……8分
……8分
②当0<t≤4时,S= ,t=4时,S最大=2
,t=4时,S最大=2 .
.
当4<t<8时,S=-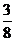
 t2+4
t2+4 t-8
t-8 =-
=-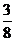
 (t-
(t-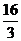 )2+
)2+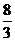

t=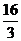 时,S最大=
时,S最大=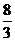
 ……9分
……9分
14. 解:(1)在Rt△B′OC中,tan∠OB′C=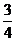 ,OC=9,
,OC=9,
∴ 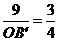 . ………………………………………………………………………2分
. ………………………………………………………………………2分
解得OB′=12,即点B′ 的坐标为(12,0). ………………………………………3分
(2)将纸片翻折后,点B恰好落在x轴上的B′ 点,CE为折痕,
∴ △CBE≌△CB′E,故BE=B′E,CB′=CB=OA.
由勾股定理,得 CB′=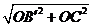 =15. … …………………………………4分
=15. … …………………………………4分
设AE=a,则EB′=EB=9-a,AB′=AO-OB′=15-12=3.
由勾股定理,得 a2+32=(9-a)2,解得a=4.
∴点E的坐标为(15,4),点C的坐标为(0,9). ································ 5分
设直线CE的解析式为y=kx+b,根据题意,得 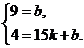 …………… 6分
…………… 6分
解得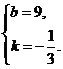 ∴CE所在直线的解析式为 y=-
∴CE所在直线的解析式为 y=-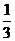 x+9. …………………8分
x+9. …………………8分
13. 解:(1)该工人3月的收入2 400元中,应纳税的部分是400元,按纳税的税率表,
他应交纳税款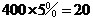 (元);
(元);
(2)当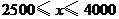 时,其中2 000元不用纳税,应纳税的部分在500元至2 000元之间,其中500元按
时,其中2 000元不用纳税,应纳税的部分在500元至2 000元之间,其中500元按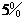 交纳,剩余部分按
交纳,剩余部分按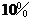 交纳,
交纳,
于是,有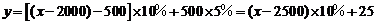 ;
;
即 关于
关于 的函数关系式为
的函数关系式为 .
.
(3)根据(2)可知,当收入为2 500元至4 000元之间时,纳税额在25元至175元之间,于是,由该职员纳税款120元,可知他的收入肯定在2 500元至4 000元之间;
设他的收入为z元,由(2)可得: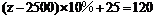 ,解得:z=3450;
,解得:z=3450;
故该职员2008年4月的收入为3450元.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com