
5. __________ __________ __________(骑自行车) to work is good for our health, I think.
4. His father often goes to work __________ __________ (乘公共汽车).
3. Li Lei __________ (乘) the subway to school every day.
2. My grandma goes to the park __________ __________ (步行)every morning.
1. The girl __________ (花费) a lot of time collecting toys last year.
12.(2008·湖北理,16)已知函数f(t)=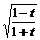 ,g(x)=cosx·f(sinx)+sinx·f(cosx),x∈
,g(x)=cosx·f(sinx)+sinx·f(cosx),x∈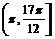 .
.
(1)将函数g(x)化简成Asin(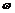 x+
x+ )+B(A>0,
)+B(A>0, 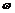 >0,
>0, 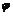 ∈[0,2
∈[0,2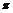 ))的形式;
))的形式;
(2)求函数g(x)的值域.
解 (1)g(x)=cosx·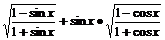
=cosx·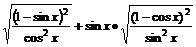
=cosx·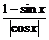 +sinx·
+sinx·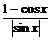 .
.
∵x∈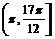 ,∴|cosx|=-cosx,|sinx|=-sinx.
,∴|cosx|=-cosx,|sinx|=-sinx.
∴g(x)=cosx·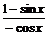 +sinx·
+sinx·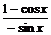
=sinx+cosx-2=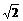 sin
sin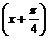 -2.
-2.
(2)由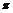 <x≤
<x≤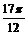 ,得
,得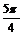 <x+
<x+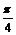 ≤
≤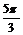 .
.
∵sint在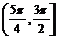 上为减函数,在
上为减函数,在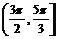 上为增函数,
上为增函数,
sin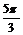 <sin
<sin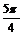 ,
,
∴sin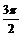 ≤sin
≤sin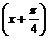 <sin
<sin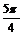
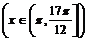
即-1≤sin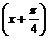 <-
<-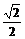 ,
,
∴-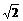 -2≤
-2≤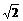 sin
sin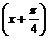 -2<-3,
-2<-3,
故g(x)的值域为[-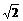 -2,-3).
-2,-3).
11.(2008·安徽理,17)已知函数f(x)=cos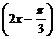 +2sin
+2sin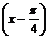 ·sin
·sin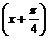 .
.
(1)求函数f(x)的最小正周期和图象的对称轴方程;
(2)求函数f(x)在区间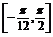 上的值域.
上的值域.
解 (1)∵f(x)=cos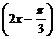 +2sin
+2sin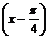 ·sin
·sin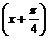
=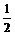 cos2x+
cos2x+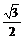 sin2x+(sinx-cosx)(sinx+cosx)
sin2x+(sinx-cosx)(sinx+cosx)
=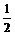 cos2x+
cos2x+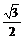 sin2x+sin2x-cos2x
sin2x+sin2x-cos2x
=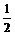 cos2x+
cos2x+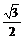 sin2x-cos2x=sin
sin2x-cos2x=sin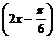 .
.
∴周期T=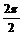 =
=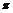 .
.
由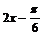 =k
=k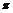 +
+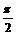 (k∈Z),得x=
(k∈Z),得x=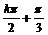 (k∈Z).
(k∈Z).
∴函数图象的对称轴方程为x=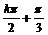 (k∈Z).
(k∈Z).
(2)∵x∈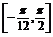 ,∴
,∴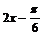 ∈
∈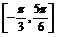 .
.
∵f(x)=sin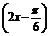 在区间
在区间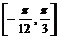 上单调递增,在区间
上单调递增,在区间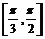 上单调递减,
上单调递减,
∴当x=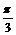 时,f(x)取得最大值1,
时,f(x)取得最大值1,
又∵f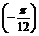 =-
=-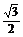 <f
<f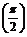 =
=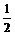 ,
,
∴当x=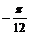 时,f(x)取得最小值-
时,f(x)取得最小值-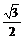 .
.
∴函数f(x)在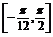 上的值域为
上的值域为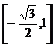 .
.
10.已知函数f(x)=sin(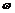 x+
x+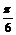 )+sin(
)+sin(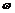 x-
x-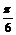 )-2cos2
)-2cos2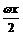 ,x∈R(其中
,x∈R(其中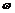 >0).
>0).
(1)求函数f(x)的值域;
(2)若对任意的a∈R,函数y=f(x),x∈(a,a+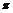 ]的图象与直线y=-1有且仅有两个不同的交点,试确定
]的图象与直线y=-1有且仅有两个不同的交点,试确定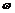 的值(不必证明),并求函数y=f(x),x∈R的单调增区间.
的值(不必证明),并求函数y=f(x),x∈R的单调增区间.
解 (1)f(x)=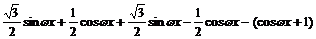
=2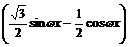 -1
-1
=2sin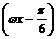 -1.
-1.
由-1≤sin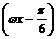 ≤1,得-3≤2sin
≤1,得-3≤2sin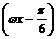 -1≤1.
-1≤1.
可知函数f(x)的值域为[-3,1].
(2)由题设条件及三角函数图象和性质可知,y=f(x)的周期为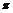 ,又由
,又由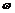 >0,得
>0,得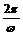 =
=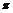 ,即得
,即得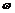 =2.
=2.
于是有f(x)=2sin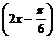 -1,
-1,
再由2k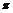 -
-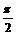 ≤2x-
≤2x-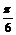 ≤2k
≤2k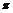 +
+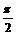 (k∈Z),
(k∈Z),
解得k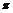 -
-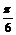 ≤x≤k
≤x≤k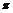 +
+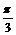 (k∈Z).
(k∈Z).
所以y=f(x)的单调增区间为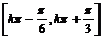 (k∈Z).
(k∈Z).
9.是否存在实数a,使得函数y=sin2x+acosx+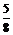 a-
a-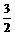 在闭区间
在闭区间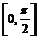 上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
上的最大值是1?若存在,求出对应的a值;若不存在,说明理由.
解 y=1-cos2x+acosx+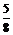 a-
a-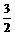
=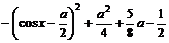
当0≤x≤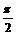 时,0≤cosx≤1,
时,0≤cosx≤1,
若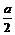 >1,即a>2,则当cosx=1时
>1,即a>2,则当cosx=1时
ymax=a+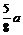 -
-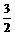 =1,∴a=
=1,∴a=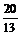 <2(舍去).
<2(舍去).
若0≤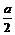 ≤1,即0≤a≤2,则当cosx=
≤1,即0≤a≤2,则当cosx=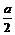 时,
时,
ymax=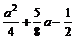 =1,∴a=
=1,∴a=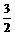 或a=-4(舍去).
或a=-4(舍去).
若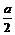 <0,即a<0时,则当cosx=0时,
<0,即a<0时,则当cosx=0时,
ymax=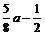 =1,∴a=
=1,∴a=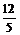 >0(舍去).
>0(舍去).
综上所述,存在a=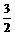 符合题设.
符合题设.
8.函数y=|sinx|cosx-1的最小正周期与最大值的和为 .
答案 2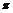 -
-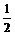
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com