12．双曲线的准线方程：

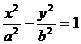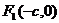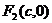对于来说，相对于左焦点对应着左准线，相对于右焦点对应着右准线；

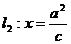焦点到准线的距离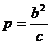(也叫焦参数).

对于来说，相对于上焦点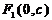对应着上准线；相对于下焦点对应着下准线

抛物线

图形
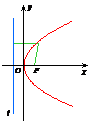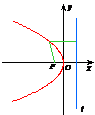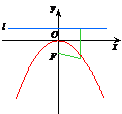方程
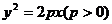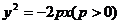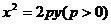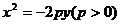焦点
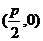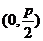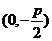准线

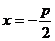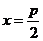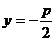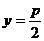11． 双曲线的第二定义：到定点F的距离与到定直线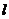的距离之比为常数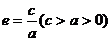的点的轨迹是双曲线.　 其中，定点叫做双曲线的焦点，定直线叫做双曲线的准线.　 常数e是双曲线的离心率．

10．双曲线的几何性质：

(1)范围、对称性　

由标准方程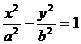，从横的方向来看，直线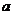x=-,x=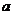之间没有图象，从纵的方向来看，随着x的增大，y的绝对值也无限增大，所以曲线在纵方向上可无限伸展，不像椭圆那样是封闭曲线. 双曲线不封闭，但仍称其对称中心为双曲线的中心.

(2)顶点

顶点：，特殊点：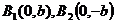

实轴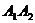：长为2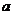,　 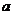叫做半实轴长. 虚轴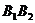：长为2b，b叫做虚半轴长.

双曲线只有两个顶点，而椭圆则有四个顶点，这是两者的又一差异.

(3)渐近线

过双曲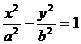线的渐近线() .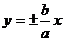

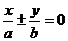(4)离心率

双曲线的焦距与实轴长的比，叫做双曲线的离心率. 范围：

双曲线形状与e的关系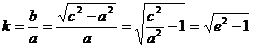：，e越大，即渐近线的斜率的绝对值就大，这时双曲线的形状就从扁狭逐渐变得开阔. 由此可知，双曲线的离心率越大，它的开口就越阔.　

9.焦点的位置:从椭圆的标准方程不难看出椭圆的焦点位置可由方程中含字母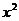、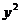项的分母的大小来确定，分母大的项对应的字母所在的轴就是焦点所在的轴. 而双曲线是根据项的正负来判断焦点所在的位置，即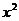项的系数是正的，那么焦点在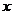轴上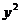；项的系数是正的，那么焦点在轴上.

8．双曲线的标准方程及特点：

(1)双曲线的标准方程有焦点在x轴上和焦点y轴上两种：

　 焦点在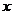轴上时双曲线的标准方程为：(,)；

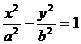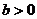　　 焦点在轴上时双曲线的标准方程为：(,)

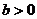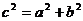(2)有关系式成立，且.

其中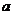与b的大小关系:可以为.

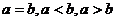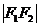7．双曲线的定义：平面内到两定点的距离的差的绝对值为常数(小于)的动点的轨迹叫双曲线.　 即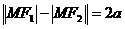. 这两个定点叫做双曲线的焦点，两焦点间的距离叫做焦距.

6.椭圆的参数方程.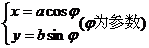

5.焦点到准线的距离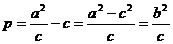(焦参数)

椭圆的准线方程有两条，这两条准线在椭圆外部，与短轴平行，且关于短轴对称.

4．椭圆的准线方程

对于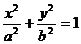，左准线；右准线.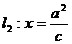

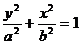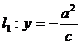对于，下准线；上准线.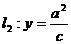

3.椭圆的第二定义:一动点到定点的距离和它到一条定直线的距离的比是一个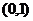内常数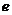，那么这个点的轨迹叫做椭圆. 其中定点叫做焦点，定直线叫做准线，常数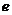就是离心率

椭圆的第二定义与第一定义是等价的，它是椭圆两种不同的定义方式.