
5.直线和抛物线
(1)位置关系:
相交(两个公共点或一个公共点);相离(无公共点);相切(一个公共点).
联立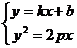 ,得关于x的方程
,得关于x的方程
当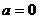 (二次项系数为零),唯一一个公共点(交点);
(二次项系数为零),唯一一个公共点(交点);
当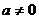 ,则
,则
若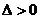 ,两个公共点(交点);
,两个公共点(交点);
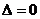 ,一个公共点(切点);
,一个公共点(切点);
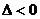 ,无公共点 (相离).
,无公共点 (相离).
(2)相交弦长:
弦长公式: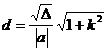 .
.
(3)焦点弦公式:
抛物线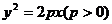 ,
,
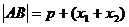 .
.
抛物线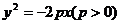 ,
,
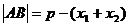 .
.
抛物线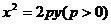 ,
,
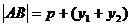 .
.
抛物线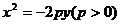 ,
,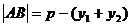 .
.
(4)通径:
定义:过焦点且垂直于对称轴的相交弦. 通径: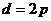 .
.
(5)常用结论:
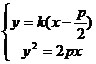
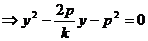 和
和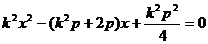
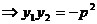 和
和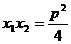 .
.
4.双曲线的通径:
定义:过焦点且垂直于对称轴的相交弦. 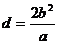 .
.
3.双曲线的焦点弦:
定义:过焦点的直线割双曲线所成的相交弦。
焦点弦公式:
当双曲线焦点在x轴上时,
过左焦点与左支交于两点时: 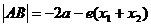 ;
;
过右焦点与右支交于两点时: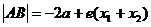 。
。
当双曲线焦点在y轴上时,
过左焦点与左支交于两点时: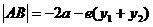 ;
;
过右焦点与右支交于两点时: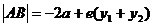 。
。
2.双曲线的焦半径
定义:双曲线上任意一点M与双曲线焦点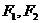 的连线段,叫做双曲线的焦半径.
的连线段,叫做双曲线的焦半径.
焦点在x轴上的双曲线的焦半径公式:
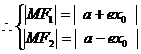
焦点在y轴上的双曲线的焦半径公式:
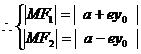 ( 其中
( 其中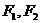 分别是双曲线的下上焦点)
分别是双曲线的下上焦点)
1.椭圆的焦半径公式:(左焦半径) ,(右焦半径)
,(右焦半径)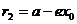 ,其中
,其中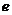 是离心率。 焦点在y轴上的椭圆的焦半径公式:
是离心率。 焦点在y轴上的椭圆的焦半径公式: 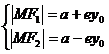 ( 其中
( 其中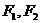 分别是椭圆的下上焦点).
分别是椭圆的下上焦点).
焦半径公式的两种形式的区别只和焦点的左右有关,而与点在左在右无关. 可以记为:左加右减,上减下加.
2.直线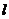 ∶Ax+B
∶Ax+B +C=0与圆锥曲线C∶f(x,y)=0的位置关系:
+C=0与圆锥曲线C∶f(x,y)=0的位置关系:
直线与圆锥曲线的位置关系可分为:相交、相切、相离.对于抛物线来说,平行于对称轴的直线与抛物线相交于一点,但并不是相切;对于双曲线来说,平行于渐近线的直线与双曲线只有一个交点,但并不相切.这三种位置关系的判定条件可引导学生归纳为:
设直线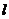 :Ax+By+C=0,圆锥曲线C:f(x,y)=0,由
:Ax+By+C=0,圆锥曲线C:f(x,y)=0,由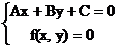
消去y(或消去x)得:ax2+bx+c=0,△=b2-4ac,(若a≠0时),
△>0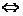 相交
△<0
相交
△<0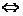 相离
△= 0
相离
△= 0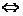 相切
相切
注意:直线与抛物线、双曲线有一个公共点是直线与抛物线、双曲线相切的必要条件,但不是充分条件.
1. 点M(x0,y0)与圆锥曲线C:f(x,y)=0的位置关系
已知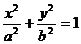 (a>b>0)的焦点为F1、F2,
(a>b>0)的焦点为F1、F2, 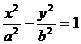 (a>0,b>0)
(a>0,b>0)
的焦点为F1、F2,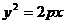 (p>0)的焦点为F,一定点为P(x0,y0),M点到抛物线的准线的距离为d,则有:
(p>0)的焦点为F,一定点为P(x0,y0),M点到抛物线的准线的距离为d,则有:

上述结论可以利用定比分点公式,建立两点间的关系进行证明.
6.线段AB过x轴正半轴上一点M(m,0)(m>0),端点A、B到x轴距离之积为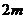 ,以x轴为对称轴,过A,O,B三点作抛物线.
,以x轴为对称轴,过A,O,B三点作抛物线.
(1)求抛物线方程;
(2)若 的取值范围.
的取值范围.
§7.3 点、直线和圆锥曲线
5.已知抛物线方程为 ,直线
,直线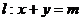 过抛物线的焦点F且被抛物线截得的弦长为3,求p的值.
过抛物线的焦点F且被抛物线截得的弦长为3,求p的值.
4.已知椭圆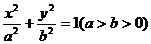 的离心率为
的离心率为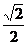 .(1)若圆(x-2)2+(y-1)2=
.(1)若圆(x-2)2+(y-1)2=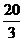 与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;(2)设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600,求
与椭圆相交于A、B两点且线段AB恰为圆的直径,求椭圆方程;(2)设L为过椭圆右焦点F的直线,交椭圆于M、N两点,且L的倾斜角为600,求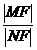 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com