
14.常见结论的否定形式
|
原结论 |
反设词 |
原结论 |
反设词 |
|
是 |
不是 |
至少有一个 |
一个也没有 |
|
都是 |
不都是 |
至多有一个 |
至少有两个 |
|
大于 |
不大于 |
至少有 个 个 |
至多有(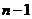 )个 )个 |
|
小于 |
不小于 |
至多有 个 个 |
至少有(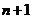 )个 )个 |
对所有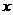 , ,成立 |
存在某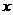 , ,不成立 |
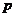 或 或 |
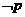 且 且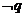 |
对任何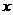 , ,不成立 |
存在某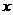 , ,成立 |
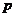 且 且 |
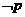 或 或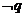 |
13.真值表
|
p |
q |
非p |
p或q |
p且q |
|
真 |
真 |
假 |
真 |
真 |
|
真 |
假 |
假 |
真 |
假 |
|
假 |
真 |
真 |
真 |
假 |
|
假 |
假 |
真 |
假 |
假 |
12.定区间上含参数的二次不等式恒成立的条件依据
(1)在给定区间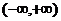 的子区间
的子区间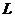 (形如
(形如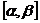 ,
,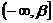 ,
,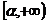 不同)上含参数的二次不等式
不同)上含参数的二次不等式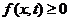 (
(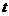 为参数)恒成立的充要条件是
为参数)恒成立的充要条件是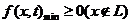 .
.
(2)在给定区间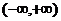 的子区间上含参数的二次不等式
的子区间上含参数的二次不等式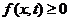 (
(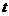 为参数)恒成立的充要条件是
为参数)恒成立的充要条件是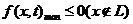 .
.
(3)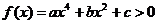 恒成立的充要条件是
恒成立的充要条件是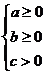 或
或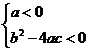 .
.
简易逻辑
11.一元二次方程的实根分布
依据:若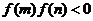 ,则方程
,则方程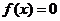 在区间
在区间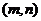 内至少有一个实根 .
内至少有一个实根 .
设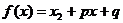 ,则
,则
(1)方程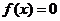 在区间
在区间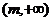 内有根的充要条件为
内有根的充要条件为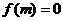 或
或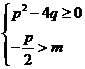 ;
;
(2)方程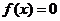 在区间
在区间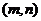 内有根的充要条件为
内有根的充要条件为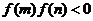 或
或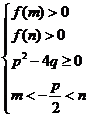 或
或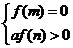 或
或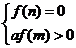 ;
;
(3)方程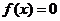 在区间
在区间 内有根的充要条件为
内有根的充要条件为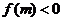 或
或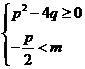 .
.
10.区间上的二次函数的最值
二次函数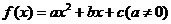 在闭区间
在闭区间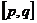 上的最值只能在
上的最值只能在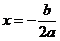 处及区间的两端点处取得,具体如下:
处及区间的两端点处取得,具体如下:
(1)当a>0时,若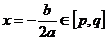 ,则
,则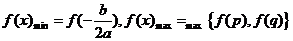 ;
;
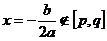 ,
,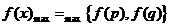 ,
,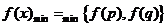 .
.
(2)当a<0时,若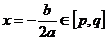 ,则
,则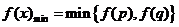 ,若
,若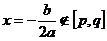 ,则
,则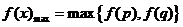 ,
,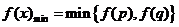 .
.
9.方程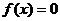 在
在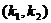 上有且只有一个实根,与
上有且只有一个实根,与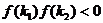 不等价,前者是后者的一个必要而不是充分条件.特别地, 方程
不等价,前者是后者的一个必要而不是充分条件.特别地, 方程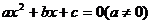 有且只有一个实根在
有且只有一个实根在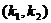 内,等价于
内,等价于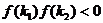 ,或
,或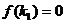 且
且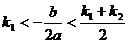 ,或
,或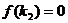 且
且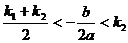 .
.
8.解连不等式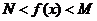 常有以下转化形式
常有以下转化形式
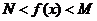

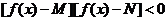

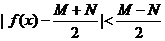

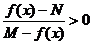

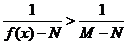 .
.
7.二次函数的解析式的三种形式
(1)一般式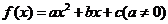 ;
;
(2)顶点式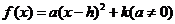 ;
;
(3)零点式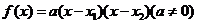 .
.
6.集合A中有M个元素,集合B中有N个元素,则可以构造M*N个从集合A到集合B的映射.
二次函数,二次方程
5.集合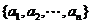 的子集个数共有
的子集个数共有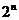 个;真子集有
个;真子集有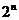 –1个;非空子集有
–1个;非空子集有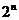 –1个;非空的真子集有
–1个;非空的真子集有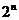 –2个.
–2个.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com