
24.几个常见的函数方程
(1)正比例函数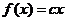 ,
,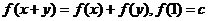 .
.
(2)指数函数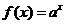 ,
, .
.
(3)对数函数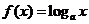 ,
,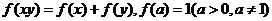 .
.
(4)幂函数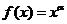 ,
,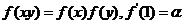 .
.
(5)余弦函数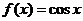 ,正弦函数
,正弦函数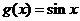 ,
,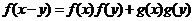 ,
,
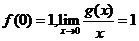 .
.
23.互为反函数的两个函数的关系
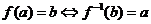 .
.
若函数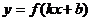 存在反函数,则其反函数为
存在反函数,则其反函数为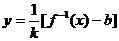 ,并不是
,并不是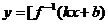 ,而函数
,而函数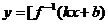 是
是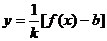 的反函数.
的反函数.
22.若将函数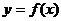 的图象右移
的图象右移 、上移
、上移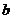 个单位,得到函数
个单位,得到函数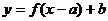 的图象;若将曲线
的图象;若将曲线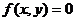 的图象右移
的图象右移 、上移
、上移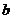 个单位,得到曲线
个单位,得到曲线 的图象.
的图象.
21.两个函数图象的对称性
(1)函数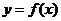 与函数
与函数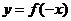 的图象关于直线
的图象关于直线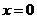 (即
(即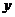 轴)对称.
轴)对称.
(2)函数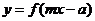 与函数
与函数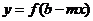 的图象关于直线
的图象关于直线 对称.
对称.
(3)函数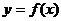 和
和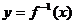 的图象关于直线y=x对称.
的图象关于直线y=x对称.
20.函数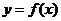 的图象的对称性
的图象的对称性
(1)函数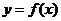 的图象关于直线
的图象关于直线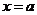 对称
对称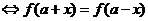
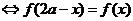 .
.
(2)函数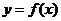 的图象关于直线
的图象关于直线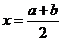 对称
对称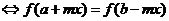
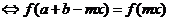 .
.
19.多项式函数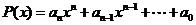 的奇偶性
的奇偶性
多项式函数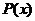 是奇函数
是奇函数
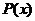 的偶次项(即奇数项)的系数全为零.
的偶次项(即奇数项)的系数全为零.
多项式函数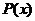 是偶函数
是偶函数
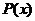 的奇次项(即偶数项)的系数全为零.
的奇次项(即偶数项)的系数全为零.
18.奇偶函数的图象特征
奇函数的图象关于原点对称,偶函数的图象关于y轴对称;在对称区间上,奇函数的单调性相同,欧函数相反;如果一个函数的图象关于原点对称,那么这个函数是奇函数;如果一个函数的图象关于y轴对称,那么这个函数是偶函数,如果一个奇函数的定义域包括0,则必有f(0)=0;
(1)若函数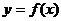 是偶函数,则
是偶函数,则 ;若函数
;若函数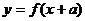 是偶函数,则
是偶函数,则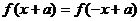 .
.
(2)对于函数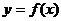 (
(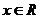 ),
),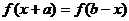 恒成立,则函数
恒成立,则函数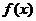 的对称轴是函数
的对称轴是函数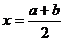 ;两个函数
;两个函数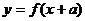 与
与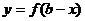 的图象关于直线
的图象关于直线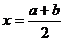 对称.
对称.
(3)若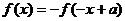 ,则函数
,则函数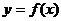 的图象关于点
的图象关于点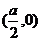 对称; 若
对称; 若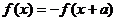 ,则函数
,则函数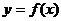 为周期为
为周期为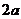 的周期函数.
的周期函数.
17.函数的单调性
(1)设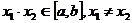 那么
那么
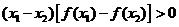

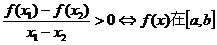 上是增函数;
上是增函数;
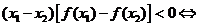
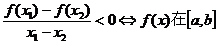 上是减函数.
上是减函数.
(2)设函数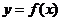 在某个区间内可导,如果
在某个区间内可导,如果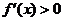 ,则
,则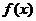 为增函数;如果
为增函数;如果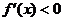 ,则
,则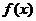 为减函数.
为减函数.
如果函数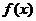 和
和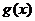 都是减函数,则在公共定义域内,和函数
都是减函数,则在公共定义域内,和函数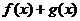 也是减函数; 如果函数
也是减函数; 如果函数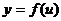 和
和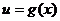 在其对应的定义域上都是减函数,则复合函数
在其对应的定义域上都是减函数,则复合函数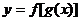 是增函数.
是增函数.
16.充要条件
(1)充分条件:若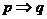 ,则
,则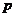 是
是 充分条件.
充分条件.
(2)必要条件:若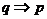 ,则
,则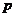 是
是 必要条件.
必要条件.
(3)充要条件:若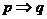 ,且
,且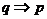 ,则
,则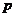 是
是 充要条件.
充要条件.
注:如果甲是乙的充分条件,则乙是甲的必要条件;反之亦然.
函数
15.四种命题的相互关系
原命题 互逆 逆命题
若p则q 若q则p
互 互
互 为 为 互
否 否
逆 逆
否 否
否命题 逆否命题
若非p则非q 互逆 若非q则非p
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com