
64.一元二次不等式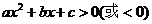
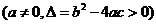 ,如果
,如果 与
与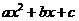 同号,则其解集在两根之外;如果
同号,则其解集在两根之外;如果 与
与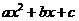 异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
异号,则其解集在两根之间.简言之:同号两根之外,异号两根之间.
 ;
;
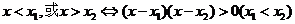 .
.
63.极值定理
已知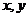 都是正数,则有
都是正数,则有
(1)若积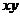 是定值
是定值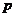 ,则当
,则当 时和
时和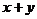 有最小值
有最小值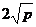 ;
;
(2)若和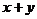 是定值
是定值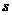 ,则当
,则当 时积
时积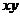 有最大值
有最大值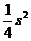 .
.
推广 已知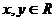 ,则有
,则有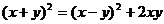
(1)若积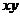 是定值,则当
是定值,则当 最大时,
最大时,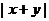 最大;
最大;
当 最小时,
最小时,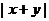 最小.
最小.
(2)若和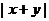 是定值,则当
是定值,则当 最大时,
最大时, 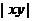 最小;
最小;
当 最小时,
最小时, 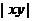 最大.
最大.
62.常用不等式:
(1)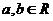

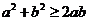 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(2)

 (当且仅当a=b时取“=”号).
(当且仅当a=b时取“=”号).
(3)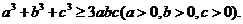
(4)柯西不等式
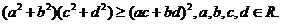
(5)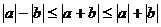 .
.
61.三角形五“心”向量形式的充要条件
设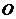 为
为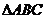 所在平面上一点,角
所在平面上一点,角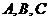 所对边长分别为
所对边长分别为 ,则
,则
(1)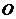 为
为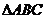 的外心
的外心 .
.
(2)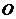 为
为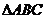 的重心
的重心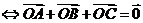 .
.
(3)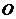 为
为 的垂心
的垂心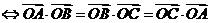 .
.
(4) 为
为 的内心
的内心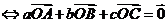 .
.
(5)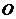 为
为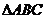 的
的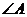 的旁心
的旁心 .
.
不等式
60.“按向量平移”的几个结论
(1)点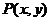 按向量a=
按向量a=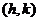 平移后得到点
平移后得到点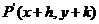 .
.
(2) 函数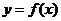 的图象
的图象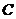 按向量a=
按向量a=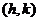 平移后得到图象
平移后得到图象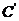 ,则
,则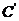 的函数解析式为
的函数解析式为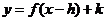 .
.
(3) 图象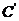 按向量a=
按向量a=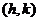 平移后得到图象
平移后得到图象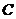 ,若
,若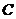 的解析式
的解析式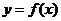 ,则
,则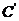 的函数解析式为
的函数解析式为 .
.
(4)曲线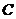 :
: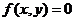 按向量a=
按向量a=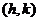 平移后得到图象
平移后得到图象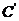 ,则
,则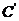 的方程为
的方程为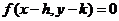 .
.
(5) 向量m= 按向量a=
按向量a=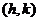 平移后得到的向量仍然为m=
平移后得到的向量仍然为m= .
.
59.点的平移公式

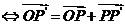 .
.
注:图形F上的任意一点P(x,y)在平移后图形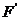 上的对应点为
上的对应点为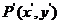 ,且
,且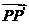 的坐标为
的坐标为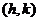 .
.
58.三角形的重心坐标公式
△ABC三个顶点的坐标分别为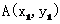 、
、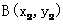 、
、 ,则△ABC的重心的坐标是
,则△ABC的重心的坐标是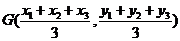 .
.
57.线段的定比分公式
设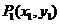 ,
,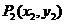 ,
,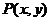 是线段
是线段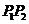 的分点,
的分点,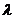 是实数,且
是实数,且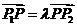 ,则
,则
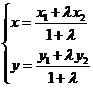



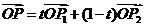 (
(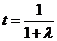 ).
).
56.向量的平行与垂直
设a=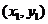 ,b=
,b= ,且b
,且b 0,则
0,则
A||b b=λa
b=λa  .
.
a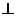 b(a
b(a 0)
0) a·b=0
a·b=0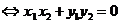 .
.
55.平面两点间的距离公式
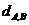 =
=
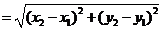 (A
(A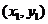 ,B
,B ).
).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com