
4.已知m、n为两条不同的直线,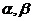 为两个不同的平面,下列四个命题中,错误的命题个数是 ( )
为两个不同的平面,下列四个命题中,错误的命题个数是 ( )
①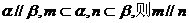 ;
;
②若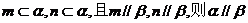 ;
;
③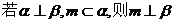 ;
;
④
A.1 B.2 C.3 D.4
3.曲线 在点(0,1)处的切线方程是 ( )
在点(0,1)处的切线方程是 ( )
A.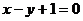 B.
B.
C. D.
D.
2.下列命题中真命题的个数是 ( )
①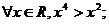
②若 是假命题,则p,q都是假命题;
是假命题,则p,q都是假命题;
③命题“ ”的否定是“
”的否定是“ ”
”
A.0 B.1 C.2 D.3
1.复数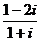 的虚部是 ( )
的虚部是 ( )
A.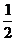 B.
B.
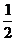 C.
C.
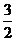 D.
D.
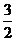 i
i
22.(本题满分14分)
已知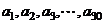 是首项为
是首项为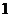 ,公比为
,公比为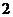 的等比数列.对于满足
的等比数列.对于满足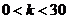 的整数
的整数 ,数列
,数列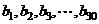 由
由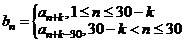 确定.记
确定.记
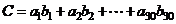 .
.
(Ⅰ)当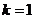 时,求
时,求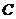 的值;
的值;
(Ⅱ) 求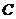 最小时
最小时 的值.
的值.
|
21.(本题满分12分)
已知函数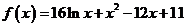 .
.
(Ⅰ)求函数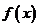 的单调区间;
的单调区间;
(Ⅱ)若直线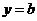 与函数
与函数 的图象有3个交点,求
的图象有3个交点,求 的取值范围.
的取值范围.
(注: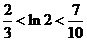 )
)
20.(本题满分12分)
设椭圆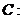
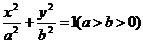 的离心率为
的离心率为 =
=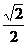 ,点
,点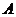 是椭圆
是椭圆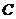 上的一点,且点
上的一点,且点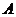 到椭圆
到椭圆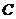 两焦点的距离之和为4.
两焦点的距离之和为4.
(Ⅰ)求椭圆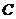 的方程;
的方程;
(Ⅱ)椭圆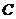 上一动点
上一动点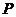
 关于直线
关于直线 的对称点为
的对称点为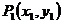 ,求
,求 的取值范围.
的取值范围.
19.(本题满分12分)
如图,五面体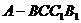 中,
中,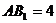 .底面
.底面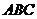 是正三角形,
是正三角形,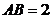 .四边形
.四边形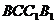 是矩形,平面
是矩形,平面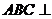 平面
平面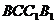 ,
,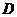 为
为 的中点.
的中点.
 (Ⅰ)证明
(Ⅰ)证明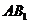 ∥平面
∥平面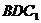 ;
;
(Ⅱ)求三棱锥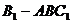 的体积.
的体积.
18.(本题满分12分)
田忌和齐王赛马是历史上著名的故事.设齐王的三匹马分别记为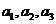 ,田忌的三匹马分别记为
,田忌的三匹马分别记为 ,三匹马各比赛一场,胜两场者获胜.若这六匹马比赛优劣程度可用不等式
,三匹马各比赛一场,胜两场者获胜.若这六匹马比赛优劣程度可用不等式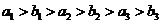 表示.
表示.
(Ⅰ)如果双方均不知道比赛的对阵方式,求田忌获胜的概率;
(Ⅱ)田忌为了得到更大的获胜概率,预先派出探子到齐王处打探实情,得知齐王第一场必出上等马,那么,田忌应该怎样安排出马顺序,才能使自己获胜的概率最大?最大概率是多少?
|
17.(本题满分12分)
在 中,角
中,角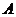 、
、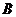 、
、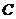 的对边分别为
的对边分别为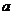 、
、 、
、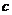 ,且
,且 .
.
(Ⅰ)求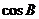 的值;
的值;
(Ⅱ)若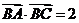 ,且
,且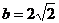 ,求
,求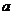 和
和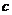 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com