
1.利用指示剂的变色情况进行酸、碱的判断;以常见的酸、碱的物理性质,考查物质的俗名、保存、取用等;如例1。
3.掌握氢氧化钠和氢氧化钙的性质和用途以及碱的通性和原理。
2.掌握盐酸、硫酸的性质和用途以及酸的通性和原理;
1.了解常见的指示剂及其与酸、碱作用的变色情况;
3.公式应用
例1
已知两点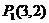 、
、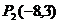 .求点
.求点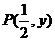 分
分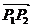 所成比
所成比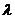 及
及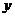 的值.
的值.
解:由线段定比分点坐标公式,得
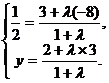 解得
解得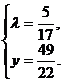
例2
如图,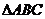 三个顶点的坐标分别为
三个顶点的坐标分别为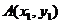 、
、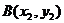 、
、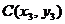 ,
,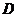 是边
是边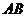 的中点,
的中点, 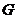 是
是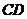 上一点,且
上一点,且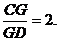 求点
求点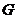 的坐标.
的坐标.
解: 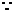
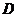 是边
是边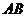 的中点,
的中点,

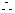 点
点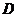 的坐标为
的坐标为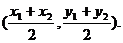
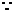
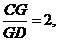
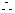
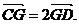
由定比分点坐标公式可得点 的坐标为
的坐标为
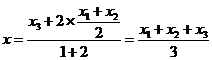
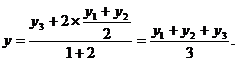
即点 的坐标为
的坐标为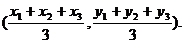
例3
已知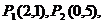
 在
在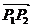 的延长线上,且
的延长线上,且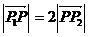 ,求点
,求点 的坐标.
的坐标.
解:设点 的坐标为
的坐标为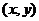 ,由已知
,由已知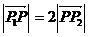 ,且
,且 在
在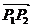 的延长线上,得
的延长线上,得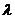 =-2.
=-2.
则
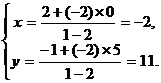 所以点
所以点 的坐标为
的坐标为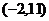
练习:教材117页
作业:117页习题1、2、3、5
2.定比分点的坐标公式
若已知点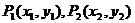 ,点
,点 是有向线段
是有向线段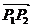 以
以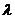 为定比的定比分点,求点
为定比的定比分点,求点 的坐标.
的坐标.
分析:设点 的坐标为
的坐标为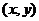 ,则向量
,则向量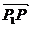 和
和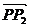 的坐标可求,据
的坐标可求,据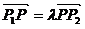 可得坐标间的关系,从而解出
可得坐标间的关系,从而解出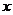 ,
,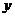 .
.
求解过程:(学生自己推导)
设点 的坐标为
的坐标为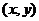 ,则
,则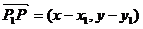 ,
,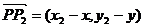 ,
,
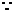
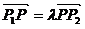
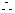
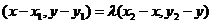
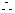
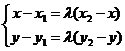 ,解得
,解得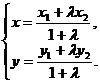 我们把所得结果叫有向线段
我们把所得结果叫有向线段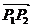 的定比分点坐标公式.
的定比分点坐标公式.
(其中: 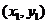 为起点坐标,
为起点坐标, 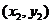 为终点坐标,
为终点坐标, 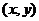 为分点坐标.)
为分点坐标.)
这说明,只要知道点 分
分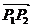 所成比
所成比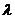 就可求得点
就可求得点 的坐标.
的坐标.
问:当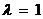 时,
时,  点的位置如何?并求
点的位置如何?并求 点的坐标.
点的坐标.
因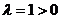 ,点
,点 在线段
在线段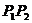 上,且
上,且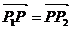 ,所以
,所以 是线段
是线段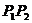 的中点.而且有
的中点.而且有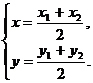
我们把所得结果叫做有向线段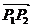 的中点坐标公式.
的中点坐标公式.
1.定比分点的定义
在直线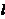 上取两点
上取两点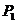 、
、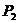 ,得到
,得到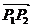 ,点
,点 是
是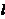 上不同于
上不同于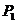 、
、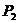 的任意一点,这时由点
的任意一点,这时由点 分得的两个有向线段我们记作:
分得的两个有向线段我们记作: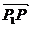 和
和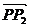 ,显然用
,显然用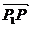 和
和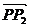 表示的两个向量共线,利用向量共线定理,则存在一个实数
表示的两个向量共线,利用向量共线定理,则存在一个实数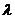 ,使得
,使得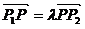 ,这时我们把
,这时我们把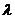 叫做点
叫做点 分有向线段
分有向线段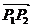 所成的比,点
所成的比,点 叫做有向线段
叫做有向线段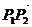 以
以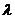 为定比的定比分点.
为定比的定比分点.
考虑: 点 的位置和
的位置和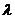 的符号有何关系?
的符号有何关系?
①点 在线段
在线段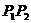 上,即
上,即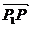 与
与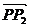 同向时,
同向时, 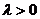 .这时称点
.这时称点 为
为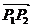 的内分点.
的内分点.
②点 在线段
在线段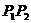 或
或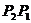 的延长线上,即
的延长线上,即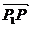 与
与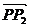 方向相反时,
方向相反时, 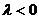 .这时称点
.这时称点 为
为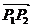 的外分点.
的外分点.
注: ①点 分
分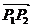 所得的有向线段是
所得的有向线段是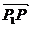 和
和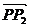 .(方向分别为起点到分点,分点到终点)
.(方向分别为起点到分点,分点到终点)
②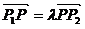 ,说明点
,说明点 和
和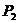 一定不能重合. ③当
一定不能重合. ③当 和
和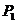 重合时
重合时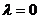 .
.
1. 重点: 线段的定比分点坐标公式和中点坐标公式的应用。
2.过程与方法
(1) 由向量共线定理引出一点 分一条有向线段
分一条有向线段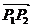 所成比的定义和定比分点的定义,进而得出定比分点坐标公式和中点坐标公式;
所成比的定义和定比分点的定义,进而得出定比分点坐标公式和中点坐标公式;
(2) 利用公式解决实际问题达到熟记公式的目的。
[教学重点、难点]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com