
7.已知函数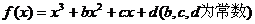 ,当
,当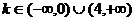 时,
时,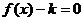 只有一个实数根;当
只有一个实数根;当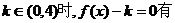 3个相异实根,现给出下列4个命题:
3个相异实根,现给出下列4个命题:
①函数 有2个极值点; ②函数
有2个极值点; ②函数 有3个极值点;
有3个极值点;
③ =4,
=4,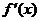 =0有一个相同的实根 ④
=0有一个相同的实根 ④ =0和
=0和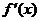 =0有一个相同的实根
=0有一个相同的实根
其中正确命题的个数是 ( )
A.1 B.2 C.3 D.4
6.若方程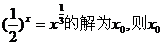 属于以下区间 ( )
属于以下区间 ( )
A.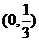 B.
B.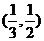 C.
C.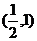 D.(1,2)
D.(1,2)
5.一个几何体的三视图如图所示,其中正视图中△ABC的边长为2的正三角形,俯视图为
正六边形,那么该几何体的侧视图的面积为 ( )
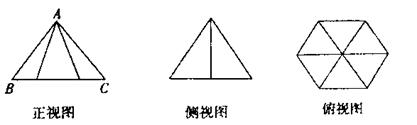
A.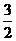 B.
B.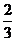 C.12 D.6
C.12 D.6
4.设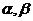 为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
为两个不重合的平面,l,m,n为两两不重合的直线,给出下列四个命题:
①若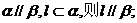 ②若
②若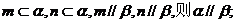
③若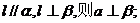 ④
④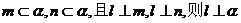 其中真命题的序号是 ( )
其中真命题的序号是 ( )
A.①③④ B.①②③ C.①③ D.②④
3.已知函数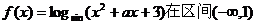 上递增,则实数a的取值范围是( )
上递增,则实数a的取值范围是( )
A.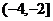 B.[-4,-2] C.(-4,+
B.[-4,-2] C.(-4,+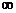 ) D.(-
) D.(-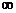 ,-2)
,-2)
2.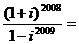 ( )
( )
A.22009i B.21004 C.21003(1+i) D.22008(1-i)
1.已知集合M是函数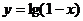 的定义域,集合
的定义域,集合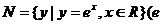 为自然对数的底数),则
为自然对数的底数),则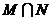 = ( )
= ( )
A.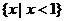 B.
B.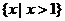 C.
C.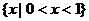 D.
D.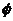
22.(文)(本小题满分14分)设数列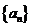 的前
的前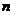 项和为
项和为 ,点
,点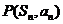 在直线
在直线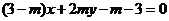 上,
上,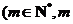 为常数,
为常数,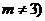 .
.
(Ⅰ)求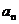 ;
;
(Ⅱ)若数列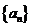 的公比
的公比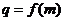 ,数列
,数列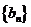 满足
满足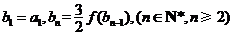 ,求证:
,求证: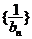 为等差数列,并求
为等差数列,并求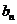 ;
;
(III)设数列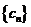 满足
满足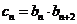 ,
,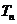 为数列
为数列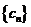 的前
的前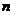 项和,且存在实数
项和,且存在实数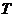 满足
满足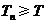 ,
,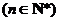 ,求
,求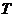 的最大值.
的最大值.
(理)(本小题满分14分)已知函数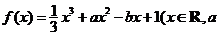 ,
,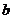 为实数)有极值,且在
为实数)有极值,且在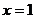 处的切线与直线
处的切线与直线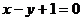 平行.
平行.
(1)求实数a的取值范围;
(2)是否存在实数a,使得函数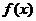 的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
的极小值为1,若存在,求出实数a的值;若不存在,请说明理由;
(3)设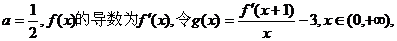
求证: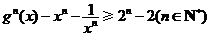 .
.
21.(文)(本小题满分12分)已知椭圆的中心在原点,焦点在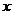 轴上,一个顶点为
轴上,一个顶点为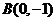 ,且其右焦点到直线
,且其右焦点到直线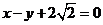 的距离为
的距离为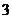 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)是否存在斜率为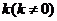 ,且过定点
,且过定点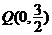 的直线
的直线 ,使
,使 与椭圆交于两个不同的点
与椭圆交于两个不同的点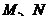 ,且
,且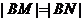 ?若存在,求出直线
?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(理)(本小题满分12分)已知抛物线的顶点在原点,焦点在y轴的负半轴上,过其上一点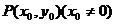 的切线方程为
的切线方程为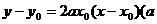 为常数).
为常数).
(I)求抛物线方程;
(II)斜率为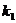 的直线PA与抛物线的另一交点为A,斜率为
的直线PA与抛物线的另一交点为A,斜率为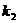 的直线PB与抛物线的另一交点为B(A、B两点不同),且满足
的直线PB与抛物线的另一交点为B(A、B两点不同),且满足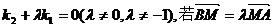 ,求证线段PM的中点在y轴上;
,求证线段PM的中点在y轴上;
(III)在(II)的条件下,当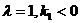 时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
时,若P的坐标为(1,-1),求∠PAB为钝角时点A的纵坐标的取值范围.
20.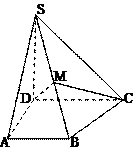 (文)(本小题满分12分)如图,在直角梯形
(文)(本小题满分12分)如图,在直角梯形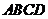 中,
中,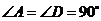 ,
,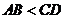 ,
,  平面
平面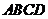 ,
,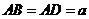 ,
,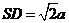 .
.
(Ⅰ)求证:平面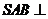 平面
平面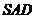 ;
;
(Ⅱ)设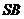 的中点为
的中点为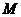 ,当
,当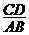 为何值时,
为何值时,
能使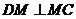 ? 请给出证明.
? 请给出证明.
 (理)(本小题满分12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠
(理)(本小题满分12分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠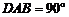 , AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
, AB∥CD,AD=CD=2AB=2,E,F分别是PC,CD的中点.
(Ⅰ)证明:CD⊥平面BEF;
(Ⅱ)设 ,
,
求k的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com