
19.(文)(本小题满分12分)某公司是一家专做产品A的国内外销售的企业,第一批产品A上市销售40天内全部售完,该公司对第一批产品A上市后的国内外市场销售情况进行了跟踪调查,调查结果如图所示,其中图①中的折线表示的是国外市场的日销售量与上市时间的关系;图②中的抛物线表示的是国内市场的日销售量与上市时间的关系;图③中折线表示的是每件产品A的销售利润与上市时间的关系(国内外市场相同).
(Ⅰ)分别写出国外市场的日销售量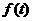 、国内市场的日销售量
、国内市场的日销售量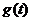 与第一批产品A 上市时间
与第一批产品A 上市时间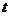 的关系式;
的关系式;
(Ⅱ)第一批产品A上市后的哪几天,这家公司的日销售利润超过6300万元?
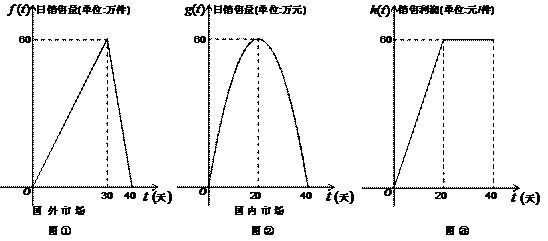
(理)
数列 中,
中,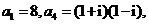 且满足
且满足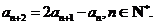
(Ⅰ)求数列 的通项公式;
的通项公式;
(Ⅱ)设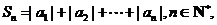 求
求 的解析式;
的解析式;
(Ⅲ)设计一个求 的程序框图.
的程序框图.
18.(文)(本小题满分12分)已知函数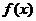 的定义域是
的定义域是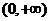 ,当
,当 时,
时,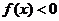 ,且
,且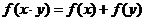 .
.
(Ⅰ)证明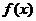 在定义域上是减函数;
在定义域上是减函数;
(Ⅱ)如果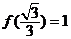 ,求满足不等式
,求满足不等式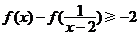 的
的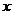 的取值范围.
的取值范围.
(理)(本小题满分12分)在2006年多哈亚运会中,中国女排与日本女排以“五局三胜”制进行决赛,根据以往战况,中国女排每一局赢的概率为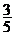 .已知比赛中,第一局日本女排先胜一局,在这个条件下,
.已知比赛中,第一局日本女排先胜一局,在这个条件下,
(Ⅰ)求中国女排取胜的概率;
(Ⅱ)设决赛中比赛总的局数为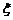 ,求
,求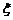 的分布列及
的分布列及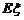 .(两问均用分数作答)
.(两问均用分数作答)
17.(本小题满分12分)
已知向量
(Ⅰ)求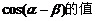 .
.
(Ⅱ)若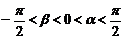 ,且
,且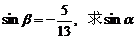 的值.
的值.
16.(文)设函数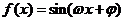 ,
,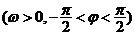 ,给出以下四个论断:
,给出以下四个论断:
①它的周期为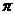 ;②它的图象关于直线
;②它的图象关于直线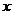 =
= 对称;③它的图象关于点(
对称;③它的图象关于点(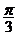 ,0)对称④在区间(
,0)对称④在区间(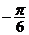 ,0)上是增函数.以其中两个论断为条件,另两个论断作结论,写出你认为正确的一个命题: 条件__________结论___________.(注:填上你认为正确的一种答案即可).
,0)上是增函数.以其中两个论断为条件,另两个论断作结论,写出你认为正确的一个命题: 条件__________结论___________.(注:填上你认为正确的一种答案即可).
(理)给出下列四个命题:
①  ;
;
②已知 ,则
,则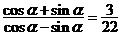
③曲线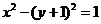 按
按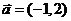 平移可得曲线
平移可得曲线 ;
;
④已知数列{an}是递增数列,且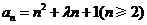 ,则实数
,则实数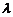 的取值范围是
的取值范围是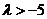 ;
;
其中真命题的序号为_________.(写出所有真命题的序号)
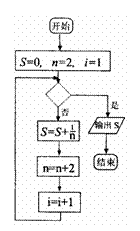
15.(文)如右图所示给出的是计算
的值的一个程序框图,其中判断框内填入的条件
是________________________ .

(理)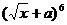 的展开式中x2项的系数为60,则实数a= .
的展开式中x2项的系数为60,则实数a= .
14.(文)数列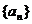 是正项等差数列,若
是正项等差数列,若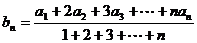 ,则数列
,则数列 也为等差数列. 类比上述结论,写出正项等比数列
也为等差数列. 类比上述结论,写出正项等比数列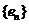 ,若
,若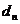 =
_________,则数列{
=
_________,则数列{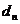 }也为等比数列.
}也为等比数列.
(理)在平面几何中:ΔABC的∠C的内角平分线CE分AB所成线段的比为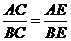 .把这个结论类比到空间:在三棱锥A-BCD中(如下图),DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是_________.
.把这个结论类比到空间:在三棱锥A-BCD中(如下图),DEC平分二面角A-CD-B且与AB相交于E,则得到类比的结论是_________.

13.(文)设动点P的坐标为(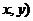 ,向量a=(x,0),b=(1,
,向量a=(x,0),b=(1,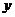 ),(
),(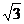 a+ b)⊥(
a+ b)⊥(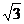 a-b).则点P的轨迹方程为____________.
a-b).则点P的轨迹方程为____________.
(理)已知变量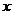 ,
,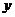 满足
满足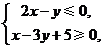 则
则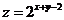 的最大值为__________.
的最大值为__________.
12.(文)已知定义在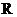 上的奇函数
上的奇函数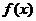 在区间
在区间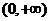 上单调递增,若
上单调递增,若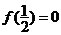 ,
, 的内角
的内角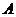 满足
满足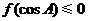 ,则角
,则角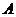 的取值范围是( )
的取值范围是( )
A.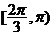 B.
B. 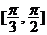 C.
C. D.
D.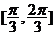
(理)已知偶函数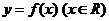 满足
满足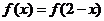 ,且当
,且当 时,
时,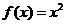 ,则函数
,则函数 与
与 的图象的交点个数为( )
的图象的交点个数为( )
A.3 B.4 C.6 D.5
10.(文)给出如下四个命题:①对于任意一条直线 ,平面
,平面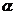 内必有无数条直线与
内必有无数条直线与 垂直;②若
垂直;②若 是两个不重合的平面,
是两个不重合的平面, 是两条不重合的直线,则
是两条不重合的直线,则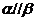 的一个充分而不必要条件是
的一个充分而不必要条件是 ,且
,且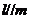 ;③已知
;③已知 是四条不重合的直线,如果
是四条不重合的直线,如果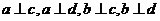 ,则
,则  不可能都不成立;④已知命题P:若四点不共面,那么这四点中任何三点都不共线.则命题P的逆否命题是假命题上命题中,正确命题的个数是( )
不可能都不成立;④已知命题P:若四点不共面,那么这四点中任何三点都不共线.则命题P的逆否命题是假命题上命题中,正确命题的个数是( )
A.3 B.2 C.1 D.0
(理)把函数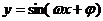 (其中
(其中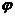 是锐角)的图象向右平移
是锐角)的图象向右平移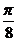 个单位,或向左平移
个单位,或向左平移 个单位都可以使对应的新函数成为奇函数,则
个单位都可以使对应的新函数成为奇函数,则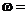 ( )
( )
A.2 B.3 C.4 D.1
11 (文)中心在原点,焦点坐标为
(文)中心在原点,焦点坐标为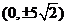 的椭圆被直线
的椭圆被直线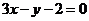 截得的弦的中点的横坐标为
截得的弦的中点的横坐标为 ,则椭圆方程为(
)
,则椭圆方程为(
)
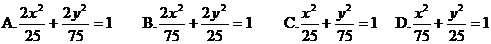
(理)过双曲线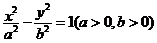 的左焦点F1,作圆
的左焦点F1,作圆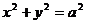 的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下正确的是( )
的切线交双曲线右支于点P,切点为T,PF1的中点M在第一象限,则以下正确的是( )
A.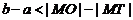 B.
B.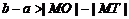
C. D.
D.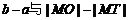 大小不定
大小不定
9.若直线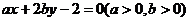 ,始终平分圆
,始终平分圆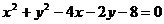 的周长,则
的周长,则 的最小值为( )
的最小值为( )
A.1 B.5
C. D.
D.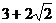
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com