
21、★★已知函数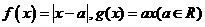 (1)判断函数
(1)判断函数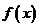 的对称性和奇偶性;(2)当
的对称性和奇偶性;(2)当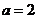 时,求使
时,求使 成立的
成立的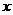 的集合;(3)若
的集合;(3)若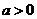 ,记
,记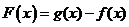 ,且
,且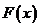 在
在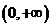 有最大值,求
有最大值,求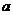 的取值范围.
的取值范围.
解析:(1)由函数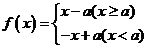 可知,函数
可知,函数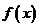 的图象关于直线
的图象关于直线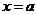 对称;
对称;
当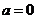 时,函数
时,函数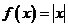 是一个偶函数;当
是一个偶函数;当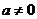 时,取特值:
时,取特值: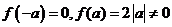 ,故函数
,故函数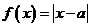 是非奇非偶函数.
是非奇非偶函数.
(2)由题意得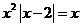 ,得
,得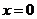 或
或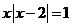 ;因此得
;因此得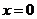 或
或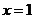 或
或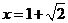 ,故所求的集合为
,故所求的集合为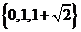 .
.
(3)对于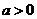 ,
,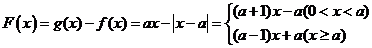
若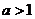 ,
,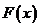 在区间
在区间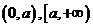 上递增,无最大值;
上递增,无最大值;
若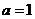 ,
,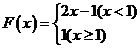 有最大值1
有最大值1
若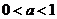 ,
,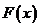 在区间
在区间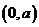 上递增,在
上递增,在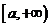 上递减,
上递减,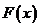 有最大值
有最大值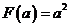 ;
;
综上所述得,当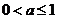 时,
时,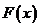 有最大值.
有最大值.
20、已知向量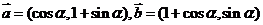 ,(1)若
,(1)若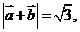 求
求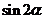 的值;(2)设
的值;(2)设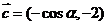 ,求
,求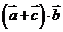 的取值范围.
的取值范围.
解析:(1)因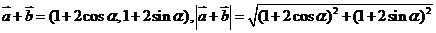
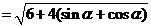 ,
,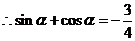 ,两边平方得
,两边平方得 ,
,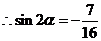
(2)因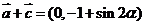 ,
,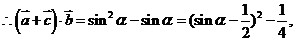 又
又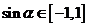 ,
,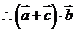 的取值范围为
的取值范围为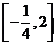 .
.
19、规定记号“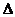 ”表示一种运算,即
”表示一种运算,即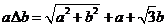 ,记
,记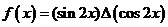 .(1)求函数
.(1)求函数 的表达式;(2)求函数
的表达式;(2)求函数 的最小正周期;(3)若函数
的最小正周期;(3)若函数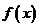 在
在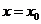 处取到最大值,求
处取到最大值,求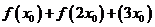 的值
的值
解析:(1)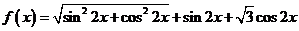
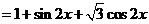 ;
;
(2)因 ,因此
,因此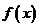 的最小正周期为
的最小正周期为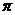 ;
;
(3)由题意,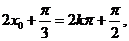 即
即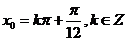 ;因此
;因此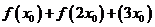 =
=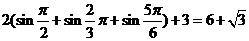
18、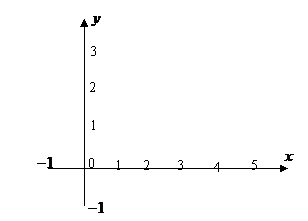 已知函数
已知函数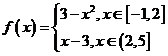 ,(1)在如图给定的直角坐标系内画出
,(1)在如图给定的直角坐标系内画出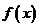 的图象;(2)写出
的图象;(2)写出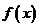 的单调递增区间.
的单调递增区间.
 解析:(1)函数
解析:(1)函数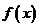 的图象如图所示:
的图象如图所示:
(2)函数的单调递增区间为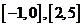
17、已知集合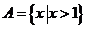 ,集合B=
,集合B=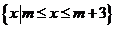 ;(1)当
;(1)当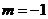 时,求
时,求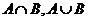 ;(2)若
;(2)若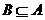 ,求
,求 的取值范围.
的取值范围.
解析:(1)当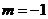 时,
时,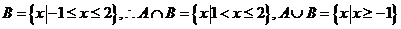 ;
;
(2)若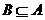 ,则
,则 的取值范围为
的取值范围为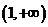 .
.
16、★如图,点P是单位圆上的一个顶点,它从初始位置 开始沿单位圆按逆时针方向运动角
开始沿单位圆按逆时针方向运动角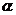 (
(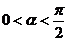 )到达点
)到达点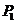 ,然后继续沿单位圆逆时针方向运动
,然后继续沿单位圆逆时针方向运动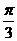 到达点
到达点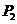 ,若点
,若点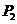 的横坐标为
的横坐标为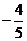 ,则
,则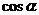 的值等于
的值等于
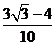 解析:因为
解析:因为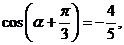 因此
因此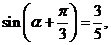
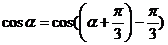
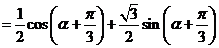 =
=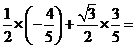
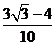
15、★如果若干个函数的图象经过平移后能够重合,则这些函数为“互为生成”函数,给出下列函数:(1)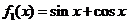 ;(2)
;(2) ;(3)
;(3)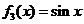 ;(4)
;(4)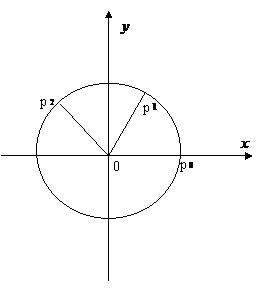
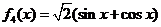 ;(5)
;(5)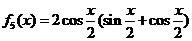 ,其中“互为生成”函数有
(把所有可能的函数的序号都填上)
,其中“互为生成”函数有
(把所有可能的函数的序号都填上)
(1)(2)(5)解析:对于(1)(2)(5)通过平移均可办到,而(3)(4)还需要纵坐标进行伸长和缩短.
14、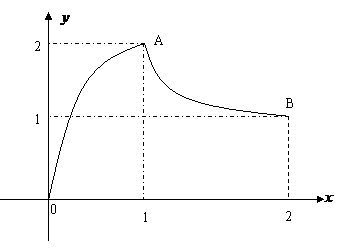 如图,函数
如图,函数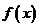 的图象是曲线OAB,其中点O,A,B的坐标分别为
的图象是曲线OAB,其中点O,A,B的坐标分别为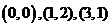 ,则
,则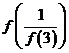 的值等于
的值等于
 解析:对于
解析:对于
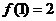
13、设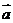 与
与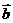 是两个不共线的向量,且向量
是两个不共线的向量,且向量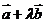 与
与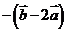 共线,则
共线,则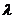 的值等于
的值等于
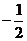 解析:因为
解析:因为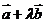 与
与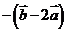 共线,则有
共线,则有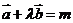
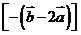 ,即有
,即有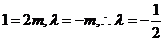 .
.
12、函数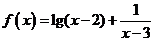 的定义域是
的定义域是
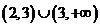 解析:对于
解析:对于 ,因此函数
,因此函数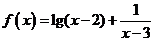 的定义域是
的定义域是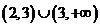 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com