
8.(文)设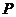 、
、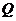 为两个非空实数集合,定义集合
为两个非空实数集合,定义集合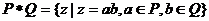 ,若
,若
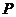 ={-1,0,1},
={-1,0,1},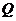 ={-2,2},则集合
={-2,2},则集合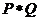 中元素的个数是( )
中元素的个数是( )
A.2 B.3 C.4 D.5
(理)已知集合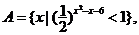
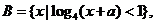 若
若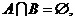 则实数a的取值范围是( )
则实数a的取值范围是( )
A.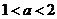 B.
B.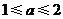 C.
C.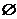 D.
D.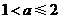
7.
已知函数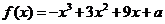 (a为常数),在区间
(a为常数),在区间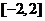 上有最大值20,那么此函数在区间
上有最大值20,那么此函数在区间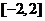 上的最小值为( )
上的最小值为( )
A.
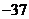 B.
B.
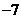 C.
C.
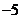 D.
D. 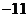
6.(文)下列四个命题 :
(1)线性相关系数r越大,两个变量的线性相关性越强;反之,线性相关性越弱;
(2)残差平方和越小的模型,模型拟和的效果越好;
(3)用相关指数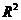 来刻画回归效果,
来刻画回归效果,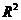 越小,说明模型的拟和效果越好;
越小,说明模型的拟和效果越好;
(4)在推断H:“X与Y有关系”的论述中,用三维柱形图,只要主对角线上两个柱形高度的比值与副对角线上的两个柱形高度的比值相差越大,H成立的可能性就越大.
其中真命题的个数是( )
A. 1 B. 2 C. 3 D. 4
(理)下列命题中,其中假命题是 ( )
A.对分类变量X与Y的随机变量K2的观测值k来说,k越小,“X与Y有关系”可信程度越大
B.用相关指数R2来刻画回归的效果时,R2的值越大,说明模型拟合的效果越好
C.两个随机变量相关性越强,则相关系数的绝对值越接近1
D.三维柱形图中柱的高度表示的是各分类变量的频数
5.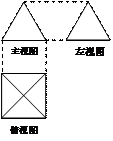 如下图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是( )
如下图,一个简单空间几何体的三视图其主视图与左视图都是边长为2的正三角形,其俯视图轮廓为正方形,则其体积是( )
A.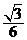 B .
B . 
C. 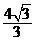 D .
D . 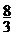
4.(文)已知正三棱锥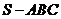 的底面边长为4,高为3,在正三棱锥内任取一点
的底面边长为4,高为3,在正三棱锥内任取一点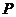 ,使得
,使得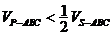 的概率是( )
的概率是( )
A.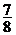 B.
B. C.
C.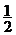 D.
D.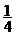
(理)两位大学毕业生一起去一家单位应聘,面试前单位负责人对他们说:“我们要从面试的人中招聘3人,你们俩同时被招聘进来的概率是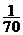 ”,根据这位负责人的话可以推断出参加面试的人数为( )
”,根据这位负责人的话可以推断出参加面试的人数为( )
A.21 B.35 C.42 D.706
3.(文)一组数据的平均数是 ,方差是
,方差是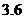 ,若将这组数据中的每一个数据都加上
,若将这组数据中的每一个数据都加上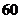 ,得到一组新数据,则所得新数据的平均数和方差分别是( )
,得到一组新数据,则所得新数据的平均数和方差分别是( )
A.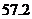
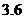 B.
B.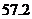
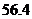 C.
C.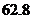
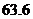 D.
D.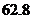
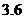
(理)已知点A(3,0),B(0,3),C(cosα,sinα),O(0,0),若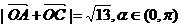 ,则
,则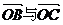 的夹角为( )
的夹角为( )
A.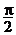 B.
B.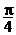 C.
C.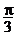 D.
D.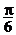
2.下列命题错误的是( )
A.命题“若m>0,则方程x2+x-m=0有实数根”的逆否命题为:“若方程x2+x-m=0
无实数根,则m≤0”.
B.“x =1”是“x2-3x+2=0”的充分不必要条件.
C.若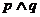 为假命题,则p ,q均为假命题.
为假命题,则p ,q均为假命题.
D.对于命题p: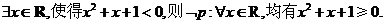
1.若复数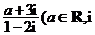 为虚数单位)是纯虚数,则实数a的值为( )
为虚数单位)是纯虚数,则实数a的值为( )
A.-2 B.4 C.-6 D.6
22、设三次函数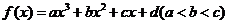 ,在
,在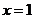 处取得极值,其图像在
处取得极值,其图像在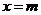 处的切线的斜率为
处的切线的斜率为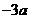 。
。
(1)求证: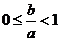 ;
;
(2)若函数 在区间
在区间 上单调递增,求
上单调递增,求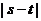 的取值范围;
的取值范围;
(3)问是否存在实数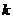 (
(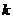 是与
是与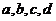 无关的常数),当
无关的常数),当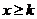 时,恒有
时,恒有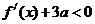 恒成立?若存在,试求出
恒成立?若存在,试求出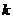 的最小值;若不存在,请说明理由。
的最小值;若不存在,请说明理由。
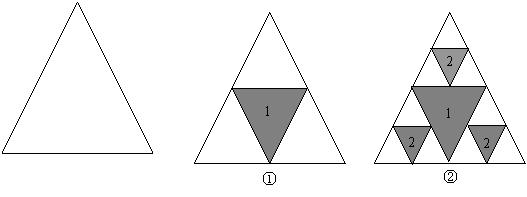
21、如图是一个面积为1的三角形,现进行如下操作。第一次操作:分别连接这个三角形三边的中点,构成4个三角形,挖去中间一个三角形(如图①中阴影部分所示),并在挖去的三角形上贴上数字标签“1”;第二次操作:连结剩余的三个三角形三边的中点,再挖去各自中间的三角形(如图②中阴影部分所示),同时在挖去的3个三角形上都贴上数字标签“2”;第三次操作:连接剩余的各三角形三边的中点,再挖去各自中间的三角形,同时在挖去的三角形上都贴上数字标签“3”;……,如此下去,记第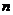 次操作后剩余图形的总面积为
次操作后剩余图形的总面积为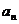
(1)求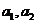 ;
;
(2)求第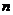 次操作后,挖去的所有三角形上所贴标签上的数字和
次操作后,挖去的所有三角形上所贴标签上的数字和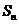 ;
;
(3)浴使剩余图形的总面积不足原三角形面积的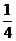 ,问至少经过多少次操作?
,问至少经过多少次操作?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com