
13.(2009辽宁卷理)平面向量a与b的夹角为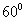 ,
,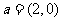 ,
,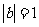 则
则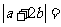
(A)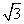 (B)
(B) 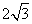 (C)
4
(D)12
(C)
4
(D)12
[解析]由已知|a|=2,|a+2b|2=a2+4a·b+4b2=4+4×2×1×cos60°+4=12
∴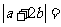
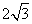
[答案]B
12.(2009全国卷Ⅱ理)已知向量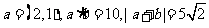 ,则
,则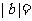


A.
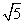 B.
B.
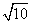 C.
C.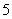 D.
D.
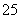
解: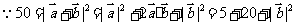
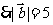 。故选C
。故选C
11.(2009湖北卷理)已知 是两个向量集合,则
是两个向量集合,则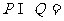
A.{(1,1)} B. {(-1,1)} C. {(1,0)} D. {(0,1)}
[答案]A
[解析]因为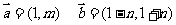 代入选项可得
代入选项可得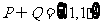 故选A.
故选A.
10.(2009全国卷Ⅰ理)设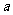 、
、 、
、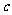 是单位向量,且
是单位向量,且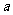 ·
· =0,则
=0,则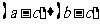 的最小值为 ( D
)
的最小值为 ( D
)
(A) (B)
(B)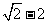 (C)
(C)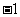 (D)
(D)
解: 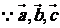 是单位向量
是单位向量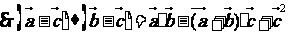


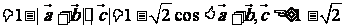 故选D.
故选D.
9.(2009全国卷Ⅱ文)已知向量a = (2,1), a·b = 10,︱a + b ︱= 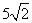 ,则︱b ︱=
,则︱b ︱=
(A)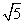 (B)
(B)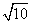 (C)5 (D)25
(C)5 (D)25
答案:C
解析:本题考查平面向量数量积运算和性质,由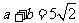 知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
知(a+b)2=a2+b2+2ab=50,得|b|=5 选C。
8.(2009山东卷理)设P是△ABC所在平面内的一点,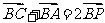 ,则( )
,则( )
A.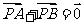 B.
B.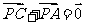 C.
C.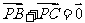 D.
D.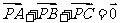
[解析]:因为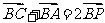 ,所以点P为线段AC的中点,所以应该选B。
,所以点P为线段AC的中点,所以应该选B。
答案:B。
[命题立意]:本题考查了向量的加法运算和平行四边形法则,
可以借助图形解答。
7.(2009北京卷理)已知向量a、b不共线,c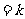 a
a b
b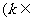 R),d
R),d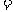 a
a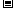 b,如果c
b,如果c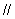 d,那么
( )
d,那么
( )
A.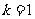 且c与d同向
B.
且c与d同向
B.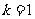 且c与d反向
且c与d反向
C.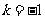 且c与d同向
D.
且c与d同向
D.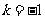 且c与d反向
且c与d反向
[答案]D
[解析]本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算的考查.
取a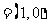 ,b
,b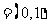 ,若
,若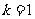 ,则c
,则c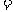 a
a b
b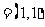 ,d
,d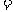 a
a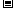 b
b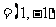 ,
,
显然,a与b不平行,排除A、B.
若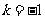 ,则c
,则c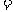
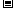 a
a b
b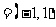 ,d
,d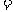
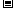 a
a b
b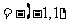 ,
,
即c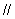 d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
5.(2009北京卷文)已知向量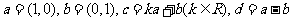 ,如果
,如果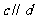 ,那么
,那么
A.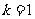 且
且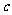 与
与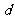 同向
B.
同向
B.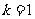 且
且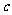 与
与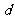 反向
反向
C.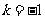 且
且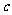 与
与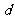 同向
D.
同向
D.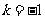 且
且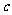 与
与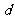 反向
反向
[答案]D
.w[解析].k.s.5.u.c本题主要考查向量的共线(平行)、向量的加减法. 属于基础知识、基本运算的考查.
∵a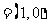 ,b
,b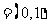 ,若
,若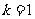 ,则c
,则c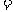 a
a b
b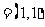 ,d
,d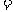 a
a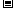 b
b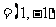 ,
,
显然,a与b不平行,排除A、B.
若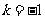 ,则c
,则c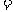
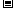 a
a b
b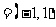 ,d
,d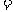
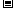 a
a b
b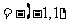 ,
,
即c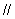 d且c与d反向,排除C,故选D.
d且c与d反向,排除C,故选D.
4.(2009浙江卷文)已知向量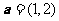 ,
,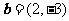 .若向量
.若向量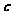 满足
满足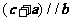 ,
,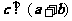 ,则
,则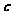
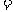 ( )
( )
A.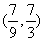 B.
B.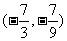 C.
C.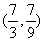 D.
D.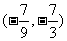
[命题意图]此题主要考查了平面向量的坐标运算,通过平面向量的平行和垂直关系的考查,很好地体现了平面向量的坐标运算在解决具体问题中的应用.
[解析]不妨设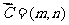 ,则
,则 ,对于
,对于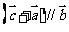 ,则有
,则有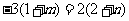 ;又
;又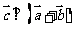 ,则有
,则有 ,则有
,则有
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com