
23.(2008泰州市)在矩形ABCD中,AB=2,AD=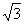 .
.
(1)在边CD上找一点E,使EB平分∠AEC,并加以说明;(3分)
(2)若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.
①求证:点B平分线段AF;(3分)
②△PAE能否由△PFB绕P点按顺时针方向旋转而得到,若能,加以证明,并求出旋转度数;若不能,请说明理由.(4分)
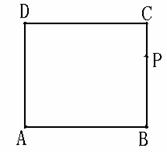
24.(2008 河南实验区)如图,已知:在四边形ABFC中, =90
=90 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
(1) 试探究,四边形BECF是什么特殊的四边形;
(2) 当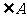 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(特别提醒:表示角最好用数字)

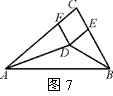
22.(.2008资阳市)如图7,在△ABC中,∠A、∠B的平分线交于点D,DE∥AC交BC于点E,DF∥BC交AC于点F.
(1)点D是△ABC的________心;
(2)求证:四边形DECF为菱形.

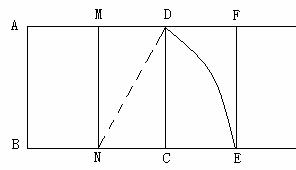
21.(2008湖北孝感)宽与长的比是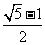 的矩形叫黄金矩形,心理学测试表明,黄金矩形令人赏心悦目,它给我们以协调、匀称的美感。现将同学们在教学活动中,折叠黄金矩形的方法归纳出以下作图步骤(如图所示):
的矩形叫黄金矩形,心理学测试表明,黄金矩形令人赏心悦目,它给我们以协调、匀称的美感。现将同学们在教学活动中,折叠黄金矩形的方法归纳出以下作图步骤(如图所示):
第一步:作一个任意正方形ABCD;
第二步:分别取AD、BC的中点M、N,连接MN;
第三步:以N为圆心,ND长为半径画弧,交BC的延长线于E;
第四步:过E作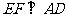 交AD的延长线于F ,
交AD的延长线于F ,
请你根据以上作法,证明矩形DCEF为黄金矩形,(可取AB=2)。
20. (2008湖北襄樊)如图12,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG、DE.
(2008湖北襄樊)如图12,B、C、E是同一直线上的三个点,四边形ABCD与四边形CEFG是都是正方形.连接BG、DE.
(1)观察猜想BG与DE之间的大小关系,并证明你的结论.
(2)在图中是否存在通过旋转能够互相重合的两个三角形?若存在,请指出,并说出旋转过程;若不存在,请说明理由.
19.(2008佳木斯市)有一底角为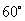 的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.
的直角梯形,上底长为10cm,与底垂直的腰长为10cm,以上底或与底垂直的腰为一边作三角形,使三角形的另一边长为15cm,第三个顶点落在下底上.请计算所作的三角形的面积.
18.(08厦门市)已知:如图所示的一张矩形纸片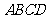 (
(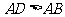 ),将纸片折叠一次,使点
),将纸片折叠一次,使点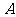 与
与 重合,再展开,折痕
重合,再展开,折痕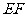 交
交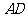 边于
边于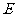 ,交
,交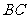 边于
边于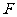 ,分别连结
,分别连结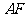 和
和 .
.
(1)求证:四边形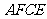 是菱形;
是菱形;
(2)若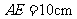 ,
, 的面积为
的面积为 ,求
,求 的周长;
的周长;
(3)在线段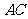 上是否存在一点
上是否存在一点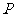 ,使得
,使得 ?
?
若存在,请说明点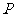 的位置,并予以证明;若不存在,请说明理由.
的位置,并予以证明;若不存在,请说明理由.
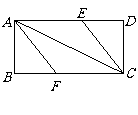
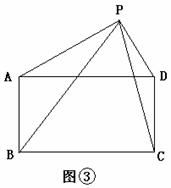
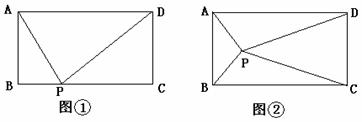
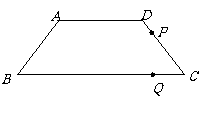
17.(08莆田市)已知矩形ABCD和点P,当点P在BC上任一位置(如图(1)所示)时,易证得结论: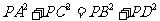 ,请你探究:当点P分别在图(2)、图(3)中的位置时,
,请你探究:当点P分别在图(2)、图(3)中的位置时, 又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论。
又有怎样的数量关系?请你写出对上述两种情况的探究结论,并利用图(2)证明你的结论。
答:对图(2)的探究结论为____________________________________.
对图(3)的探究结论为_____________________________________.
证明:如图(2)
16..(2008湖北咸宁)如图,在△ABC 中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的角平分线于点E,交∠BCA的外角平分线于点F.
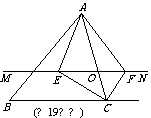
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形AECF是矩形?并证明你的结论.
15.(2008年江苏省连云港市)如图,在直角梯形纸片 中,
中, ,
,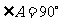 ,
, ,将纸片沿过点
,将纸片沿过点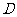 的直线折叠,使点
的直线折叠,使点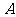 落在边
落在边 上的点
上的点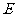 处,折痕为
处,折痕为 .连接
.连接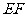 并展开纸片.
并展开纸片.
(1)求证:四边形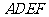 是正方形;
是正方形;
(2)取线段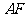 的中点
的中点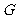 ,连接
,连接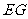 ,如果
,如果 ,试说明四边形
,试说明四边形 是等腰梯形.
是等腰梯形.
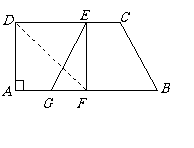

14. (2008年江苏省苏州市)如图,在等腰梯形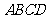 中,
中,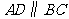 ,
, ,
, ,
,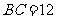 .动点
.动点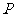 从
从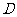 点出发沿
点出发沿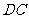 以每秒1个单位的速度向终点
以每秒1个单位的速度向终点 运动,动点
运动,动点 从
从 点出发沿
点出发沿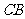 以每秒2个单位的速度向
以每秒2个单位的速度向 点运动.两点同时出发,当
点运动.两点同时出发,当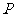 点到达
点到达 点时,
点时, 点随之停止运动.
点随之停止运动.
(1)梯形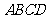 的面积等于
;
的面积等于
;
(2)当 时,
时,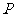 点离开
点离开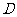 点的时间等于
秒;
点的时间等于
秒;
(3)当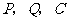 三点构成直角三角形时,
三点构成直角三角形时,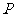 点离开
点离开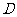 点多少时间?
点多少时间?

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com