
15. 证明:(1) ,
, ,
,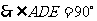 .
.
由沿 折叠后
折叠后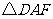 与
与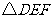 重合,知
重合,知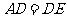 ,
,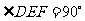 .
.
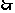 四边形
四边形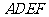 是矩形,且邻边
是矩形,且邻边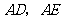 相等.
相等.
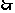 四边形
四边形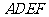 是正方形. 3分
是正方形. 3分
(2) ,且
,且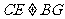 ,
,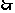 四边形
四边形 是梯形. 4分
是梯形. 4分
 四边形
四边形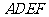 是正方形,
是正方形,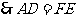 ,
,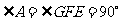 .
.
又点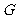 为
为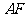 的中点,
的中点,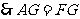 .连接
.连接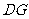 .
.
在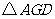 与
与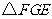 中,
中,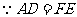 ,
,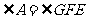 ,
,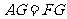 ,
,
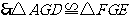 ,
,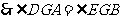 . 6分
. 6分
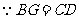 ,
,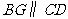 ,
,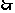 四边形
四边形 是平行四边形.
是平行四边形.
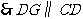 .
. .
.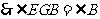 .
.
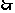 四边形
四边形 是等腰梯形. 8分
是等腰梯形. 8分
注:第(2)小题也可过点 作
作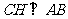 ,垂足为点
,垂足为点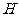 ,证
,证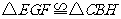
14. 解:(1)36;(2)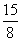 秒;
秒;
(3)当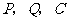 三点构成直角三角形时,有两种情况:
三点构成直角三角形时,有两种情况:
①当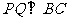 时,设
时,设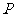 点离开
点离开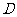 点
点 秒,
秒,
 作
作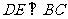 于
于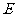 ,
,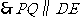 .
.
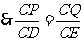 ,
,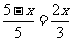 ,
,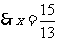 .
.
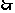 当
当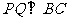 时,
时,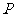 点离开
点离开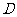 点
点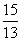 秒.
秒.
②当 时,设
时,设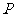 点离开
点离开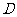 点
点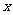 秒,
秒,
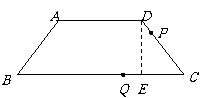
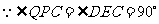 ,
,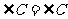 .
.
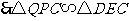 .
.
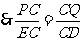 .
.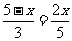 .
.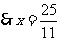 .
.
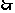 当
当 时,点
时,点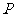 离开点
离开点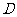
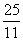 秒.
秒.
由①②知,当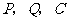 三点构成直角三角形时,点
三点构成直角三角形时,点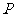 离开点
离开点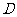
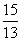 秒或
秒或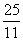 秒.
秒.
13. (1)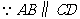 ,即
,即 ,又
,又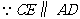 ,
,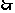 四边形
四边形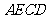 是平行四边形.
是平行四边形.
(2分)
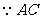 平分
平分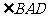 ,
,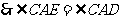 , (3分)
, (3分)
又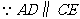 ,
,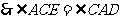 ,
,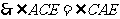 ,
,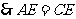 ,
,
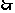 四边形
四边形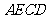 是菱形. (4分)
是菱形. (4分)
(2)证法一: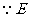 是
是 中点,
中点,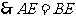 .
.
又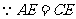 ,
,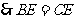 ,
,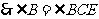 , (5分)
, (5分)
 , (6分)
, (6分)
 ,
, .
.
即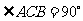 ,
,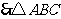 是直角三角形. (7分)
是直角三角形. (7分)
证法二:连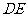 ,则
,则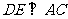 ,且平分
,且平分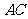 , (5分)
, (5分)
设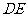 交
交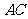 于
于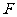 .
.
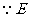 是
是 的中点,
的中点,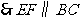 . (6分)
. (6分)
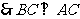 ,
,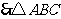 是直角三角形. (7分)
是直角三角形. (7分)
12. 解法一: 矩形
矩形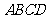 中,
中, ,
, , (2分)
, (2分)
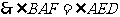 . (4分)
. (4分)
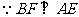 ,
,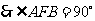 ,
,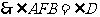 . (5分)
. (5分)
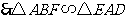 . (6分)
. (6分)
解法二: 矩形
矩形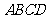 中,
中, . (2分)
. (2分)
 ,
,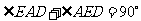 ,
,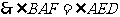 . (4分)
. (4分)
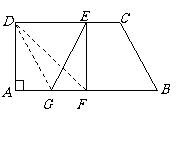
11. 解:(1)证明:∵四边形为正方形,∴BC=CD,∠BCG=∠DCE=90° 2分
∵CG=CE,∴△BCG≌△DCE. ………………4分
(2)答:四边形E′BGD是平行四边形
理由:∵△DCE绕点D顺时针旋转90°得到△DAE′
∴CE=AE′,∵CG=CE,∴CG=AE′,∵AB=CD,AB∥CD,
∴BE′=DG,BE′∥DG,………………6分
∴四边形E′BGD是平行四边形 ………………8分
10. .甲题:
(1)证明: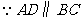
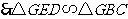 , 2分
, 2分
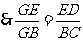 , 3分
, 3分
又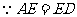 ,
,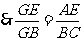 . 4分
. 4分
(2)解: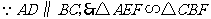
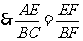 , 5分
, 5分
由(1)知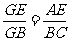 ,
,
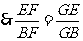 , 6分
, 6分
设 ,则
,则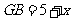 ,
,
则有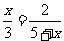 , 8分
, 8分
即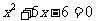 ,
,
解得: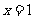 或
或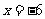 ,
,
经检验,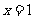 或
或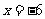 都是原方程的根,但
都是原方程的根,但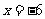 不合题意,舍去.
不合题意,舍去.
故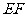 的长为1.
9分
的长为1.
9分
9. 解:(1)作图(略). 3分
注:本题作法较多,如:方法一,作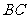 的中垂线:方法二,以
的中垂线:方法二,以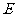 为圆心,
为圆心,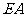 为半径画弧,交
为半径画弧,交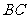 于点
于点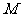 .等等.
.等等.
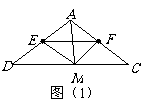 (2)如图(1),
(2)如图(1),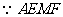 为菱形,
为菱形,
 平分
平分 , 5分
, 5分
又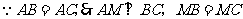 ,
,
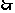 在
在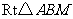 中,
中,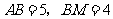 ,
,
则 , 6分
, 6分
又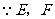 分别是
分别是 、
、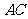 的中点,
的中点,
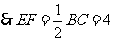 , 7分
, 7分
故菱形的面积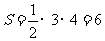 (cm2). 9分
(cm2). 9分
(我感觉此题不正确,这样能保证以E.F为圆心,以AE的长为半径的弧交点一定在BC上吗)
8. (1)解:由题意,有△BEF≌△DEF.
∴BF=DF. ……1分
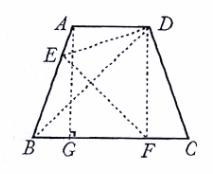 如图,过点A作AG⊥BG于点G.
如图,过点A作AG⊥BG于点G.
则四边形AGFD是矩形。
∴AG=DF,GF=AD=4.
在Rt△ABG和Rt△DCF种,
∵AB=DC,AG=DF,
∴Rt△ABG≌Rt△DCF.(HL)
∴BG=CF. ……2分
∴BG=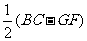 =
=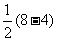 =2.
=2.
∴DF=BF=BG+GF=2+4=6. ……2分
∴S梯形ABCD=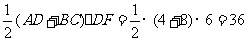 .
……1分
.
……1分
 (2)猜想:CG=
(2)猜想:CG=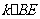 (或
(或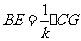 ).
……1分
).
……1分
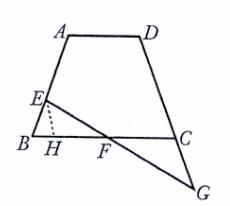
证明:如图,过点E作EH∥CG,交BC于点H.
则∠FEH=∠FGC.
又∠EFH=∠GFC,
∴△EFH∽△GFC.
∴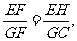
而FG=k EF,即
EF,即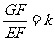 .
.
∴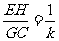 即
即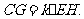 ……1分
……1分
∵EH∥CG, ∴∠EHB=∠DCB.
而ABCD是等腰梯形,∴∠B=∠DCB.
∴∠B=∠EHB.∴BE=EH. ∴CG=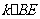 ……1分
……1分
7.(1)证明: 点
点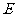 是
是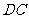 中点
中点
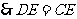 1分
1分
又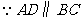 ,
,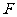 在
在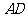 延长线上,
延长线上,
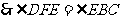 ,
,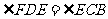 3分
3分
在 与
与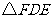 中
中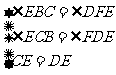 5分
5分
 6分
6分
(2)四边形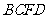 是平行四边形.理由如下: 7分
是平行四边形.理由如下: 7分
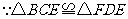
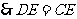 ,
,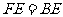 9分
9分
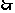 四边形
四边形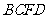 是平行四边形. 10分
是平行四边形. 10分
6. 解:(1)过点G作GH⊥AD,则四边形ABGH为矩形,∴GH=AB=8,AH=BG=10,由图形的折叠可知△BFG≌△EFG,∴EG=BG=10,∠FEG=∠B=90°;∴EH=6,AE=4,∠AEF+∠HEG=90°,∵∠AEF+∠AFE=90°,∴∠HEG=∠AFE,又∵∠EHG=∠A=90°,∴△EAF∽△EHG,∴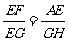 ,∴EF=5,∴S△EFG=
,∴EF=5,∴S△EFG= EF·EG=
EF·EG= ×5×10=25.
×5×10=25.
(2)由图形的折叠可知四边形ABGF≌四边形HEGF,∴BG=EG,AB=EH,
∠BGF=∠EGF,∵EF∥BG,∴∠BGF=∠EFG,∴∠EGF =∠EFG,∴EF=EG,
∴BG=EF,∴四边形BGEF为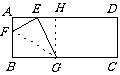
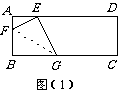 平行四边形,又∵EF=EG,∴平行四边形BGEF为菱形
平行四边形,又∵EF=EG,∴平行四边形BGEF为菱形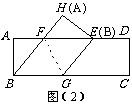 ;
;
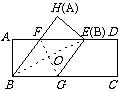 连结BE,BE、FG互相垂直平分,在Rt△EFH中,EF=BG=10,EH=AB=8,由勾股定理可得FH=AF=6,∴AE=16,∴BE=
连结BE,BE、FG互相垂直平分,在Rt△EFH中,EF=BG=10,EH=AB=8,由勾股定理可得FH=AF=6,∴AE=16,∴BE=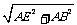 =8
=8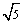 ,∴BO=4
,∴BO=4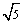 ,∴
,∴
FG=2OG=2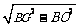 =4
=4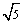 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com