
(七)转化思想
数学问题的求解过程,实际上就是问题的转化过程。它主要体现在条件由“隐”转化为“显”,结论由“暗”转化为“明”,即从陌生向熟悉、复杂向简单、间接向直接的过程。
[例7] 设圆满足:① 截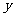 轴所得弦长为2;② 被
轴所得弦长为2;② 被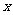 轴分成两段圆弧,其弧长的比为
轴分成两段圆弧,其弧长的比为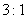 ,在满足条件①、②的所有圆中,求圆心到直线
,在满足条件①、②的所有圆中,求圆心到直线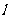 :
: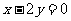 的距离最小的圆的方程。
的距离最小的圆的方程。
解:设圆的圆心为P( ),半径为
),半径为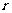 ,由①知
,由①知 ;由②知,圆P截
;由②知,圆P截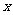 轴所得劣弧对应的圆心角为
轴所得劣弧对应的圆心角为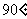 ,即圆P截
,即圆P截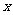 轴所得的弦长为
轴所得的弦长为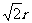 ,故有
,故有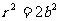 ,消去
,消去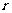 得圆心的轨迹为:
得圆心的轨迹为: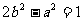
如何求圆心P( )到直线
)到直线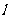 :
: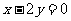 的距离
的距离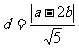 的最小值,这样转化为从不同角度求条件最值问题。
的最小值,这样转化为从不同角度求条件最值问题。
转化1:变量替换求最值
∵ 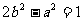 ∴
∴ 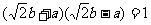
设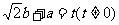 ,则有
,则有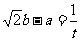 ,解得
,解得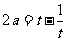 ,
,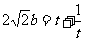 ,所以有
,所以有
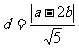
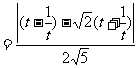 =
=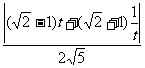
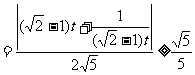
当且仅当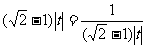 ,即
,即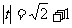 时,
时,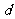 达到最小值。此时可求得
达到最小值。此时可求得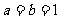 或
或
由于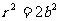 ,故
,故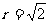 。于是所求圆的方程是:
。于是所求圆的方程是:
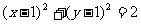 或
或
转化2:三角代换求最值
令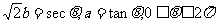 ,
,
则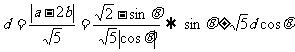
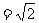 ,
,
所以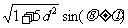
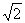
由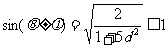 ,得
,得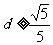
当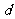 达到最小值
达到最小值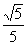 时,
时,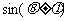 =1,从而
=1,从而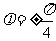 ,并由此解得
,并由此解得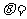
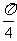 或
或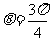
即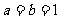 或
或 ,以下同解法1
,以下同解法1
转化3:判别式法求最值
由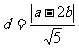 得
得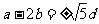 ,即
,即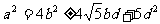 ①
①
将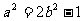 代入①式,整理得
代入①式,整理得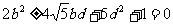 ②
②
把它看作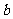 的一元二次方程,由于方程有实根,故判别式非负,即
的一元二次方程,由于方程有实根,故判别式非负,即
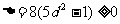 ,得
,得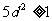 ,所以
,所以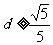
将 代入②,得
代入②,得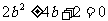
解得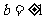
从而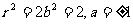 ,由
,由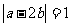 ,知
,知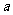 与
与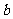 同号
同号
于是,所求圆的方程为: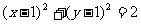 或
或
[模拟试题](答题时间:60分钟)
1. 已知椭圆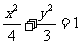 ,能否在此椭圆位于
,能否在此椭圆位于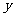 轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点
轴左侧的部分上找到一点M,使它到左准线的距离为它到两焦点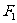 、
、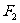 距离的等比中项?
距离的等比中项?
2. 求证:椭圆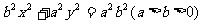 的弦中点与椭圆中心连线的斜率(两斜率均存在时)与此弦的斜率之积为
的弦中点与椭圆中心连线的斜率(两斜率均存在时)与此弦的斜率之积为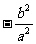 。
。
3. 一椭圆长短轴平行于坐标轴,与直线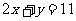 相切于点P(4,3),它还经过点Q(
相切于点P(4,3),它还经过点Q(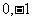 ),R(
),R(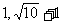 ),求椭圆方程。
),求椭圆方程。
4. 两个不同的点P、Q在曲线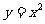 上移动,不管如何选择其位置,它们总不能关于直线
上移动,不管如何选择其位置,它们总不能关于直线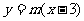 对称,求
对称,求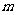 的范围。
的范围。
5. 过抛物线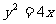 的焦点F的直线
的焦点F的直线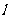 与该抛物线交于A、B两点,若AB的中点为M,直线
与该抛物线交于A、B两点,若AB的中点为M,直线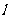 的斜率为
的斜率为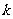 。
。
(1)试用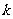 表示点M的坐标;
表示点M的坐标;
(2)若直线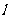 的斜率
的斜率 ,且点M到直线
,且点M到直线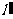 :
: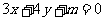 的距离为
的距离为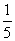 ,试确定实数
,试确定实数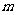 的取值范围。
的取值范围。
6. 已知椭圆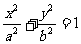 (
(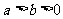 ),A、B是椭圆上两点,线段AB的垂直平分线与
),A、B是椭圆上两点,线段AB的垂直平分线与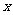 轴交于点P(
轴交于点P(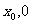 ),求证:
),求证: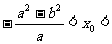
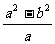 。
。
(六)参数思想
处理圆锥曲线问题,可以通过引入参变量替换,使许多相关或不相关的量统一在参变量下,其妙处在于减少未知量的个数或转化原命题的结构,以达到简化解题过程的目的。
[例6] 当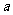 为何实数时,椭圆
为何实数时,椭圆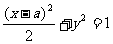 与曲线C:
与曲线C: 有公共点?
有公共点?
解:椭圆方程变形为: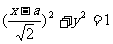
设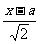
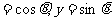 ,即
,即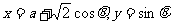 代入曲线C得:
代入曲线C得:
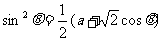 ,即
,即 (1)
(1)
椭圆与曲线C有交点,等价于方程(1)有解,即等价于函数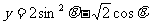 的值域
的值域
所以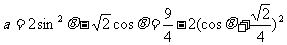
因为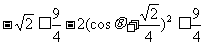 ,所以
,所以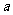 的取值范围是
的取值范围是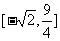
(五)函数思想
对于圆锥曲线问题上一些动点,在变化过程中会引入一些相互联系、相互制约的变量,从而使变量与其中的参变量之间构成函数关系,此时,用函数思想与函数方法处理起来十分方便。
[例5] 直线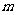 :
: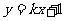 和双曲线
和双曲线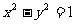 的左支交于A、B两点,直线
的左支交于A、B两点,直线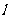 过P(
过P(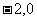 )和AB线段的中点M,求
)和AB线段的中点M,求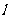 在
在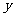 轴上的截距
轴上的截距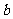 的取值范围。
的取值范围。
解:由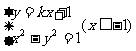 消去
消去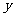 得
得 ,由题意,有:
,由题意,有:

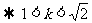
设M( ),则
),则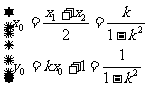
由P(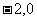 )、M(
)、M(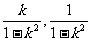 )、Q(
)、Q( )三点共线,可求得
)三点共线,可求得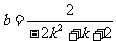
设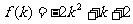
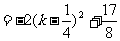 ,则
,则 在
在 上为减函数。
上为减函数。
所以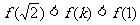 ,且
,且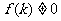
所以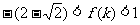 所以
所以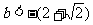 或
或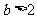
(四)方程思想
把圆锥曲线问题中的解析式看作一个方程,通过解方程的手段或对方程的研究,使问题得到解决,这种思想方法在解析几何试题中经常使用。
[例4] 已知双曲线C: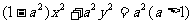 ,设该双曲线上支的顶点为A,且上支与直线
,设该双曲线上支的顶点为A,且上支与直线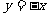 相交于P点,一条以A为焦点,M(
相交于P点,一条以A为焦点,M(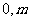 )为顶点,开口向下的抛物线通过点P,设PM的斜率为
)为顶点,开口向下的抛物线通过点P,设PM的斜率为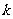 ,且
,且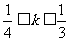 ,求实数
,求实数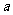 的取值范围。
的取值范围。
解:由双曲线方程知A(0,1),则抛物线方程为 ,由双曲线与直线相交,解得点P的坐标为
,由双曲线与直线相交,解得点P的坐标为 ,又因为点P在抛物线上,所以
,又因为点P在抛物线上,所以
 ①
①
而MP的斜率为 ,所以
,所以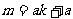
将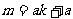 代入①,得
代入①,得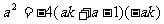 ,即
,即 ②
②
根据题意,方程②在区间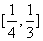 上有实根
上有实根
令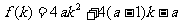 ,其对称轴方程为
,其对称轴方程为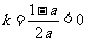
所以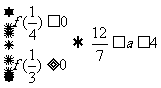 所以实数
所以实数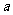 的取值范围为
的取值范围为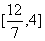
(三)整体思想
对有些圆锥曲线问题,注意其整体结构特点,设法将问题整体变形转化,以达到避免一些不必要的运算,降低解题难度。
[例3] 从椭圆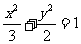 外一点P(2,4)作椭圆的切线,求两切线的夹角。
外一点P(2,4)作椭圆的切线,求两切线的夹角。
解:由椭圆的切线方程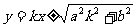 知两切线的方程为:
知两切线的方程为: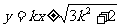
又切线过点P(2,4),所以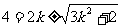 ,整理得,
,整理得,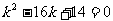
所以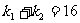 ,
,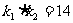
所以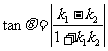
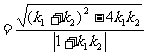
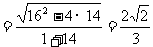
所以两切线的夹角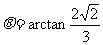
(二)补集思想
有些圆锥曲线问题,从正面处理较难,常需分类讨论,运算量大,且讨论不全又容易出错,如用补集思想考虑其对立面,可以达到化繁为简的目的。
[例2] 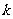 为何值时,直线
为何值时,直线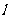 :
: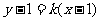 不能垂直平分抛物线
不能垂直平分抛物线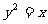 的某弦。
的某弦。
解:设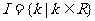 ,
,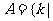 直线
直线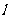 垂直平分抛物线
垂直平分抛物线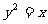 的某弦
的某弦 。若直线
。若直线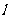 垂直平分抛物线的弦AB,且A
垂直平分抛物线的弦AB,且A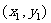 ,B
,B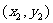 ,则
,则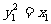 ,
,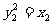
上述两式相减得: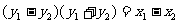
即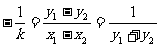
又设M是弦AB的中点,且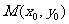 ,则
,则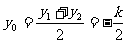
因为点M在直线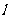 上,所以
上,所以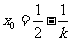
由于M在抛物线的内部,所以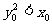 ,即
,即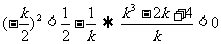
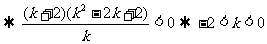
故原命题中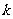 的取值范围是
的取值范围是 或
或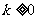
(一)极端思想
通过考察圆锥曲线问题的极端元素,灵活地借助极限状态解题,则可以避开抽象及复杂运算,优化解题过程,降低解题难度。这是简化运算量的一条重要途径。
[例1] 求已知离心率 ,过点(1,0)且与直线
,过点(1,0)且与直线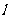 :
: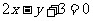 相切于点(
相切于点(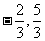 ),长轴平行于
),长轴平行于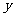 轴的椭圆方程。
轴的椭圆方程。
解:把点(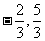 )看作离心率
)看作离心率 的椭圆
的椭圆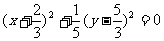 (“点椭圆”),则与直线
(“点椭圆”),则与直线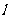 :
: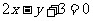 相切于该点的椭圆系即为过直线
相切于该点的椭圆系即为过直线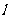 与“点椭圆”的公共点的椭圆系方程为:
与“点椭圆”的公共点的椭圆系方程为: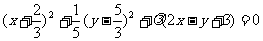
又由于所求的椭圆过点(1,0),代入上式得,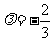
因此,所求椭圆方程为:
1. 重点:
圆锥曲线的综合问题。
2. 难点:
灵活运用介绍的几种数学思想简化圆锥曲线的运算。
[典型例题]
专题(一)简化圆锥曲线运算的几种数学思想
22、(本题满分12分)
已知在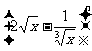 的展开式中,第二项的二项式系数与第三项的二项式系数之比为2∶9.
的展开式中,第二项的二项式系数与第三项的二项式系数之比为2∶9.
(1) 求n的值.
(2) 求展开式中所有项的系数之和.
(3) 求展开式中的常数项.
云南省玉溪市华培外语实验学校高二下学期第二次月考
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com