
8. 不等式log (x
(x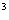 +x+3)>log
+x+3)>log (x+2)的解是____________。
(x+2)的解是____________。
7. 函数y= +
+ 的值域是____________。
的值域是____________。
6. 已知点M(3cosx,3sinx)、N(4cosy,4siny),则|MN|的最大值为_________。
5. 已知长方体ABCD-A’B’C’D’中,AA’=AD=1,AB= ,则顶点A到截面A’BD的距离是_______。
,则顶点A到截面A’BD的距离是_______。
4. (a+b+c)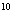 展开式的项数是_____。
展开式的项数是_____。
A. 11 B. 66
C. 132 D. 3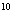
3.  [
[ -
- ] (n∈N)的值为______。
] (n∈N)的值为______。
A.  B.
B.  C. 0 D. 1
C. 0 D. 1
2. 函数f(x)=|lgx|,若0<a<b时有f(a)>f(b),则下列各式中成立的是_____。
A. ab≤1 B. ab<1 C. ab>1 D. a>1且b>1
1. 正方形ABCD与正方形ABEF成90°的二面角,则AC与BF所成的角为_____。
A. 45° B. 60° C. 30° D. 90°
6. 已知三棱锥S-ABC的三条侧棱两两垂直,SA=5,SB=4,SC=3,D为AB的中点,E为AC的中点,则四棱锥S-BCED的体积为_____。
A.  B. 10 C.
B. 10 C.  D.
D. 
[简解]1小题:由已知转化为周期为2,所以f(7.5)=f(-0.5)=-f(0.5),选B;
2小题:设f(x)=y,由互为反函数的值域与定义域的关系,选C;
3小题:由mp+nq≤ +
+ 容易求解,选A;
容易求解,选A;
4小题:由复数模几何意义利用数形结合法求解,选A;
5小题:ab= ×
× ,变形为12e
,变形为12e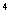 -31e
-31e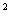 +7=0,再解出e,选B;
+7=0,再解出e,选B;
6小题:由S =
= S
S 和三棱椎的等体积转化容易求,选A。
和三棱椎的等体积转化容易求,选A。
Ⅱ、示范性题组:
例1. 若x、y、z∈R 且x+y+z=1,求(
且x+y+z=1,求( -1)(
-1)(  -1)(
-1)(  -1)的最小值。
-1)的最小值。
[分析]由已知x+y+z=1而联想到,只有将所求式变形为含代数式x+y+z,或者运用均值不等式后含xyz的形式。所以,关键是将所求式进行合理的变形,即等价转化。
[解]( -1)(
-1)(  -1)(
-1)(  -1)=
-1)= (1-x)(1-y)(1-z)
(1-x)(1-y)(1-z)
= (1-x-y-z+xy+yz+zx-xyz)=
(1-x-y-z+xy+yz+zx-xyz)= (xy+yz+zx-xyz)
(xy+yz+zx-xyz)
=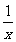 +
+ +
+ -1≥3
-1≥3 -1=
-1= -1≥
-1≥ -1=9
-1=9
[注]对所求式进行等价变换:先通分,再整理分子,最后拆分。将问题转化为求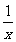 +
+ +
+ 的最小值,则不难由平均值不等式而进行解决。此题属于代数恒等变形题型,即代数式在形变中保持值不变。
的最小值,则不难由平均值不等式而进行解决。此题属于代数恒等变形题型,即代数式在形变中保持值不变。
例2. 设x、y∈R且3x +2y
+2y =6x,求x
=6x,求x +y
+y 的范围。
的范围。
[分析]
设k=x +y
+y ,再代入消去y,转化为关于x的方程有实数解时求参数k范围的问题。其中要注意隐含条件,即x的范围。
,再代入消去y,转化为关于x的方程有实数解时求参数k范围的问题。其中要注意隐含条件,即x的范围。
[解]由6x-3x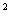 =2y
=2y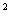 ≥0得0≤x≤2。
≥0得0≤x≤2。
设k=x +y
+y ,则y
,则y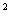 =k-x
=k-x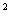 ,代入已知等式得:x
,代入已知等式得:x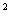 -6x+2k=0 ,
-6x+2k=0 ,
即k=- x
x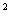 +3x,其对称轴为x=3。
+3x,其对称轴为x=3。
由0≤x≤2得k∈[0,4]。
所以x +y
+y 的范围是:0≤x
的范围是:0≤x +y
+y ≤4。
≤4。
[另解] 数形结合法(转化为解析几何问题):
由3x +2y
+2y =6x得(x-1)
=6x得(x-1)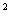 +
+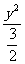 =1,即表示如图所示椭圆,其一个顶点在坐标原点。x
=1,即表示如图所示椭圆,其一个顶点在坐标原点。x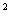 +y
+y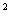 的范围就是椭圆上的点到坐标原点的距离的平方。由图可知最小值是0,距离最大的点是以原点为圆心的圆与椭圆相切的切点。设圆方程为x
的范围就是椭圆上的点到坐标原点的距离的平方。由图可知最小值是0,距离最大的点是以原点为圆心的圆与椭圆相切的切点。设圆方程为x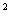 +y
+y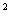 =k,代入椭圆中消y得x
=k,代入椭圆中消y得x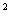 -6x+2k=0。由判别式△=36-8k=0得k=4,所以x
-6x+2k=0。由判别式△=36-8k=0得k=4,所以x +y
+y 的范围是:0≤x
的范围是:0≤x +y
+y ≤4。
≤4。
[再解] 三角换元法,对已知式和待求式都可以进行三角换元(转化为三角问题):
由3x +2y
+2y =6x得(x-1)
=6x得(x-1)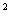 +
+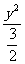 =1,设
=1,设 ,则
,则
x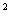 +y
+y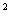 =1+2cosα+cos
=1+2cosα+cos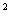 α+
α+ sin
sin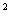 α=1+
α=1+ +2cosα-
+2cosα- cos
cos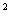 α
α
=- cos
cos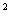 α+2cosα+
α+2cosα+ ∈[0,4]
∈[0,4]
所以x +y
+y 的范围是:0≤x
的范围是:0≤x +y
+y ≤4。
≤4。
[注]本题运用多种方法进行解答,实现了多种角度的转化,联系了多个知识点,有助于提高发散思维能力。此题还可以利用均值换元法进行解答。各种方法的运用,分别将代数问题转化为了其它问题,属于问题转换题型。
例3. 求值:ctg10°-4cos10°
[分析]分析所求值的式子,估计两条途径:一是将函数名化为相同,二是将非特殊角化为特殊角。
[解一]ctg10°-4cos10°= -4cos10°=
-4cos10°=
= =
=
= =
= =
= =
=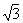
(基本过程:切化弦→通分→化同名→拆项→差化积→化同名→差化积)
[解二]ctg10°-4cos10°= -4cos10°=
-4cos10°=
= =
=
= =
=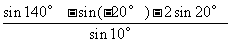
= =
= =
=
(基本过程:切化弦→通分→化同名→特值代入→积化和→差化积)
[解三]ctg10°-4cos10°= -4cos10°=
-4cos10°=
= =
=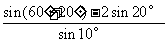
= =
=
= =
=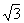
(基本过程:切化弦→通分→化同名→拆角80°→和差角公式)
[注]无条件三角求值问题,是高考中常见题型,其变换过程是等价转化思想的体现。此种题型属于三角变换型。一般对,对于三角恒等变换,需要灵活运用的是同角三角函数的关系式、诱导公式、和差角公式、倍半角公式、和积互化公式以及万能公式,常用的手段是:切割化弦、拆角、将次与升次、和积互化、异名化同名、异角化同角、化特殊角等等。对此,我们要掌握变换的通法,活用2公式,攻克三角恒等变形的每一道难关。
例4. 已知f(x)=tgx,x∈(0,  ),若x
),若x 、x
、x ∈(0,
∈(0,  )且x
)且x ≠x
≠x ,
,
求证: [f(x
[f(x )+f(x
)+f(x )]>f(
)]>f( )
(94年全国高考)
)
(94年全国高考)
[分析]从问题着手进行思考,运用分析法,一步步探求问题成立的充分条件。
[证明] [f(x
[f(x )+f(x
)+f(x )]>f(
)]>f( )
) 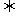
 [tgx
[tgx +tgx
+tgx ]>tg
]>tg
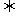
 (
( +
+ )>
)>
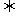

 >
>
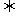 1+cos(x
1+cos(x +x
+x )>2cosx
)>2cosx cosx
cosx
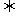 1+cosx
1+cosx cosx
cosx +sinx
+sinx sinx
sinx >2cosx
>2cosx cosx
cosx
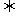 cosx
cosx cosx
cosx +sinx
+sinx sinx
sinx <1
<1 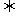 cos(x
cos(x -x
-x )<1
)<1
由已知显然cos(x -x
-x )<1成立,所以
)<1成立,所以 [f(x
[f(x )+f(x
)+f(x )]>f(
)]>f( )
)
      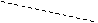     S
A
M S
A
M
D N C B |
[注] 本题在用分析法证明数学问题的过程中,每一步实施的都是等价转化。此种题型属于分析证明型。
例5. 如图,在三棱锥S-ABC中,S在底面上的射影N位于底面的高CD上,M是侧棱SC上的一点,使截面MAB与底面所成角等于∠NSC。求证:SC垂直于截面MAB。(83年全国高考)
[分析] 由三垂线定理容易证明SC⊥AB,再在平面SDNC中利用平面几何知识证明SC⊥DM。
[证明]由已知可得:SN⊥底面ABC,AB⊥CD,CD是斜线SC在底面AB的射影,
∴ AB⊥SC。
∵ AB⊥SC、AB⊥CD
∴ AB⊥平面SDNC
∴ ∠MDC就是截面MAB与底面所成的二面角
由已知得∠MDC=∠NSC
又∵ ∠DCM=∠SCN
∴ △DCM≌△SCM
∴ ∠DMC=∠SNC=Rt∠
即 SC⊥DM
所以SC⊥截面MAB。
[注]立体几何中有些问题的证明,可以转化为平面几何证明来解决,即考虑在一个平面上的证明时运用平面几何知识。
Ⅲ、巩固性题组:
5. 设椭圆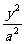 +
+ =1 (a>b>0)的半焦距为c,直线l过(0,a)和(b,0),已知原点到l的距离等于
=1 (a>b>0)的半焦距为c,直线l过(0,a)和(b,0),已知原点到l的距离等于 c,则椭圆的离心率为_____。
c,则椭圆的离心率为_____。
A.  B.
B.  C.
C.  D.
D.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com