
3.(2006辽宁)函数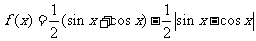 ,的值域是 ( )
,的值域是 ( )
(A)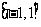 (B)
(B) 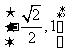 (C)
(C) 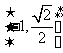 (D)
(D) 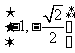
2.(05全国卷Ⅱ)已知函数 内是减函数,则 ( )
内是减函数,则 ( )
A.0<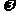 ≤1 B.-1≤
≤1 B.-1≤ <0 C.
<0 C. ≥1 D.
≥1 D.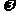 ≤-1
≤-1
1.(2006福建9)已知函数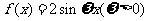 在区间
在区间 上的最小值是
上的最小值是 ,则
,则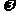 的最小值等于
( )
的最小值等于
( )
(A)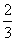 (B)
(B)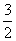 (C)2 (D)3
(C)2 (D)3
3.要善于运用图象解题,数形结合,数形转化。
同步练习 4.5 三角函数的图象和性质
[选择题]
2.设参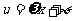 可以帮助理解,熟练了以后可以省却这个过程.
可以帮助理解,熟练了以后可以省却这个过程.
1.熟记三角函数的图象与各性质很重要.
[例1](2003春北京)已知函数f(x)=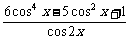 ,求f(x)的定义域,判断它的奇偶性,并求其值域.
,求f(x)的定义域,判断它的奇偶性,并求其值域.
解:由cos2x≠0得2x≠kπ+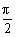 ,解得x≠
,解得x≠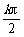 +
+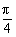 (k∈Z).
(k∈Z).
所以f(x)的定义域为{x|x∈R且x≠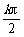 +
+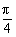 ,k∈Z}.
,k∈Z}.
因为f(x)的定义域关于原点对称,且
f(-x)=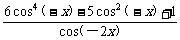
=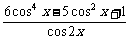 =f(x),
=f(x),
所以f(x)是偶函数.
又当x≠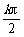 +
+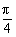 (k∈Z)时,
(k∈Z)时,
f(x)=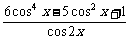
=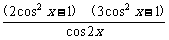 =3cos2x-1=
=3cos2x-1=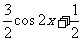 ,
,
所以f(x)的值域为{y|-1≤y<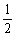 或
或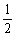 <y≤2}.
<y≤2}.
◆提炼方法:对复杂的函数式,要先化简为Asin(ωx+φ)+m,或Acos(ωx+φ)+m的形式,再讨论性质.
[例2] 锐角x、y满足sinycscx=cos(x+y)且x+y≠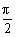 ,求tany的最大值.和取最大值时角x的集合.
,求tany的最大值.和取最大值时角x的集合.
解:∵sinycscx=cos(x+y),
∴sinycscx=cosxcosy-sinxsiny,
siny(sinx+cscx)=cosxcosy.
∴tany=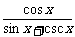 =
=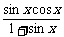 =
=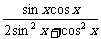 =
= ≤
≤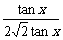 =
=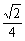 ,
,
当且仅当tanx= 时取等号.
时取等号.
∴tany的最大值为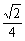 .对应角x的集合为
.对应角x的集合为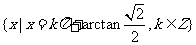
◆ 提炼方法:先由已知变换出tany与x的函数关系,再用不等式求最值;是三角、函数、不等式知识的综合应用。
[例3](2006辽宁)已知函数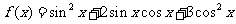 ,
,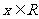 .求:
.求:
(I)函数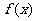 的最大值及取得最大值的自变量
的最大值及取得最大值的自变量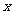 的集合;
的集合;
(II)函数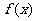 的单调增区间.
的单调增区间.
(I)解法一:
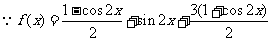
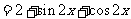
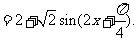
∴当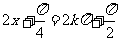 ,即
,即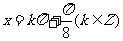 时,
时,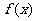 取得最大值
取得最大值
因此,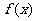 取得最大值的自变量
取得最大值的自变量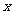 的集合是
的集合是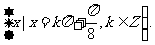
解法二: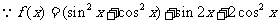
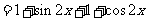
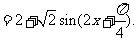
∴当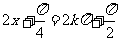 ,即
,即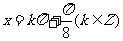 时,
时,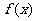 取得最大值
取得最大值
因此,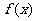 取得最大值的自变量
取得最大值的自变量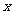 的集合是
的集合是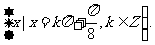
(II)解: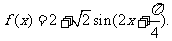
由题意得 ,
,
即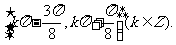
因此,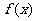 的单调增区间是
的单调增区间是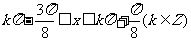
[例4]是否存在实数a,使得函数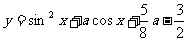 在闭区间
在闭区间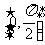 上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由。
上的最大值是1?若存在,求出对应的a值?若不存在,试说明理由。
解: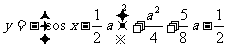
当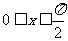 时,
时,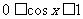 ,令
,令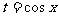 则
则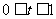 ,
,
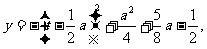
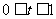
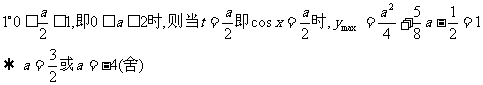

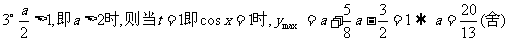
综上知,存在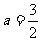 符合题意。
符合题意。
◆思维点拨:化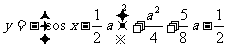 ,闭区间上的二次函数的最值问题字母分类讨论思路。
,闭区间上的二次函数的最值问题字母分类讨论思路。
[研讨.欣赏](2003江苏)已知函数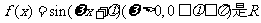 上的偶函数,其图象关于点
上的偶函数,其图象关于点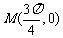 对称,且在区间
对称,且在区间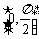 上是单调函数.求
上是单调函数.求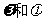 的值。
的值。
解:由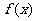 是偶函数,得
是偶函数,得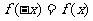 ,即
,即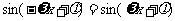 ,
,
所以 ,
,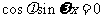
对任意x都成立,且 ,所以得
,所以得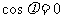 ,
,
依题设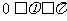 ,所以解得
,所以解得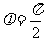 .
.
由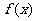 的图象关于点M对称,得
的图象关于点M对称,得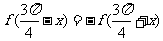 ,
,
取 得
得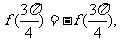 所以
所以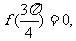
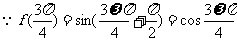 ,
,
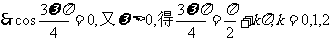 …,
…,
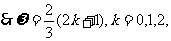 ….
….
当k=0时,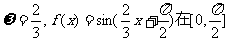 上是减函数;
上是减函数;
当k=1时,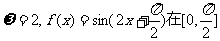 上是减函数;
上是减函数;
当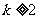 时,
时,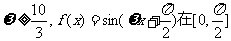 上不是单调函数.
上不是单调函数.
所以,综合得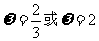 .
.
6.化为一个角的三角数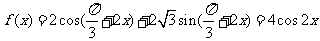 周期是π; 7. 答案:④
周期是π; 7. 答案:④
5.49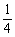 ×T≤1,即
×T≤1,即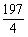 ×
×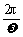 ≤1,∴ω≥
≤1,∴ω≥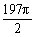 .答案
.答案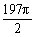
思考:若条件改为在[x0,x0+1]上至少出现50次最大值呢?
4. y=sin2α-sinα+1=(sinα-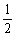 )2+
)2+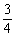 .
.
∵ cosβ=1-sinα.∴ sinα∈[0,1]∴y∈[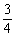 ,1].
,1].
(本题易错解为y=sin2α+1-sinα,sinα∈[-1,1],求y的取值范围.)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com