
27. 证明: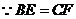 ,
,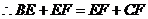 ,
,
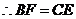 ·················································································································· 1分
·················································································································· 1分
在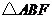 与
与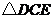 中
中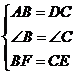
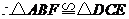 ·········································· 2分
·········································· 2分
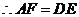
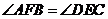
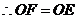 ································································ 1分
································································ 1分
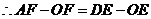
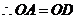 1分
1分
26. 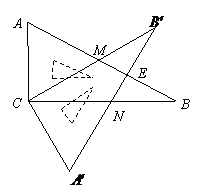 (1) 证明:∵∠A=∠A′ AC=A′C ∠ACM=∠A′CN=900-∠MCN
(1) 证明:∵∠A=∠A′ AC=A′C ∠ACM=∠A′CN=900-∠MCN
∴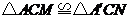
(2)在Rt△ABC中
∵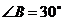 ,∴∠A=900-300=600
,∴∠A=900-300=600
又∵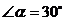 ,∴∠MCN=300,
,∴∠MCN=300,
∴∠ACM=900-∠MCN=600
∴∠EMB′=∠AMC=∠A=∠MCA=600
∵∠B′=∠B=300
所以三角形MEB′是Rt△MEB′且∠B′=300
所以MB′=2ME
25. 证明:(1)∵CF∥BE∴EBD=FCD
又∵∠BDE=∠CDF,BD=CD
∴△BDE≌△CDF
(2)四边形BECF是平行四边形
由△BDE≌△CDF得ED=FD
∵BD=CD
∴四边形BECF是平行四边形
24. (1)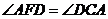 (或相等)
(或相等)
(2)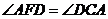 (或成立),理由如下
(或成立),理由如下
方法一:由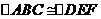 ,得
,得
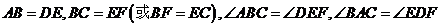
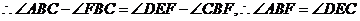
在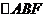 和
和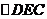 中
中
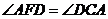
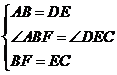
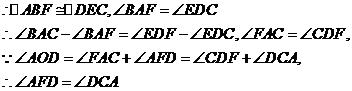
方法二、连接AD,同方法一,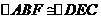 ,所以AF=DC。
,所以AF=DC。
由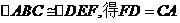 。可证
。可证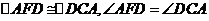 。
。
(3)如图,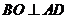
方法一:由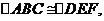 点B与点E重合,得
点B与点E重合,得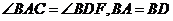 ,
,
所以点B在AD的垂直平分线上,
且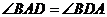
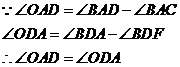
所以OA=OD,点O在AD的垂直平分线上,故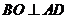 。
。
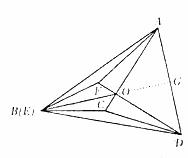
方法二:延长BO交AD于点G。同方法一OA=OD,可证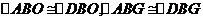
则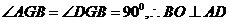 。
。
23. (1)解:图2中△ABE≌C△ACD
证明如下:
∵△ABC与AED均为等腰直角三角形
∴AB=AC ,AE=AD, ∠BAC=∠EAD=90°………………3分
∴∠BAC+∠CAE=∠EAD+∠CAE
即∠BAE=∠CAD ………………4分
∴△ABE≌△ACD………………6分
(2)证明:由(1)△ABE≌△ACD知
∠ACD=∠ABE=45°………………7分
又∠ACB=45°
∴∠BCD=∠ACB+∠ACD=90°
∴DC⊥BE………………9分
22.
[证](1)过点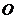 分别作
分别作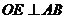 ,
,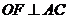 ,
,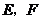 分别是垂足,由题意知,
分别是垂足,由题意知,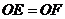 ,
,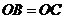 ,
,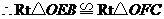 ,
,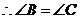 ,从而
,从而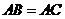 .
.
(2)过点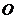 分别作
分别作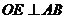 ,
,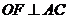 ,
,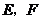 分别是垂足,
分别是垂足,
由题意知,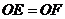 .在
.在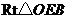 和
和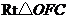 中,
中,
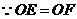 ,
,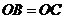 ,
,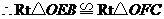 .
.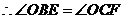 ,
,
又由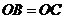 知
知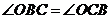 ,
,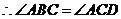 ,
,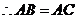 .
.
解:(3)不一定成立.
21. 证明: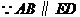 ,
,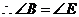 .
.
在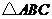 和
和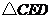 中,
中,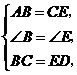
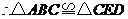 .
.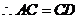 .
.
20. 证明: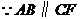 ,
,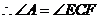 (2分)
(2分)
又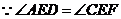 ,
,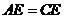 ,
,
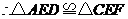 .(5分)
.(5分)
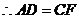 . (6分)
. (6分)
19. 证明:∵∠QAP=∠BAC
∴∠QAP+∠PAB=∠PAB+∠BAC
即∠QAB=∠PAC
在△ABQ和△ACP中
AQ=AP
∠QAB=∠PAC
AB=AC
18. 证明: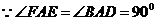
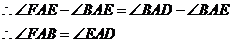
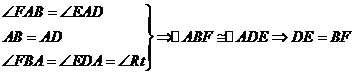
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com