（1）若CF =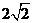AF，求E点的坐标；

（2）连结BD并延长交AF的延长线于点G，连结EG，求证：EG⊥AB；

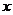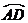26．（本题15分）如图，在直角坐标系中，⊙O交轴于A、B两点，交轴于C、D两点，A（－4，0），F为上一点，CF交AO于点E.

25．（本题12分）如图，已知平面直角坐标系中，点A（－1，a）、B（3，b）为两动点，其中A点在第二象限，B点在第一象限，以AB为直径画⊙M恰好经过O点.

（1）求证：ab = 3；

（2）是否存在实数a、b，使得△AOB的面积等于3，若存在，求a、b的值；若不存在，请说明理由.

24．（本题10分）西部建设中，某工程队承包了一段72千米的铁轨的铺设任务，计划若干天完成，在铺设完一半后，增添工作设备，改进了工作方法，这样每天比原计划可多铺3千米，结果提前了2天完成任务。若按原计划操作，每天需各种费用1万元，而改进技术后每天需各种费用1. 2万元，问实际操作中，可比原计划节约多少元？

23．（本题10分）如图，已知⊙O中，BC是直径，D点为OB上任意一点（异于O、B），过D点作AD⊥BC，交⊙O于点A。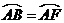，连结BF交AD于E点。

（1）探究AE与BE的大小关系，并证明你的结论；

（2）当D为OC上任意一点（异于O、C），其它条件不变时，（1）中的结论是否仍然成立，画出图形并证明你的结论。

（2）某著名跳水运动员能在0. 2秒内完成一个动作，并且在距水面3. 6米处开始入水准备不能做动作，那么该跳水运动员在10米高台跳水中能否完成5个动作？为什么？

22．（本题10分）实验得知：跳水运动员跳下的高度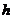（米）与所用的时间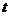（秒）之间的函数关系式为：.

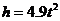（1）若跳水运动员从10米高台上跳下，求跳水运动员从起跳到入水所用的时间；