
1.根据拼音写汉字,并纠正句中的错别字。(2分)
青藏铁路建成通车,“神舟六号”宇宙飞船成功发射,三峡工程胜利浚工,被yù为21世纪的惊世壮举。
①yù ② 改为
 (3)假设点C与点F的距离为x,△DEF与△ABC重叠部分的面积为y,求y与x的函数解析式,并写出它的定义域.
(3)假设点C与点F的距离为x,△DEF与△ABC重叠部分的面积为y,求y与x的函数解析式,并写出它的定义域.
25.如图,在Rt△ABC中,∠C=90°,∠B=30°,BC=4.左右做平行移动的等边三角形DEF的两个顶点E、F始终在边BC上,DE、DF分别与AB相交于点G、H.当点F与点C重合时,点D恰好在斜边AB上.
(1)求△DEF的边长;
(2)在△DEF做平行移动的过程中,图中是否存在与线段CF始终相等的线段?如果存在,请指出这条线段,并加以证明;如果不存在,请说明理由;
24.已知抛物线 与x轴交于A(x1,0)和B(x2,0)两点,其中点A在点B的左边,顶点为C,与y轴交于点D,
与x轴交于A(x1,0)和B(x2,0)两点,其中点A在点B的左边,顶点为C,与y轴交于点D, .
.
(1)求m的取值范围;
(2)求以这条抛物线为图象的函数解析式;
(3)试比较∠CBD与∠ADO的大小关系,并说明理由.
五、(本大题只有1题,满分12分)
23.甲、乙两家便利店到批发站采购一批饮料,共25箱,由于两店所处的地理位置不同,因此甲店的销售价格比乙店的销售价格每箱多10元.当两店将所进的饮料全部售完后,甲店的营业额为1000元,比乙店少350元,求甲乙两店各进货多少箱饮料?
22.如图,在Rt△ABC中,∠ACB=90°,边AC的垂直平分线EF交
AC于点E,交AB于点F,BG⊥AB,交EF于点G.
求证:CF是EF与FG的比例中项.
 生人数约为
名.
生人数约为
名.
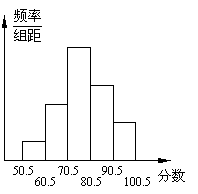 21.某校280名初三年级学生参加环保知识竞赛,随机抽取部分学生的成绩(得分取整数)进行分析,这些成绩整理后分成五组,绘制成频率分布直方图(如图),图中从左到右各小组的小长方形的高之比是1∶3∶6∶4∶2,最右边一组的频数是12.请根据所给的信息回答下列问题.
21.某校280名初三年级学生参加环保知识竞赛,随机抽取部分学生的成绩(得分取整数)进行分析,这些成绩整理后分成五组,绘制成频率分布直方图(如图),图中从左到右各小组的小长方形的高之比是1∶3∶6∶4∶2,最右边一组的频数是12.请根据所给的信息回答下列问题.
(1)抽取学生成绩的数量为 ;
(2)成绩的中位数落在 分数段中;
(3)抽样成绩超过80分的学生人数占抽样人数
的百分比是 ;
(4)由此估计这次竞赛成绩超过80分的初三学
20.如图,PA与⊙O相切于点A,PC经过圆心O,并
交⊙O于点B、C,PA=4,PB=2,求∠P的余弦值.
19.计算: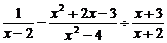 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com